Chương trình Toán 12, phần Ứng dụng hình học của tích phân đóng vai trò quan trọng trong việc củng cố kiến thức và rèn luyện kỹ năng giải toán. Tại giaitoan.edu.vn, chúng tôi cung cấp hệ thống lý thuyết đầy đủ, dễ hiểu cùng các bài tập minh họa chi tiết.
Học sinh có thể nắm vững phương pháp tính diện tích hình phẳng, thể tích khối tròn xoay và các ứng dụng thực tế khác của tích phân.
1. Tính diện tích hình phẳng Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b
1. Tính diện tích hình phẳng
Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục trên [a;b], trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \) |
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 4\), trục hoành và các đường thẳng x = -2, x = 3.
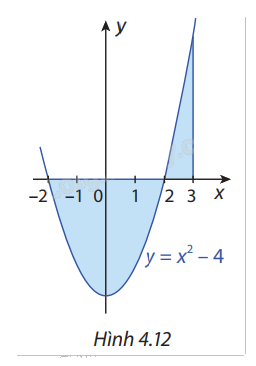
Giải:
Gọi S là diện tích hình phẳng cần tìm. Ta có:
\(S = \int\limits_{ - 2}^3 {\left| {{x^2} - 4} \right|dx} = S = \int\limits_{ - 2}^2 {\left| {{x^2} - 4} \right|dx} + S = \int\limits_2^3 {\left| {{x^2} - 4} \right|dx} \)
\(\int\limits_{ - 2}^2 {({x^2} - 4)dx} + \int\limits_2^3 {({x^2} - 4)dx} = \left( { - \frac{{{x^3}}}{3} + 4x} \right)\left| {\begin{array}{*{20}{c}}2\\{ - 2}\end{array} + } \right.\left( {\frac{{{x^3}}}{3} - 4x} \right)\left| {\begin{array}{*{20}{c}}3\\2\end{array}} \right. = 13\) (đvdt).
Hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = f(x), g(x) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng x = a, x = b được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \) |
Ví dụ: Tính diện tích hình phẳng (H) được giới hạn bởi đồ thị hai hàm số \(y = {x^2} - 2\), \(y = x\) và các đường thẳng x = -1, x= 2.
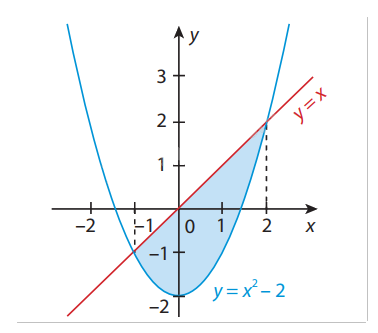
Giải:
Ta có \(x \ge {x^2} - 2\) với \(x \in [ - 1;2]\).
Diện tích hình phẳng đã cho là:
\(S = \int\limits_{ - 1}^2 {\left| {{x^2} - 2 - x} \right|dx} = \int\limits_{ - 1}^2 {\left( { - {x^2} + 2 + x} \right)dx} = \left( { - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} + 2x} \right)\left| {\begin{array}{*{20}{c}}2\\{ - 1}\end{array}} \right. = \frac{9}{2}\) (đvdt).
Chú ý:
Nếu hàm số f(x) – g(x) không đổi dấu trên đoạn [a;b] thì:
\(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} = \left| {\int\limits_a^b {\left[ {f(x) - g(x)} \right]dx} } \right|\).
2. Tính thể tích vật thể
Tính thể tích vật thể
Cho một vật thể trong không gian Oxyz. Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm x \((a \le x \le b)\) thì phần chung giữa mặt phẳng và vật thể có diện tích S(x). Giả sử S(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\). Khi đó thể tích V của vật thể B được tính bởi công thức \(V = \int\limits_a^b {S(x)dx} \) |
Ví dụ: Hãy sử dụng tích phân tính thể tích khối lăng trụ có diện tích đáy bằng S (không đổi) và chiều cao h.
Giải:
Chọn trục Ox song song với đường cao của khối lăng trụ, hai đáy nằm trong mặt phẳng vuông góc với Ox tại x= 0, x = h.
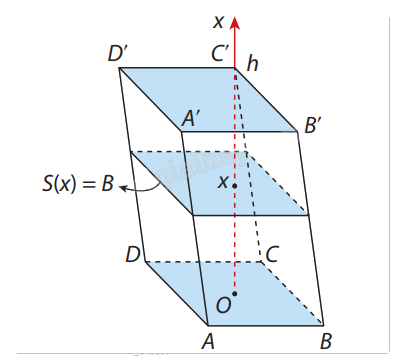
Khi cắt khối lăng trụ bởi mặt phẳng vuông góc với trục Ox tại điểm x \((a \le x \le b)\), thì phần chung giữa mặt phẳng và khối lăng trụ là một hình phẳng có diện tích\(S(x) = S\) không đổi.
Thể tích khối lăng trụ là:
\(V = \int\limits_0^h {S(x)dx} = \int\limits_0^h {Sdx} = (Sx)\left| {\begin{array}{*{20}{c}}h\\0\end{array}} \right. = Sh\) (đvdt).
Tính thể tích khối tròn xoay
Cho hàm số f(x) liên tục, không âm trên đoạn \(\left[ {a;b} \right]\). Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b quanh trục Ox là \(V = \pi \int\limits_a^b {{f^2}(x)dx} \) |
Ví dụ 1: Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường thẳng quay quanh trục hoành \(y = {x^2} - 2x\), y = 0, x = 2.
Giải:
Thể tích khối tròn xoay là:
\(V = \pi \int\limits_0^2 {{{({x^2} - 2x)}^2}dx} = \pi \int\limits_0^2 {({x^4} - 4{x^3} + 4{x^2})dx} \)
\( = \pi \left( {\frac{{{x^5}}}{5} - {x^4} + \frac{4}{3}{x^3}} \right)\left| {\begin{array}{*{20}{c}}2\\0\end{array}} \right. = \frac{{16\pi }}{{15}}\) (đvdt).
Ví dụ 2: Hình vẽ mô phòng phần bên trong của một chậu cây có dạng khối tròn xoay tạo thành khi quay một phần của đồ thị hàm số \(y = \sqrt x + \frac{3}{2}\) với \(0 \le x \le 4\) quanh trục hoành. Tính thể tích phần bên trong (dung tích) của chậu cây, biết đơn vị trên các trục Ox, Oy là decimét.
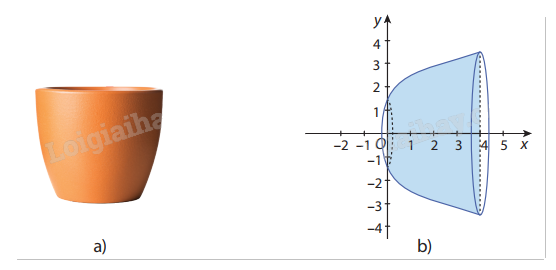
Giải:
Thể tích phần trong của chậu cây là:
\(V = \pi \int\limits_0^4 {{{\left( {\sqrt x + \frac{3}{2}} \right)}^2}dx} = \pi \int\limits_0^4 {{{\left( {x + 3{x^{\frac{1}{2}}} + \frac{9}{4}} \right)}^2}dx} = \pi \left( {\frac{{{x^2}}}{2} + 2{x^{\frac{3}{2}}} + \frac{9}{4}x} \right)\left| {\begin{array}{*{20}{c}}4\\0\end{array}} \right. = 33\pi \) (\(d{m^3}\)).
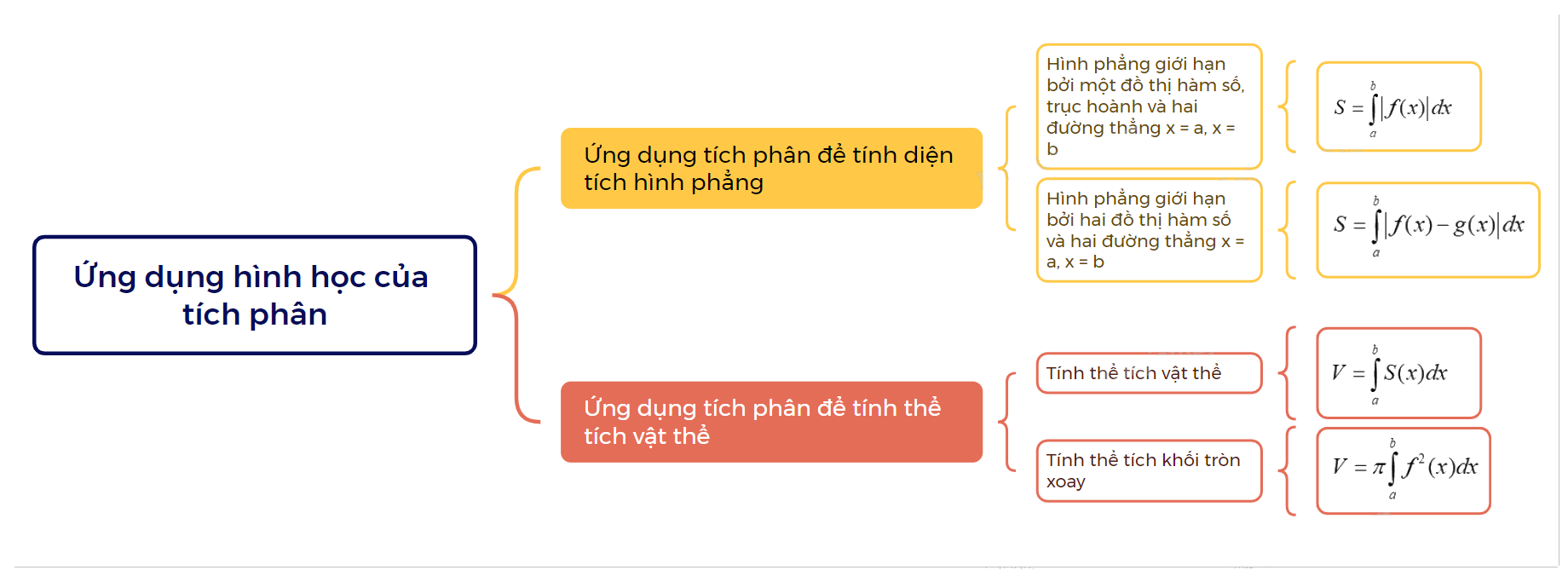
Ứng dụng hình học của tích phân là một phần quan trọng trong chương trình Toán 12, tập trung vào việc sử dụng tích phân để giải quyết các bài toán liên quan đến hình học, đặc biệt là tính diện tích hình phẳng và thể tích khối tròn xoay. Việc nắm vững kiến thức này không chỉ giúp học sinh đạt kết quả tốt trong các kỳ thi mà còn cung cấp nền tảng vững chắc cho việc học tập và nghiên cứu trong tương lai.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành Ox và hai đường thẳng x = a, x = b được tính bằng công thức:
S = ∫ab |f(x)| dx
Trong đó:
Để tính diện tích hình phẳng, cần xác định đúng các điểm giao nhau của đồ thị hàm số với trục hoành và các đường thẳng giới hạn. Sau đó, chia khoảng tích phân thành các khoảng nhỏ hơn, trên mỗi khoảng đó f(x) có dấu không đổi, và tính diện tích trên từng khoảng rồi cộng lại.
Thể tích khối tròn xoay tạo thành khi quay một hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành Ox và hai đường thẳng x = a, x = b quanh trục Ox được tính bằng công thức:
V = π ∫ab [f(x)]2 dx
Tương tự, nếu quay quanh trục Oy, công thức sẽ là:
V = π ∫cd [x(y)]2 dy
Trong đó:
Việc tính thể tích khối tròn xoay đòi hỏi học sinh phải hiểu rõ về phương pháp đĩa và phương pháp vỏ.
Các bài tập về ứng dụng hình học của tích phân thường gặp các dạng sau:
Để giải các bài tập về ứng dụng hình học của tích phân hiệu quả, cần lưu ý các mẹo sau:
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2, trục hoành Ox và đường thẳng x = 2.
Giải:
Diện tích hình phẳng là: S = ∫02 x2 dx = [x3/3]02 = 8/3
Ví dụ 2: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = √x, trục hoành Ox và đường thẳng x = 4 quanh trục Ox.
Giải:
Thể tích khối tròn xoay là: V = π ∫04 (√x)2 dx = π ∫04 x dx = π [x2/2]04 = 8π
Ứng dụng hình học của tích phân là một phần kiến thức quan trọng trong chương trình Toán 12. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập sẽ giúp học sinh tự tin đối mặt với các kỳ thi và ứng dụng kiến thức vào thực tế. Giaitoan.edu.vn hy vọng với những kiến thức và hướng dẫn trên, bạn sẽ học tập hiệu quả và đạt kết quả tốt nhất.