Chào mừng bạn đến với bài học về Lý thuyết Nguyên hàm Toán 12 tại giaitoan.edu.vn. Nguyên hàm là một khái niệm quan trọng trong giải tích, đóng vai trò then chốt trong việc giải quyết các bài toán tích phân. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan và chi tiết về lý thuyết nguyên hàm, giúp bạn nắm vững kiến thức và tự tin giải các bài tập.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, các công thức nguyên hàm cơ bản và phương pháp tìm nguyên hàm của một hàm số.
1. Khái niệm nguyên hàm
1. Khái niệm nguyên hàm
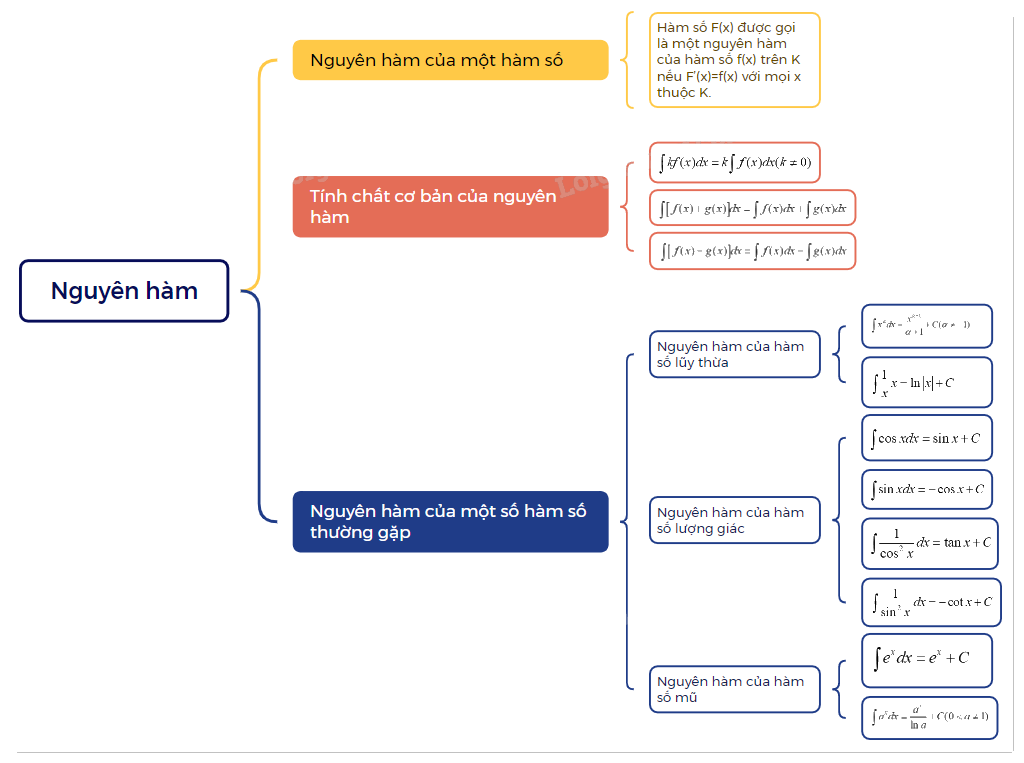
| Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K. |
Chú ý:
Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:
a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K.
b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K.
Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + với C thuộc R là họ các nguyên hàm của f(x) trên K, kí hiệu \(\int {f(x)dx} = F(x) + C\).
Ví dụ: Chứng minh \(\int {kdx} = kx + C\) với k là hằng số khác 0.
Giải:
Ta có \((kx)' = k\) nên \(F(x) = kx\) là một nguyên hàm của hàm số \(f(x) = k\).
Vậy \(\int {kdx} = kx + C\).
Nhận xét:
Ta có \(\int {0dx} = C\), \(\int {dx} = \int {1dx} = x + C\).
2. Nguyên hàm của một số hàm số thường gặp
Nguyên hàm của hàm số lũy thừa
+ \(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \) + \(\int {\frac{1}{x}x = \ln \left| x \right| + C} \) |
Ví dụ:
a) \(\int {{x^5}dx} = \frac{1}{6}{x^6} + C\).
b) \(\int {{x^{\sqrt 2 }}dx} = \frac{1}{{\sqrt 2 + 1}}{x^{\sqrt 2 + 1}} + C\).
c) \(\int {{x^{ - 1}}dx} = \int {\frac{1}{x}dx = } \ln \left| x \right| + C\).
Nguyên hàm của hàm số mũ
+ \(\int {{e^x}dx = {e^x} + C} \) + \(\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1)} \) |
Ví dụ:
a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\).
b) \(\int {{e^{3x}}dx} = \int {{{\left( {{e^3}} \right)}^x}dx} = \frac{{{{\left( {{e^3}} \right)}^x}}}{{\ln {e^3}}} + C = \frac{1}{3}{e^{3x}} + C\).
c) \(\int {{2^x}{{.3}^x}dx} = \int {{6^x}dx} = \frac{{{6^x}}}{{\ln 6}} + C\).
Nguyên hàm của hàm số lượng giác
+ \(\int {\cos xdx = \sin x + C} \) + \(\int {\sin xdx = - \cos x + C} \) + \(\int {\frac{1}{{{{\cos }^2}x}}dx = \tan x + C} \) + \(\int {\frac{1}{{{{\sin }^2}x}}dx = - \cot x + C} \) |
Ví dụ:
a) \(\int {(1 + {{\tan }^2}x)dx} = \int {\frac{1}{{{{\cos }^2}x}}dx} = \tan x + C\).
b) Tìm nguyên hàm F(x) của hàm số f(x) = sinx, biết \(F(2\pi ) = 0\).
Ta có \(\int {\sin xdx} = - \cos x + C\).
F(x) là nguyên hàm của hàm số f(x) = sinx nên có dạng F(x) = -cosx + C.
Vì \(F(2\pi ) = 0\) nên \( - \cos 2\pi + C = 0\) hay \( - 1 + C = 0\), suy ra C = 1.
Vậy F(x) = 1 – cosx.
3. Tính chất cơ bản của nguyên hàm
Nếu hai hàm số f(x) và g(x) liên tục trên K thì: + \(\int {kf(x)dx = k\int {f(x)dx(k \ne 0)} } \) + \(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \) + \(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx} } \) |
Ví dụ:
a) \(\int {6{x^3}dx} = 6\int {{x^3}dx} = 6.\frac{{{x^4}}}{4} + C = \frac{3}{2}{x^4} + C\).
b) \(\int {(3{x^2} - \cos x)dx} = 3\int {{x^2}dx} - \int {\cos xdx} = {x^3} - \sin x + C\).
c) \(\int {\left( {\frac{2}{{{{\cos }^2}x}} - {5^x}} \right)dx} = 2\int {\frac{1}{{{{\cos }^2}x}}dx} - \int {{5^x}dx} = 2\tan x - \frac{{{5^x}}}{{\ln 5}} + C\).
Nguyên hàm của một hàm số f(x) trên một khoảng I là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x) trên khoảng I. Ký hiệu: F'(x) = f(x). Nói cách khác, nguyên hàm là quá trình ngược lại của phép lấy đạo hàm.
Một hàm số f(x) có vô số nguyên hàm, chúng khác nhau bởi một hằng số cộng. Nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x), với C là một hằng số bất kỳ.
| Hàm số f(x) | Nguyên hàm F(x) |
|---|---|
| xn (n ≠ -1) | (xn+1)/(n+1) + C |
| 1/x | ln|x| + C |
| ex | ex + C |
| sin(x) | -cos(x) + C |
| cos(x) | sin(x) + C |
| 1/(1+x2) | arctan(x) + C |
Ví dụ 1: Tìm ∫x2 dx
Áp dụng công thức ∫xn dx = (xn+1)/(n+1) + C, ta có ∫x2 dx = (x3)/3 + C
Ví dụ 2: Tìm ∫sin(2x) dx
Đặt u = 2x, du = 2dx => dx = du/2. Khi đó, ∫sin(2x) dx = ∫sin(u) (du/2) = (1/2)∫sin(u) du = (1/2)(-cos(u)) + C = -(1/2)cos(2x) + C
Nguyên hàm có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, đặc biệt là trong việc tính diện tích, thể tích, độ dài đường cong, và giải các phương trình vi phân. Việc nắm vững lý thuyết nguyên hàm là nền tảng quan trọng để học tập và nghiên cứu các môn học nâng cao hơn.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Nguyên hàm Toán 12. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập.