Chào mừng các em học sinh đến với bài giải bài tập 1.28 trang 36 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Một công ty muốn làm một đường ống dẫn từ vị trí A trên bờ biển đến vị trí B trên hòn đảo. Khoảng cách từ điểm B đến bờ biển là BH=6 km (Hình 1.42). Giá tiền để xây dựng đường ống trên bờ là 50.000 USD mỗi kilomet và giá tiền xây dựng đường ống trên biển là 130.000 USD mỗi kilomet, biết rằng AH=9 km. Xác định vị trí điểm C trên đoạn AH để khi lắp ống dẫn theo đường gấp khúc ACB thì chi phí công ty bỏ ra là thấp nhất.
Đề bài
Một công ty muốn làm một đường ống dẫn từ vị trí A trên bờ biển đến vị trí B trên hòn đảo. Khoảng cách từ điểm B đến bờ biển là BH=6 km (Hình 1.42). Giá tiền để xây dựng đường ống trên bờ là 50.000 USD mỗi kilomet và giá tiền xây dựng đường ống trên biển là 130.000 USD mỗi kilomet, biết rằng AH=9 km. Xác định vị trí điểm C trên đoạn AH để khi lắp ống dẫn theo đường gấp khúc ACB thì chi phí công ty bỏ ra là thấp nhất.

Phương pháp giải - Xem chi tiết
- Đặt HC = 𝑥 và tính đoạn CB.
- Tính tổng chi phí xây dựng đường ống trên bờ và trên biển và thiết lập hàm chi phí theo 𝑥.
- Tìm giá trị tối thiểu bằng cách khảo sát hàm chi phí theo 𝑥.
Lời giải chi tiết
- Đặt HC = 𝑥. Khi đó, AC = 9 – 𝑥. (0≤𝑥≤9)
\(CB = \sqrt {{x^2} + {6^2}} = \sqrt {{x^2} + 36} \)
- Chi phí xây dựng đường ống trên bờ: \(50.000 \times (9 - x)\)
- Chi phí xây dựng đường ống trên biển: \(130.000 \times \sqrt {{x^2} + 36} \)
- Tổng chi phí: \(50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} \)
3. Tìm giá trị tối thiểu:
- Đặt hàm chi phí: \(f(x) = 50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} \)
- Lấy đạo hàm của hàm chi phí:
\({f^\prime }(x) = - 50.000 + 130.000 \times \frac{x}{{\sqrt {{x^2} + 36} }}\)
- Giải phương trình \({f^\prime }(x) = 0\):
\(\begin{array}{l} - 50.000 + 130.000 \times \frac{x}{{\sqrt {{x^2} + 36} }} = 0\\ \Leftrightarrow 130.000 \times \frac{x}{{\sqrt {{x^2} + 36} }} = 50.000\\ \Leftrightarrow \frac{x}{{\sqrt {{x^2} + 36} }} = \frac{5}{{13}}\\ \Leftrightarrow 13x = 5\sqrt {{x^2} + 36} \\ \Leftrightarrow 169{x^2} = 25({x^2} + 36)\\ \Leftrightarrow 169{x^2} = 25{x^2} + 900\\ \Leftrightarrow 144{x^2} = 900\\ \Leftrightarrow x = \pm 2.5\end{array}\)
Loại x=−2.5 vì x ≥0
\(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} [50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} ] = 1230000\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } [50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} ] = \infty \)
- Bảng biến thiên:
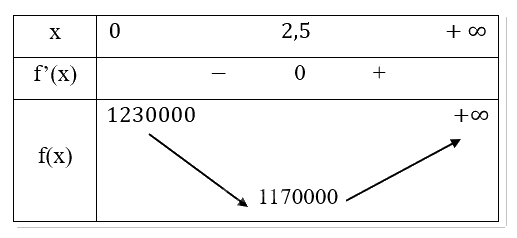
Vậy khi điểm C cách điểm H 1 khoảng là 2,5km thì chi phí công ty bỏ ra để lắp ống dẫn theo đường gấp khúc ACB là nhỏ nhất.
Bài tập 1.28 trang 36 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số. Cụ thể, bài tập thường xoay quanh việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị của hàm số, và cuối cùng là vẽ đồ thị hàm số.
Thông thường, bài tập 1.28 sẽ đưa ra một hàm số cụ thể, ví dụ như:
Học sinh cần thực hiện các bước sau để giải bài tập:
Bước 1: Tính đạo hàm cấp nhất
y' = 3x2 - 6x
Bước 2: Tìm tập xác định
Hàm số y = x3 - 3x2 + 2 có tập xác định là R (tập hợp tất cả các số thực).
Bước 3: Tìm các điểm tới hạn
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 4: Xét dấu đạo hàm
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | Đồng biến | Nghịch biến | Đồng biến |
Bước 5: Tìm cực trị
Tại x = 0, y' đổi dấu từ dương sang âm, nên hàm số đạt cực đại tại x = 0. Giá trị cực đại là y(0) = 2.
Tại x = 2, y' đổi dấu từ âm sang dương, nên hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -2.
Bước 6: Tìm giới hạn vô cùng
limx→-∞ (x3 - 3x2 + 2) = -∞
limx→+∞ (x3 - 3x2 + 2) = +∞
Bước 7: Vẽ đồ thị hàm số
Dựa trên các thông tin đã tìm được, ta có thể vẽ đồ thị hàm số y = x3 - 3x2 + 2.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài tập 1.28 trang 36 SGK Toán 12 tập 1. Chúc các em học tập tốt!