Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 24 và 25 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu!
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4\) a) Tập xác định của hàm số \(f(x)\) là gì? b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào? c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào? d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?
Trả lời câu hỏi Hoạt động 1 trang 24 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4.\)
a) Tập xác định của hàm số \(f(x)\) là gì?
b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào?
c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào?
d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?
Phương pháp giải:
a) Tập xác định: Đối với một hàm đa thức, tập xác định là toàn bộ các số thực \(R\).
b) Xét tính đơn điệu:
- Tính \({f^\prime }(x)\).
- Tìm các điểm mà tại đó \({f^\prime }(x)\) bằng 0.
- Lập bảng biến thiên.
c) Tìm cực trị: Từ bảng biến thiên, suy ra các điểm cực trị
d) Tiệm cận: Đối với hàm đa thức, không tồn tại tiệm cận ngang, đứng hay xiên.
Lời giải chi tiết:
a) Hàm số \(f(x) = - {x^3} + 3{x^2} - 4\) là một đa thức bậc ba, nên D=R.
b) Xét tính đơn điệu
Tính \({f^\prime }(x):{f^\prime }(x) = - 3{x^2} + 6x\)
Tìm nghiệm khi \({f^\prime }(x) = 0\)
\({f^\prime }(x) = 0 \leftrightarrow - 3{x^2} + 6x = 0\)
\( \leftrightarrow - 3x(x - 2) = 0\)
\( \leftrightarrow x = 0\)hoặc \(x = 2\)
Tính giới hạn
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = - \infty \\\end{array}\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
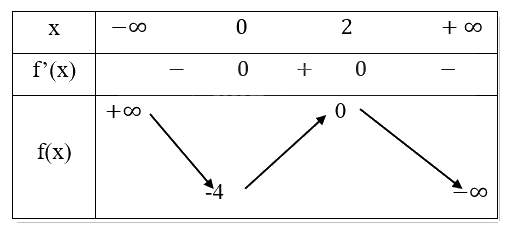
Kết luận:
- Hàm số nghịch biến trên các khoảng \(( - \infty ;0)\) và \((2; + \infty )\).
- Hàm số đồng biến trên khoảng \((0;2)\).
c) Tìm cực trị
Dựa vào bảng biến thiên, ta có thể kết luận:
- Hàm số đạt cực tiểu tại \(x = 0\)
- Hàm số đạt cực đại tại \(x = 2\)
d) Hàm số \(f(x)\) là một đa thức bậc ba, vì vậy nó không có tiệm cận ngang, đứng hay xiên. Đồ thị của hàm số không có tiệm cận.
Trả lời câu hỏi Hoạt động 1 trang 24 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4.\)
a) Tập xác định của hàm số \(f(x)\) là gì?
b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào?
c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào?
d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?
Phương pháp giải:
a) Tập xác định: Đối với một hàm đa thức, tập xác định là toàn bộ các số thực \(R\).
b) Xét tính đơn điệu:
- Tính \({f^\prime }(x)\).
- Tìm các điểm mà tại đó \({f^\prime }(x)\) bằng 0.
- Lập bảng biến thiên.
c) Tìm cực trị: Từ bảng biến thiên, suy ra các điểm cực trị
d) Tiệm cận: Đối với hàm đa thức, không tồn tại tiệm cận ngang, đứng hay xiên.
Lời giải chi tiết:
a) Hàm số \(f(x) = - {x^3} + 3{x^2} - 4\) là một đa thức bậc ba, nên D=R.
b) Xét tính đơn điệu
Tính \({f^\prime }(x):{f^\prime }(x) = - 3{x^2} + 6x\)
Tìm nghiệm khi \({f^\prime }(x) = 0\)
\({f^\prime }(x) = 0 \leftrightarrow - 3{x^2} + 6x = 0\)
\( \leftrightarrow - 3x(x - 2) = 0\)
\( \leftrightarrow x = 0\)hoặc \(x = 2\)
Tính giới hạn
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = - \infty \\\end{array}\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
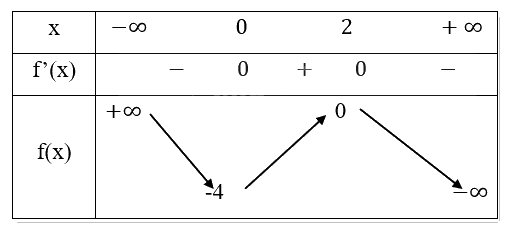
Kết luận:
- Hàm số nghịch biến trên các khoảng \(( - \infty ;0)\) và \((2; + \infty )\).
- Hàm số đồng biến trên khoảng \((0;2)\).
c) Tìm cực trị
Dựa vào bảng biến thiên, ta có thể kết luận:
- Hàm số đạt cực tiểu tại \(x = 0\)
- Hàm số đạt cực đại tại \(x = 2\)
d) Hàm số \(f(x)\) là một đa thức bậc ba, vì vậy nó không có tiệm cận ngang, đứng hay xiên. Đồ thị của hàm số không có tiệm cận.
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị hàm số, đặc biệt là các hàm số bậc hai. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Mục 1 thường bao gồm các nội dung sau:
Để xác định các hệ số a, b, c của hàm số y = x2 - 4x + 3, ta so sánh với dạng tổng quát y = ax2 + bx + c. Từ đó suy ra a = 1, b = -4, c = 3.
Tọa độ đỉnh của parabol y = ax2 + bx + c được tính theo công thức:
Trong trường hợp này, a = 2, b = 8, c = -1. Tính toán ta được xđỉnh = -2 và yđỉnh = -9. Vậy tọa độ đỉnh của parabol là (-2, -9).
Để tìm giao điểm, ta giải phương trình x2 - 2x + 1 = 3. Biến đổi phương trình ta được x2 - 2x - 2 = 0. Giải phương trình bậc hai này, ta được hai nghiệm x1 = 1 + √3 và x2 = 1 - √3. Thay các giá trị x này vào phương trình đường thẳng y = 3, ta được hai giao điểm (1 + √3, 3) và (1 - √3, 3).
Khi giải các bài tập về hàm số bậc hai, các em có thể áp dụng các phương pháp sau:
Để giải bài tập một cách chính xác và hiệu quả, các em cần lưu ý những điều sau:
Hy vọng với hướng dẫn chi tiết này, các em đã nắm vững cách giải các bài tập trong mục 1 trang 24, 25 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!