Chào mừng bạn đến với chuyên mục Lý thuyết Tích phân Toán 12 của giaitoan.edu.vn. Tại đây, chúng tôi cung cấp kiến thức nền tảng, các định nghĩa, tính chất và công thức quan trọng về tích phân một cách dễ hiểu và chi tiết.
Mục tiêu của chúng tôi là giúp bạn nắm vững lý thuyết, từ đó có thể áp dụng giải quyết các bài tập một cách hiệu quả và tự tin trong các kỳ thi quan trọng.
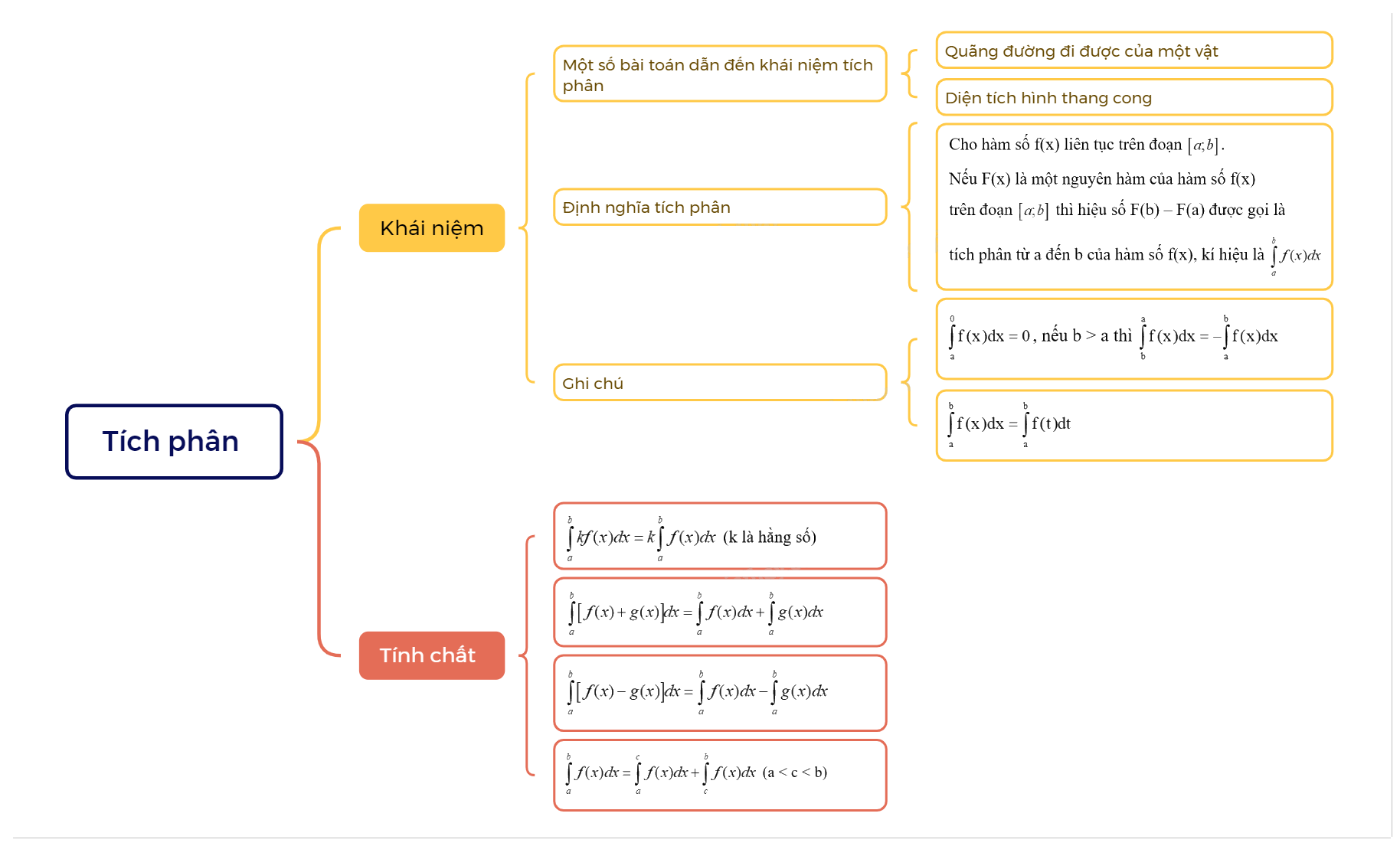
1. Khái niệm tích phân Một số bài toán dẫn đến khái niệm tích phân a) Quãng đường đi được của một vật
1. Khái niệm tích phân
Một số bài toán dẫn đến khái niệm tích phân
a) Quãng đường đi được của một vật
Xét một vật chuyển động thẳng với vận tốc v = v(t) (0 < t < T) và không đổi chiều chuyển động. Gọi F(t) là một nguyên hàm bất kỳ của v(t) trên khoảng (0;T) thì quãng đường vật đi được từ thời điểm t = a đến thời điểm t = b là L = F(b) − F(a) với 0 < a < b < T.
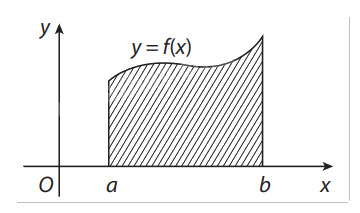
b) Diện tích hình thang cong
Cho hàm số f(x) liên tục trên đoạn [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x = a, x = bđược gọi là hình thang cong.
Trong trường hợp tổng quát, cho hàm số y = f(x) liên tục, không âm trên đoạn [a;b], người ta chứng minh được rằng diện tích hình thang cong giới hạn bởi đồ thị hàm số y=f(x), trục hoành và các đường thẳng x = a, x = b bằng F(b) − F(a), với F(x) là một nguyên hàm của f(x) trên đoạn [a;b].
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(f(x) = {x^2} + 1\) và các đường thẳng x = -1, x = 2.
Định nghĩa tích phân
| Cho hàm số f(x) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là \(\int\limits_a^b {f(x)dx} \). |
Ta còn dùng ký hiệu F(x) để chỉ hiệu số F(b) − F(a).
Vậy \(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}b\\a\end{array}} \right. = F(b) - F(a)\).
Ta gọi \(\int\limits_a^b {} \) là dấu tích phân, a là cận dưới, b là cận trên, \(f\left( x \right)dx\) là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.
Ghi chú:
- Quy ước: \(\int\limits_a^0 {f(x)dx} = 0\), nếu b > a thì \(\int\limits_b^a {f(x)dx} = - \int\limits_a^b {f(x)dx} \).
- Tích phân chỉ phụ thuộc vào hàm số dưới dấu tích phân và các cận a, b mà không phụ thuộc vào biến x hay t, nghĩa là \(\int\limits_a^b {f(x)dx} = \int\limits_a^b {f(t)dt} \).
- Ý nghĩa hình học của tích phân: Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a;b] thì diện tích S của hình thang cong (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = a, x = blà \(S = \int\limits_a^b {f(x)dx} \).
Ví dụ:
a) \(\int\limits_2^3 {3{x^2}dx} = {x^3}\left| {\begin{array}{*{20}{c}}3\\2\end{array}} \right. = {3^3} - {2^3} = 27 - 8 = 19\).
b) \(\int\limits_2^3 {{e^t}dt} = {e^t}\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right. = {e^1} - {e^0} = e - 1\).
2. Tính chất của tích phân
+ \(\int\limits_a^b {kf(x)dx = k\int\limits_a^b {f(x)dx} } \) (k là hằng số) + \(\int\limits_a^b {\left[ {f(x) + g(x)} \right]} dx = \int\limits_a^b {f(x)dx + \int\limits_a^b {g(x)dx} } \) + \(\int\limits_a^b {\left[ {f(x) - g(x)} \right]} dx = \int\limits_a^b {f(x)dx - \int\limits_a^b {g(x)dx} } \) + \(\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx + \int\limits_c^b {f(x)dx} } } \) (a < c < b) |
Ví dụ:
a) Cho \(\int\limits_0^2 {\sqrt {{e^x}} dx} = 2(e - 1)\). Tính \(\int\limits_0^2 {\frac{{\sqrt {{e^x}} }}{2}dx} \).
Ta có \(\int\limits_0^2 {\frac{{\sqrt {{e^x}} }}{2}dx} = \frac{1}{2}\int\limits_0^2 {\sqrt {{e^x}} dx} = \frac{1}{2}.2(e - 1) = e - 1\).
b) Tính \(\int\limits_0^{\frac{\pi }{2}} {(3\sin x - \cos x)dx} \).
\(\int\limits_0^{\frac{\pi }{2}} {(3\sin x - \cos x)dx} = 3\int\limits_0^{\frac{\pi }{2}} {\sin xdx} - \int\limits_0^{\frac{\pi }{2}} {\cos xdx} \)
\( = ( - 3\cos x)\left| {\begin{array}{*{20}{c}}{\frac{\pi }{2}}\\0\end{array}} \right. - \sin \left| {\begin{array}{*{20}{c}}{\frac{\pi }{2}}\\0\end{array}} \right. = - 3(0 - 1) - (1 - 0) = 2\).
c) Cho các hàm số f(x), g(x) liên tục trên đoạn [1;3] và \(\int\limits_1^2 {f(x)dx} = \frac{1}{2}\), \(\int\limits_2^3 {f(x)dx} = \frac{3}{2}\), \(\int\limits_1^3 {g(x)dx} = - 1\).
Ta có:
\(\int\limits_1^3 {f(x)dx} = \int\limits_1^2 {f(x)dx} + \int\limits_2^3 {f(x)dx} = \frac{1}{2} + \frac{3}{2} = 2\).
\(\int\limits_1^3 {[2f(x) + g(x)]dx} = 2\int\limits_1^3 {f(x)dx} + \int\limits_1^3 {f(x)dx} = 2.2 - 1 = 3\).
3. Tính tích phân trong một số trường hợp đơn giản
a) \(\int\limits_1^2 {{{(2x - 3)}^2}dx} = \int\limits_1^2 {(4{x^2} - 12x + 9)dx} = 4\int\limits_1^2 {{x^2}dx} - 12\int\limits_1^2 {xdx} + \int\limits_1^2 {9dx} \)
\( = \left( {\frac{4}{3}{x^3}} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. - \left( {6{x^2}} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. + (9x)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. = \frac{1}{3}\).
b) \(\int\limits_{ - 1}^0 {{5^{2x - 1}}dx} = \frac{1}{5}\int\limits_{ - 1}^0 {{5^{2x}}dx} = \frac{1}{5}\int\limits_{ - 1}^0 {{{25}^x}dx} = \frac{{{{25}^x}}}{{5\ln 25}}\left| {\begin{array}{*{20}{c}}0\\{ - 1}\end{array}} \right. = \frac{{24}}{{125\ln 25}}\).
c) \(\int\limits_{ - \frac{\pi }{4}}^0 {(2{{\tan }^2}x + 5)dx} = \int\limits_{ - \frac{\pi }{4}}^0 {\left[ {2(1 + {{\tan }^2}x) + 3} \right]dx} = 2\int\limits_{ - \frac{\pi }{4}}^0 {\frac{1}{{{{\cos }^2}x}}dx} + \int\limits_{ - \frac{\pi }{4}}^0 {3dx} \)
\( = 2(\tan x)\left| {\begin{array}{*{20}{c}}0\\{ - \frac{\pi }{4}}\end{array} + (3x)} \right.\left| {\begin{array}{*{20}{c}}0\\{ - \frac{\pi }{4}}\end{array}} \right. = \frac{{3\pi + 8}}{4}\).
Tích phân là một trong những khái niệm quan trọng nhất trong giải tích, đóng vai trò then chốt trong nhiều lĩnh vực khoa học và kỹ thuật. Trong chương trình Toán 12, tích phân được giới thiệu như một phép toán ngược của phép vi phân, cho phép tính diện tích dưới đường cong, thể tích của vật thể, và nhiều ứng dụng khác.
Nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Nguyên hàm không duy nhất, vì nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x), với C là một hằng số bất kỳ.
Tích phân bất định của hàm số f(x) ký hiệu là ∫f(x)dx, là tập hợp tất cả các nguyên hàm của f(x). Công thức tính tích phân bất định của một số hàm số cơ bản:
Tích phân xác định của hàm số f(x) trên đoạn [a, b] ký hiệu là ∫abf(x)dx, là một số thực biểu thị diện tích có dấu giữa đồ thị hàm số f(x), trục hoành và hai đường thẳng x = a, x = b.
Công thức tính tích phân xác định:
∫abf(x)dx = F(b) - F(a), trong đó F(x) là một nguyên hàm của f(x).
Có nhiều phương pháp tích phân khác nhau, tùy thuộc vào dạng của hàm số cần tích phân. Một số phương pháp phổ biến:
Tích phân có rất nhiều ứng dụng trong thực tế, bao gồm:
Để hiểu rõ hơn về lý thuyết tích phân, bạn nên thực hành giải nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú với các mức độ khó khác nhau, kèm theo lời giải chi tiết để bạn tham khảo.
Lý thuyết tích phân Toán 12 là một phần quan trọng của chương trình học. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn trong các kỳ thi. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất.