Chào mừng các em học sinh đến với bài giải bài tập 1.24 trang 35 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về hàm số và đồ thị.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Một chất điểm chuyển động theo quy luật \(s(t) = - {t^3} + 2t - t\), với 𝑡 (đơn vị: giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 𝑠 (đơn vị: mét) là quãng đường chất điểm di chuyển được trong khoảng thời gian đó. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 𝑠=𝑠(𝑡) trên hệ trục tọa độ 𝑡0𝑠. b) Trong khoảng thời gian 2 giây kể từ khi bắt đầu chuyển động, chất điểm đạt được vận tốc lớn nhất là bao nhiêu?
Đề bài
Một chất điểm chuyển động theo quy luật \(s(t) = - {t^3} + 2t - t\), với 𝑡 (đơn vị: giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 𝑠 (đơn vị: mét) là quãng đường chất điểm di chuyển được trong khoảng thời gian đó.
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 𝑠=𝑠(𝑡) trên hệ trục tọa độ 𝑡0𝑠.
b) Trong khoảng thời gian 2 giây kể từ khi bắt đầu chuyển động, chất điểm đạt được vận tốc lớn nhất là bao nhiêu?
Phương pháp giải - Xem chi tiết
a)
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
b)
- Xác định biểu thức vận tốc.
- Tìm các điểm t trong khoảng từ 0 đến 2 để v(t) đạt cực trị.
Lời giải chi tiết
a)
- Tập xác định: \(D = \{ x \ge 0,x \in R\} \)
- Tính đạo hàm: \(s'(t) = - 3{t^2} + 4t - 1\)
Giải phương trình: \(s'(t) = 0 \Leftrightarrow - 3{t^2} + 4t - 1 = 0 \Rightarrow {t_1} = 1,{t_2} = \frac{1}{3}\)
- Giới hạn
\(\mathop {\lim }\limits_{t \to \infty } s(t) = \mathop {\lim }\limits_{t \to \infty } \left( { - {t^3} + 2{t^2} - t} \right) = - \infty \)
- Bảng biến thiên:
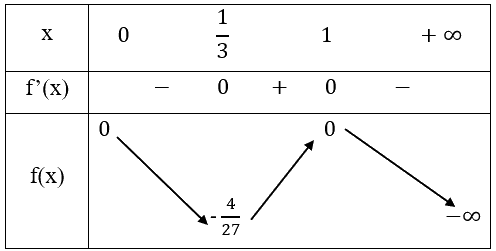
- Vẽ đồ thị
Hàm số nghịch biến trên khoảng (0, \(\frac{1}{3}\)) và (1,∞)
Hàm số đồng biến trên khoảng (\(\frac{1}{3}\),1)
Cực trị: Hàm số đạt cực tiểu tại \(x = \frac{1}{2},{y_{CT}} = - \frac{4}{{27}}\)
Hàm số đạt cực đại tại \(x = 1,{y_{CD}} = 0\)
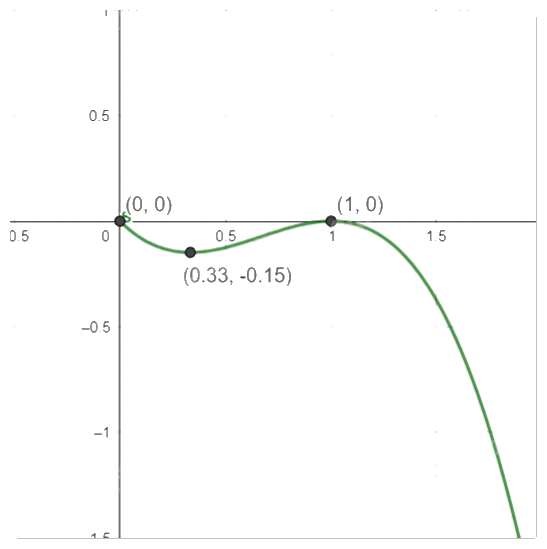
b)
Ta có vận tốc: \(v(t) = s'(t) = - 3{t^2} + 4t - 1\)
Điểm cực trị của vận tốc:
Giải \(s''(t) = 0\): \( - 6t + 4 = 0 \Rightarrow t = \frac{2}{3}\)
Vận tốc tại các điểm biên và cực trị:
\(\begin{array}{l}v(0) = - {3.0^2} + 4.0 - 1 = - 1\\v\left( {\frac{2}{3}} \right) = - 3{\left( {\frac{2}{3}} \right)^2} + 4\left( {\frac{2}{3}} \right) - 1 = - \frac{{12}}{9} + \frac{8}{3} - 1 = - \frac{4}{3} + \frac{8}{3} - 1 = \frac{1}{3}\\v(2) = - 3 \cdot {2^2} + 4 \cdot 2 - 1 = - 12 + 8 - 1 = - 5\end{array}\)
Vậy, vận tốc lớn nhất trong khoảng thời gian 2 giây là \(\frac{1}{3}\) m/s.
Bài tập 1.24 trang 35 SGK Toán 12 tập 1 thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm cực trị, hoặc vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Bước đầu tiên là xác định tập xác định của hàm số. Tập xác định là tập hợp tất cả các giá trị của x mà tại đó hàm số có nghĩa. Việc xác định tập xác định giúp chúng ta giới hạn phạm vi khảo sát của hàm số.
Sau khi xác định tập xác định, chúng ta cần tính đạo hàm cấp nhất của hàm số. Đạo hàm cấp nhất cho phép chúng ta xác định được khoảng đồng biến, nghịch biến của hàm số.
Điểm dừng là các điểm mà tại đó đạo hàm cấp nhất bằng 0 hoặc không tồn tại. Việc xét dấu đạo hàm cấp nhất trên các khoảng xác định giúp chúng ta xác định được khoảng đồng biến, nghịch biến của hàm số.
Cực trị của hàm số là các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trong một khoảng nào đó. Chúng ta có thể tìm cực trị bằng cách xét dấu đạo hàm cấp nhất hoặc sử dụng đạo hàm cấp hai.
Sau khi xác định được các yếu tố cơ bản như tập xác định, khoảng đồng biến, nghịch biến, cực trị, chúng ta có thể vẽ đồ thị hàm số. Đồ thị hàm số giúp chúng ta hình dung được hình dạng của hàm số và các tính chất của nó.
Giả sử bài tập 1.24 yêu cầu chúng ta khảo sát hàm số y = x3 - 3x2 + 2. Chúng ta sẽ tiến hành giải bài tập theo các bước sau:
Bài tập 1.24 trang 35 SGK Toán 12 tập 1 là một bài tập quan trọng giúp chúng ta củng cố kiến thức về hàm số và đồ thị. Bằng cách áp dụng các phương pháp giải bài tập một cách linh hoạt và sáng tạo, chúng ta có thể giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt nhất.