Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1

Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 - Cùng khám phá

Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1

Chào mừng các em học sinh đến với bài giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.

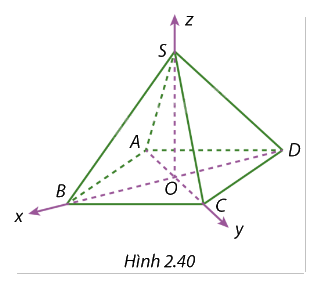
Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết SA = a. SO = h. Xét hệ toạ độ Oxyz với các tia Ox, Oy, Oz tương ứng trùng với các tia OB, OC, OS như ở Hình 2.40. Hãy xác định toạ độ các điểm S, A, B, C, D.

Đề bài

Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 - Cùng khám phá 2

- Tính khoảng cách từ các đỉnh ABCD đến O.

- Sử dụng tính chất của hình vuông, xác định tọa độ các đỉnh A, B, C, D.

- Dựa vào chiều cao h của hình chóp (tức là độ dài đoạn SO) và độ dài SA = a, sử dụng hệ tọa độ Oxyz để xác định tọa độ của điểm S.

Lời giải chi tiết

Tam giác SOA vuông tại O nên: \(OA = \sqrt {S{A^2} - S{O^2}} = \sqrt {{a^2} - {h^2}} \)

Vì ABCD là hình vuông nên: \(OA = OB = OC = OD = \sqrt {{a^2} - {h^2}} \)

Toạ độ của các đỉnh A, B, C, D là: \(A = \left( {0, - \sqrt {{a^2} - {h^2}} ,0} \right);B = \left( {\sqrt {{a^2} - {h^2}} ,0,0} \right);C = \left( {0,\sqrt {{a^2} - {h^2}} ,0} \right);D = \left( { - \sqrt {{a^2} - {h^2}} ,0,0} \right)\)

Điểm S có tọa độ \(S({x_S},{y_S},{z_S})\) với z_S = h và SA = a. Do điểm S nằm trên trục Oz, tọa độ của S trong hệ tọa độ Oxyz là (0, 0, h).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 - Cùng khám phá đặc sắc thuộc chuyên mục đề toán lớp 12 trên nền tảng soạn toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1: Phân tích chi tiết và phương pháp giải

Bài tập 2.15 trang 73 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm và ứng dụng của đạo hàm. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:

Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của một hàm số tại một điểm.
Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản (hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit) và các quy tắc tính đạo hàm của hàm hợp, hàm ẩn.
Ứng dụng của đạo hàm: Biết cách sử dụng đạo hàm để khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn) và giải các bài toán liên quan đến tối ưu hóa.

Nội dung bài tập 2.15 trang 73 SGK Toán 12 tập 1

Bài tập 2.15 thường yêu cầu học sinh:

Tính đạo hàm của một hàm số cho trước.
Khảo sát hàm số bằng cách sử dụng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn).
Giải các bài toán tối ưu hóa (tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).

Phương pháp giải bài tập 2.15 trang 73 SGK Toán 12 tập 1

Để giải bài tập 2.15 trang 73 SGK Toán 12 tập 1, chúng ta có thể áp dụng các bước sau:

Bước 1: Tính đạo hàm: Tính đạo hàm cấp một (y') của hàm số.
Bước 2: Tìm điểm dừng: Giải phương trình y' = 0 để tìm các điểm dừng của hàm số.
Bước 3: Khảo sát dấu của đạo hàm: Lập bảng biến thiên của đạo hàm y' để xác định khoảng đồng biến, nghịch biến của hàm số.
Bước 4: Xác định cực trị: Sử dụng bảng biến thiên hoặc các tiêu chuẩn xét cực trị để xác định các điểm cực đại, cực tiểu của hàm số.
Bước 5: Tính đạo hàm cấp hai: Tính đạo hàm cấp hai (y'') của hàm số.
Bước 6: Tìm điểm uốn: Giải phương trình y'' = 0 để tìm các điểm uốn của hàm số.
Bước 7: Khảo sát dấu của đạo hàm cấp hai: Lập bảng biến thiên của đạo hàm cấp hai y'' để xác định khoảng lồi, lõm của hàm số.
Bước 8: Vẽ đồ thị hàm số: Dựa vào các kết quả đã tìm được, vẽ đồ thị hàm số.

Ví dụ minh họa giải bài tập 2.15 trang 73 SGK Toán 12 tập 1

Giả sử bài tập 2.15 yêu cầu khảo sát hàm số y = x³ - 3x² + 2.

Giải:

Tính đạo hàm: y' = 3x² - 6x
Tìm điểm dừng: 3x² - 6x = 0 => x = 0 hoặc x = 2
Khảo sát dấu của đạo hàm:
x -∞ 0 2 +∞
y' + - +
y ↗ ↘ ↗
Xác định cực trị: Hàm số đạt cực đại tại x = 0, y_max = 2. Hàm số đạt cực tiểu tại x = 2, y_min = -2.
Tính đạo hàm cấp hai: y'' = 6x - 6
Tìm điểm uốn: 6x - 6 = 0 => x = 1
Khảo sát dấu của đạo hàm cấp hai:
x -∞ 1 +∞
y'' - +
y ∩ ∪
Vẽ đồ thị hàm số: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số y = x³ - 3x² + 2.

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

x	-∞	1	+∞
y''	-	+
y	∩	∪

Lưu ý khi giải bài tập 2.15 trang 73 SGK Toán 12 tập 1

Luôn kiểm tra lại các bước tính toán để tránh sai sót.
Sử dụng máy tính cầm tay để hỗ trợ tính toán.
Nắm vững các định lý và công thức liên quan đến đạo hàm và ứng dụng của đạo hàm.
Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.

Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 một cách hiệu quả. Chúc các em học tập tốt!