Phương trình mặt phẳng là một trong những kiến thức quan trọng của chương trình Hình học không gian Toán 12. Việc nắm vững lý thuyết và phương pháp giải bài tập liên quan đến phương trình mặt phẳng sẽ giúp các em học sinh đạt kết quả tốt trong các kỳ thi quan trọng.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập đa dạng, giúp các em học sinh hiểu sâu sắc về lý thuyết và rèn luyện kỹ năng giải bài tập một cách hiệu quả.
1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng Vecto pháp tuyến
1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng
Vecto pháp tuyến
| Vecto \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vecto pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\). |
Cặp vecto chỉ phương
| Cho mặt phẳng \(\left( \alpha \right)\). Nếu hai vecto \(\overrightarrow a ,\overrightarrow b \) không cùng phương, có giá song song hoặc nằm trong \(\left( \alpha \right)\) thì \(\overrightarrow a ,\overrightarrow b \) được gọi là cặp vecto chỉ phương của \(\left( \alpha \right)\). |
Ví dụ: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Hãy tìm bốn vecto pháp tuyến và hai cặp vecto chỉ phương của mặt phẳng (AA’B’B).
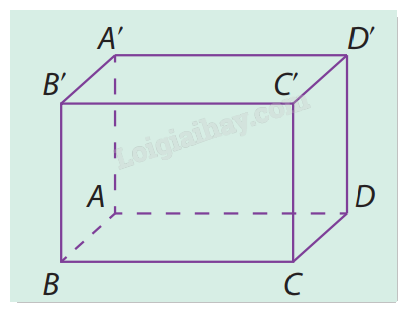
Giải:
Bốn vecto pháp tuyến của mặt phẳng (AA’B’B) là: \(\overrightarrow {AD} \), \(\overrightarrow {A'D'} \), \(\overrightarrow {BC} \), \(\overrightarrow {B'C'} \).
Hai cặp vecto chỉ phương của mặt phẳng (AA’B’B) là: \(\overrightarrow {AB} \), \(\overrightarrow {AA'} \) và \(\overrightarrow {AB} \), \(\overrightarrow {AB'} \).
Xác định vecto pháp tuyến của mặt phẳng khi biết cặp vecto chỉ phương
Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) nhận hai vecto \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\) làm cặp vecto chỉ phương thì \(\left( \alpha \right)\) nhận vecto \(\overrightarrow n = ({a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1})\) làm vecto pháp tuyến. |
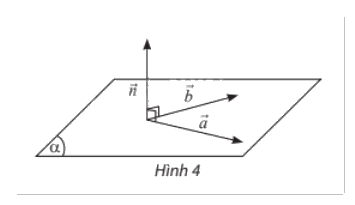
Vecto \(\overrightarrow n = ({a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1})\) còn được gọi là tích có hướng của hai vecto \(\overrightarrow a = ({a_1};{a_2};{a_3})\) và \(\overrightarrow b = ({b_1};{b_2};{b_3})\), kí hiệu là \(\left[ {\overrightarrow a ,\overrightarrow b } \right]\).
Biểu thức \({a_1}{b_2} - {a_2}{b_1}\) thường được kí hiệu là \(\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|\).
Nếu \(\overrightarrow a ,\overrightarrow b \) cùng phương \( \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right] = 0\).
Ví dụ: Cho mặt phẳng (P) nhận \(\overrightarrow a = (1;2;3)\), \(\overrightarrow b = (4;1;5)\) làm cặp vecto chỉ phương. Tìm một vecto pháp tuyến của (P).
Giải: Ta có tích có hướng của hai vecto \(\overrightarrow a \), \(\overrightarrow b \) là
\(\left[ {\overrightarrow a ,\overrightarrow b } \right] = (2.5 - 3.1;3.4 - 1.5;1.1 - 2.4) = (7;7; - 7)\).
Do đó, mặt phẳng (P) nhận \(\overrightarrow n = \frac{1}{7}\left[ {\overrightarrow a ,\overrightarrow b } \right] = (1;1; - 1)\) làm một vecto pháp tuyến.
2. Phương trình tổng quát của mặt phẳng
Định nghĩa
| Trong không gian Oxyz, mỗi mặt phẳng đều có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng đó. |
Mỗi phương trình Ax + By + Cz + D = 0 (A, B, C không đồng thời bằng 0) đều xác định một mặt phẳng nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến.
Cho mặt phẳng có phương trình tổng quát là Ax + By + Cz + D = 0 . Khi đó \(N({x_0};{y_0};{z_0}) \in (\alpha ) \Leftrightarrow A{x_0} + B{y_0} + C{z_0} + D = 0\).
Ví dụ: Cho hai mặt phẳng (P), (Q) có phương trình tổng quát là
(P): \(3x - 5y + 7z = 0\) và (Q): \(x + y - 2 = 0\).
a) Tìm một vecto pháp tuyến của mỗi mặt phẳng (P), (Q).
b) Tìm điểm thuộc mặt phẳng (P) trong số các điểm A(1;3;1), B(1;2;3).
Giải:
a) Mặt phẳng (P) có một vecto pháp tuyến là \(\overrightarrow n = (3; - 5;7)\).
Mặt phẳng (Q) có một vecto pháp tuyến là \(\overrightarrow n = (1;1;0)\).
b) Thay tọa độ điểm A vào phương trình của (P), ta được: 3.1 – 5.3 + 7.1 + 5 = 0.
Vậy A thuộc (P).
Thay tọa độ điểm B vào phương trình của (P), ta được: 3.1 – 5.2 + 7.3 + 5 = 19 \( \ne 0\).
Vậy B không thuộc (P).
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết vecto pháp tuyến
Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\) có phương trình là: \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0 \Leftrightarrow Ax + By + Cz + D = 0\), với \(D = - (A{x_0} + B{y_0} + C{z_0})\). |
Ví dụ: Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và có vecto pháp tuyến \(\overrightarrow n = (1;2;1)\).
Giải: Vì (P) đi qua điểm M(1;2;1) và có vecto pháp tuyến \(\overrightarrow n = (1;2;1)\) nên phương trình của (P) là \(1\left( {x-1} \right) + 2\left( {y-2} \right) + 1\left( {z-3} \right) = 0 \Leftrightarrow x + 2y - 8 = 0\).
Lập phương trình mặt phẳng đi qua một điểm và biết cặp vecto chỉ phương
Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương \(\overrightarrow u \), \(\overrightarrow v \) có thể thực hiện theo các bước sau: - Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). - Lập phương trình tổng quát của mặt phẳng đi qua M và biết vecto pháp tuyến \(\overrightarrow n \). |
Ví dụ: Viết phương trình mặt phẳng (P) đi qua điểm N(4;0;1) và có cặp vecto chỉ phương là \(\overrightarrow a = (1;2;1)\), \(\overrightarrow b = (2;1;3)\).
Giải: (P) có cặp vecto chỉ phương là \(\overrightarrow a = (1;2;1)\), \(\overrightarrow b = (2;1;3)\), suy ra (P) có vecto pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow a ,\overrightarrow b } \right] = (2.3 - 1.1;1.2 - 1.3;1.1 - 2.2) = (5; - 1; - 3)\).
Phương trình của (P) là \(5(x - 4) - 1(y - 0) - 3(z - 1) = 0 \Leftrightarrow 5x - y - 3z - 17 = 0\).
Lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng
Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau: - Tìm cặp vecto chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \). - Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\). - Lập phương trình tổng quát của mặt phẳng đi qua A (hoặc B, C) và biết vecto pháp tuyến \(\overrightarrow n \). |
Ví dụ: Viết phương trình mặt phẳng (P) đi qua ba điểm A(1;1;1), B(1;2;2), C(4;1;0).
Giải: (P) đi qua ba điểm A(1;1;1), B(1;2;2), C(4;1;0) nên có cặp vecto chỉ phương là \(\overrightarrow {AB} = (0;1;1)\), \(\overrightarrow {AC} = (3;0; - 1)\), suy ra (P) có vecto pháp tuyến là
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (1.( - 1) - 1.0;1.3 - 0.( - 1);0.0 - 1.3) = ( - 1;3; - 3)\).
Phương trình của (P) là \( - 1(x - 1) + 3(y - 1) - 3(z - 1) = 0 \Leftrightarrow x - 3y + 3z = 0\).
Phương trình mặt phẳng theo đoạn chắn
| Phương trình mặt phẳng cắt ba trục tọa độ tại ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c \( \ne \) 0 có dạng \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) gọi là phương trình mặt phẳng theo đoạn chắn. |
3. Điều kiện để hai mặt phẳng song song, vuông góc
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( {{\alpha _1}} \right):{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\), \(\left( {{\alpha _2}} \right):{A_2}x + {B_2}y + {C_2}z + {D_2} = 0\) với hai vecto pháp tuyến \(\overrightarrow {{n_1}} = ({A_1};{B_1};{C_1})\), \(\overrightarrow {{n_2}} = ({A_2};{B_2};{C_2})\) tương ứng. Giả sử điểm \(M \in ({\alpha _1})\).
Điều kiện để hai mặt phẳng song song
Hai mặt phẳng \(\left( {{\alpha _1}} \right)\) và \(\left( {{\alpha _2}} \right)\) song song khi và chỉ khi \(\overrightarrow {{n_1}} \) cùng phương với \(\overrightarrow {{n_2}} \) và \(M \notin ({\alpha _2})\). Trong trường hợp \({A_2}.{B_2}.{C_2}.{D_2} \ne 0\) thì: \(\left( {{\alpha _1}} \right)//\left( {{\alpha _2}} \right) \Leftrightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} \ne \frac{{{D_1}}}{{{D_2}}}\) |
Điều kiện để hai mặt phẳng trùng nhau
Hai mặt phẳng \(\left( {{\alpha _1}} \right)\) và \(\left( {{\alpha _2}} \right)\) trùng nhau khi và chỉ khi \(\overrightarrow {{n_1}} \) cùng phương với \(\overrightarrow {{n_2}} \) và \(M \in ({\alpha _2})\). Trong trường hợp \({A_2}.{B_2}.{C_2}.{D_2} \ne 0\) thì: \(\left( {{\alpha _1}} \right) \equiv \left( {{\alpha _2}} \right) \Leftrightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} = \frac{{{D_1}}}{{{D_2}}}\) |
Ví dụ: Trong không gian Oxyz, cho mặt phẳng (P): \(2x - 3y + z + 5 = 0\).
a) Chứng minh rằng mặt phẳng (Q): \( - 4x + 6y - 2z + 7 = 0\) song song với (P).
b) Viết phương trình mặt phẳng (P’) đi qua điểm M(1;-2;3) và song song với (P).
Giải:
a) Xét (P): \(2x - 3y + z + 5 = 0\) và (Q): \( - 4x + 6y - 2z + 7 = 0\).
Ta có \(\frac{2}{{ - 4}} = \frac{{ - 3}}{6} = \frac{1}{{ - 2}} \ne \frac{5}{7}\) nên (P)//(Q).
b) Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (2; - 3;1)\).
Vì (P’)//(P) nên (P’) có vecto pháp tuyến \(\overrightarrow n = (2; - 3;1)\).
Vậy mặt phẳng (P’) đi qua đi qua M(1;-2;3) và có vecto pháp tuyến \(\overrightarrow n = (2; - 3;1)\) có phương trình là: \(2(x - 1) - 3(y + 2) + 1(z - 3) = 0\) hay \(2x - 3y + z - 11 = 0\).
Điều kiện để hai mặt phẳng cắt nhau
Hai mặt phẳng \(\left( {{\alpha _1}} \right)\) và \(\left( {{\alpha _2}} \right)\) cắt nhau khi và chỉ khi \(\overrightarrow {{n_1}} \) không cùng phương với \(\overrightarrow {{n_2}} \). Trong trường hợp \({A_2}.{B_2}.{C_2} \ne 0\) thì: \(\left( {{\alpha _1}} \right) \cap \left( {{\alpha _2}} \right) \Leftrightarrow \frac{{{A_1}}}{{{A_2}}} \ne \frac{{{B_1}}}{{{B_2}}}\) hoặc \(\frac{{{A_1}}}{{{A_2}}} \ne \frac{{{C_1}}}{{{C_2}}}\) hoặc \(\frac{{{B_1}}}{{{B_2}}} \ne \frac{{{C_1}}}{{{C_2}}}\) |
Điều kiện để hai mặt phẳng vuông góc
Xét hai mặt phẳng \(\left( {{\alpha _1}} \right)\) và \(\left( {{\alpha _2}} \right)\). \(\left( {{\alpha _1}} \right) \bot \left( {{\alpha _2}} \right) \Leftrightarrow \overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \Leftrightarrow {A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2} = 0\) |
Ví dụ: Cho ba mặt phẳng (P), (Q), (R) có phương trình là
(P): \(x - 4y + 3z + 2 = 0\), (Q): \(4x + y + 88 = 0\), (R): \(x + y + z + 9 = 0\). Chứng minh rằng (P) ⊥ (Q), (P) ⊥ (R).
Giải: Các mặt phẳng (P), (Q), (R) có vecto pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = (1; - 4;3)\), \(\overrightarrow {{n_2}} = (4;1;0)\), \(\overrightarrow {{n_3}} = (1;1;1)\).
Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.4 + ( - 4).1 + 3.0 = 0\). Vậy (P) ⊥ (Q).
Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_3}} = 1.1 + ( - 4).1 + 3.1 = 0\). Vậy (P) ⊥ (R).
4. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian Oxyz, khoảng cách từ điểm \(M({x_0};{y_0};{z_0})\) đến mặt phẳng \((\alpha )\): Ax + By + Cz + D = 0 là: \(d(M,(P)) = \frac{{\left| {A{x_0}{\rm{ }} + {\rm{ }}B{y_0}{\rm{ }} + {\rm{ }}C{z_0}{\rm{ }} + {\rm{ }}D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\) |
Ví dụ 1: Tìm khoảng cách từ điểm M(1;2;3) đến mặt phẳng (P): \(x + y + z + 12 = 0\).
Giải: \(d\left( {M,(P)} \right) = \frac{{\left| {1.1 + 1.2 + 1.3 + 12} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{18}}{{\sqrt 3 }} = 6\sqrt 3 \).
Ví dụ 2: Chứng minh \((\alpha )\): 2x + 3y – 6z – 7 = 0 song song với \((\beta )\): 2x + 3y – 6z + 14 = 0 và tìm khoảng cách giữa chúng.
Giải:
Ta có \(\frac{2}{2} = \frac{3}{3} = \frac{{ - 6}}{{ - 6}} \ne \frac{{ - 7}}{{14}}\) nên \((\alpha )\)//\((\beta )\). Lấy điểm N(-7;0;0) thuộc \((\beta )\).
Vậy \(d\left( {(\alpha ),(\beta )} \right) = d\left( {N,(\alpha )} \right) = \frac{{\left| {2.( - 7) + 3.0 - 6.3 - 7} \right|}}{{\sqrt {{2^2} + {3^2} + {{( - 6)}^2}} }} = \frac{{21}}{7} = 3\).
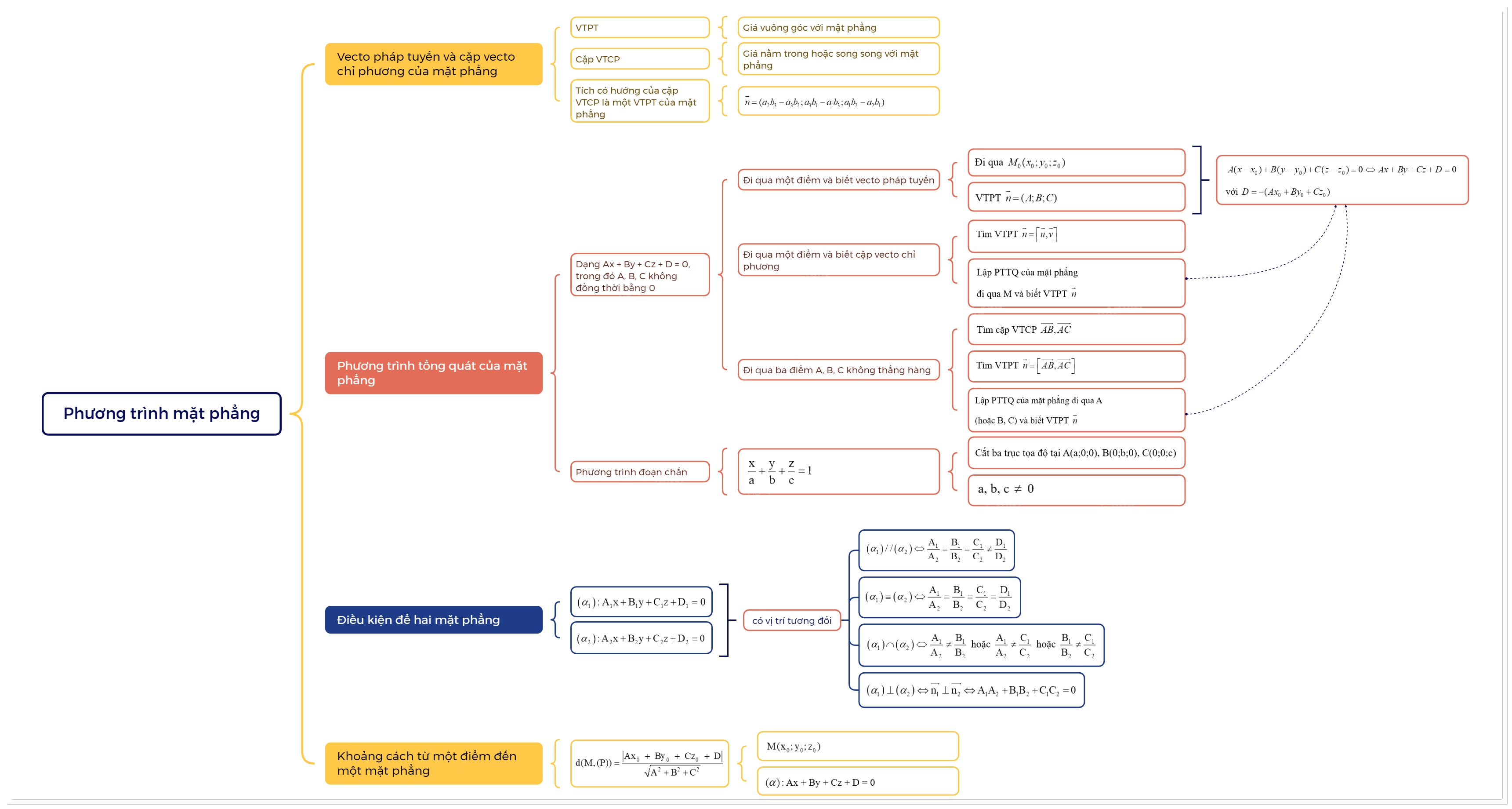
Trong không gian Oxyz, một mặt phẳng được xác định duy nhất bởi một điểm thuộc mặt phẳng và một vector pháp tuyến của mặt phẳng. Phương trình mặt phẳng là một phương trình đại số biểu diễn tập hợp tất cả các điểm thuộc mặt phẳng đó.
Một vector n được gọi là vector pháp tuyến của mặt phẳng (P) nếu n vuông góc với mọi vector nằm trong mặt phẳng (P).
Phương trình tổng quát của mặt phẳng (P) có dạng: Ax + By + Cz + D = 0, trong đó (A, B, C) là vector pháp tuyến của mặt phẳng.
Nếu mặt phẳng (P) đi qua điểm M0(x0, y0, z0) và có vector pháp tuyến n = (A, B, C) thì phương trình của (P) là:
A(x - x0) + B(y - y0) + C(z - z0) = 0
Nếu mặt phẳng (P) đi qua ba điểm A(xA, yA, zA), B(xB, yB, zB), C(xC, yC, zC) không thẳng hàng thì phương trình của (P) có thể được tìm bằng cách sử dụng định thức:
| x - xA y - yA z - zA |
| xB - xA yB - yA zB - zA | = 0
| xC - xA yC - yA zC - zA |
Phương trình có dạng: By + Cz + D = 0
Phương trình có dạng: Ax + Cz + D = 0
Phương trình có dạng: Ax + By + D = 0
Cho điểm M(xM, yM, zM) và mặt phẳng (P): Ax + By + Cz + D = 0.
Cho hai mặt phẳng (P1): A1x + B1y + C1z + D1 = 0 và (P2): A2x + B2y + C2z + D2 = 0.
Chúng tôi sẽ cung cấp các bài tập ví dụ minh họa cụ thể để giúp các em hiểu rõ hơn về cách áp dụng lý thuyết vào giải bài tập.
Hy vọng với những kiến thức trên, các em sẽ nắm vững lý thuyết Phương trình mặt phẳng Toán 12 và tự tin giải các bài tập liên quan.