Chào mừng các em học sinh đến với bài giải bài tập 1.15 trang 21 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán về hàm số và đồ thị.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
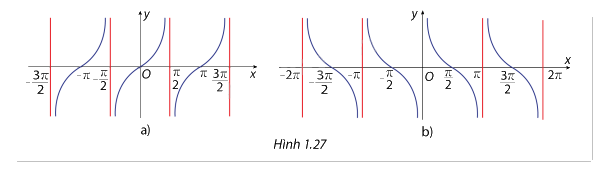
Xác định các đường tiệm cận đứng của các đồ thị hàm số \(y = \tan x\) ( hình 1.27a) và \(y = \cot x\) (hình 1.27b).
Đề bài
Xác định các đường tiệm cận đứng của các đồ thị hàm số \(y = \tan x\) ( hình 1.27a) và \(y = \cot x\) (hình 1.27b).
Lời giải chi tiết
Đường tiệm cận đứng của hàm số \(\tan x\) là \(\frac{x}{2} + k\pi \) \((k \in \mathbb{Z})\).
Đường tiệm cận đứng của hàm số \(\tan x\) là \(k\pi \) \((k \in \mathbb{Z})\).
Bài tập 1.15 trang 21 SGK Toán 12 tập 1 thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm cực trị, hoặc vẽ đồ thị hàm số. Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Bước đầu tiên là xác định tập xác định của hàm số. Điều này giúp chúng ta biết được những giá trị nào của x mà hàm số có nghĩa. Ví dụ, nếu hàm số chứa mẫu số, chúng ta cần đảm bảo mẫu số khác 0.
Sau khi xác định tập xác định, chúng ta cần tính đạo hàm cấp một của hàm số. Đạo hàm cấp một cho chúng ta biết được tốc độ thay đổi của hàm số tại mỗi điểm.
Các điểm dừng của hàm số là những điểm mà đạo hàm cấp một bằng 0 hoặc không tồn tại. Đây là những điểm tiềm năng có thể là cực trị của hàm số.
Chúng ta cần khảo sát dấu của đạo hàm cấp một trên các khoảng xác định của hàm số. Dựa vào dấu của đạo hàm cấp một, chúng ta có thể xác định được khoảng hàm số đồng biến, nghịch biến.
Dựa vào dấu của đạo hàm cấp một khi đi qua các điểm dừng, chúng ta có thể xác định được cực đại, cực tiểu của hàm số.
Trong một số trường hợp, chúng ta cần tính đạo hàm cấp hai để xác định tính lồi, lõm của hàm số và tìm điểm uốn.
Cuối cùng, chúng ta sử dụng các thông tin đã thu thập được để vẽ đồ thị hàm số. Đồ thị hàm số giúp chúng ta hình dung được hình dạng của hàm số và các đặc điểm quan trọng của nó.
Giả sử bài tập yêu cầu khảo sát hàm số y = x3 - 3x2 + 2. Chúng ta sẽ thực hiện các bước sau:
Dựa vào các thông tin trên, chúng ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Giải bài tập 1.15 trang 21 SGK Toán 12 tập 1 đòi hỏi chúng ta phải nắm vững các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bằng cách thực hiện các bước một cách cẩn thận và chính xác, chúng ta có thể giải quyết bài tập này một cách hiệu quả. Chúc các em học tập tốt!