Chào mừng các em học sinh đến với bài giải chi tiết bài tập 1.48 trang 49 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến kiến thức đã học.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin hơn trong quá trình học tập.
Đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\) là đường cong trong hình nào dưới đây?
Đề bài
Đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\) là đường cong trong hình nào dưới đây?
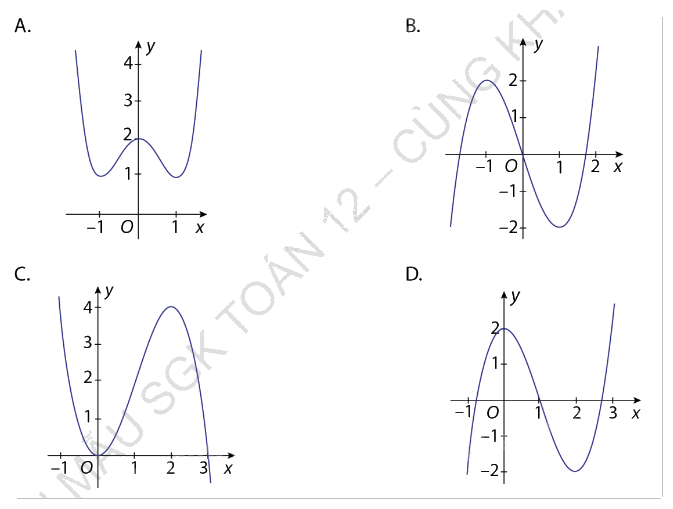
Phương pháp giải - Xem chi tiết
Đồ thị hàm số bậc 3 \(a{x^3} + b{x^2} + cx + d\) thường có những đặc điểm như sau:
- Có 2 cực trị hoặc không có cực trị nào.
- Luôn nhận điểm uốn làm tâm đối xứng.
- Khi ac < 0 thì 2 điểm cực trị sẽ nằm 2 phía so với trục Oy.
- Nếu hệ số a > 0, đồ thị đi từ phía dưới bên trái (hướng xuống) lên phía trên bên phải (hướng lên).
- Nếu hệ số a < 0, đồ thị đi từ phía trên bên trái (hướng lên) xuống phía dưới bên phải (hướng xuống).
- Đồ thị luôn cắt trục tung tại một điểm (khi x = 0, giá trị này là d).
Lời giải chi tiết
Loại A vì có đến 3 cực trị.
Theo đề bài ta có a = 1 > 0 nên đồ thị sẽ đi từ phía dưới bên trái, suy ra loại C.
Theo đề bài ta có d = 2 nên đồ thị sẽ cắt trục tung tại điểm (0;2), suy ra loại B.
Đáp án đúng là D.
Bài tập 1.48 trang 49 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này một cách hiệu quả, chúng ta cần phân tích kỹ đề bài, xác định các yếu tố quan trọng và áp dụng các công thức, định lý phù hợp.
Đề bài: (Đề bài cụ thể của bài tập 1.48 sẽ được chèn vào đây)
Phân tích: Để giải quyết bài toán này, chúng ta cần:
Bước 1: (Giải thích chi tiết bước 1, kèm theo các phép tính và giải thích rõ ràng)
Bước 2: (Giải thích chi tiết bước 2, kèm theo các phép tính và giải thích rõ ràng)
Bước 3: (Giải thích chi tiết bước 3, kèm theo các phép tính và giải thích rõ ràng)
...
Để hiểu rõ hơn về phương pháp giải bài tập này, chúng ta cùng xem xét một ví dụ minh họa:
Ví dụ: (Ví dụ minh họa cụ thể)
Lời giải: (Lời giải chi tiết cho ví dụ)
Ngoài ra, các em có thể tham khảo thêm một số bài tập tương tự để rèn luyện kỹ năng:
Khi giải các bài toán về đường thẳng và mặt phẳng trong không gian, các em cần lưu ý:
Bài tập 1.48 trang 49 SGK Toán 12 tập 1 là một bài toán điển hình về ứng dụng của kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa, các em đã nắm vững phương pháp giải và tự tin hơn trong quá trình học tập. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| Khoảng cách từ điểm M đến mặt phẳng (P) | d(M, (P)) = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2) |
| Góc giữa đường thẳng d và mặt phẳng (P) | sin φ = |aA + bB + cC| / √(a2 + b2 + c2)√(A2 + B2 + C2) |