Chào mừng các em học sinh đến với bài giải chi tiết bài tập 1.35 trang 46 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: a) \(y = \frac{{3x + 6}}{{2 - x}}\) b) \(y = 2x + \frac{3}{{2 - x}}\)
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = \frac{{3x + 6}}{{2 - x}}\)
b) \(y = 2x + \frac{3}{{2 - x}}\)
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
Lời giải chi tiết
a)
- Tập xác định: \(D = R\backslash \{ 2\} \)
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x + 6}}{{2 - x}} = - 3\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 6}}{{2 - x}} = - 3\)
Suy ra đường thẳng \({\rm{y}} = - 3\) là đường tiệm cận ngang của đồ thị hàm số đã cho
\(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{3x + 6}}{{2 - x}} = - \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{3x + 6}}{{2 - x}} = \infty \)
Suy ra đường thẳng \({\rm{x}} = 2\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Ta có: \({y^\prime } = \frac{{12}}{{{{(2 - x)}^2}}} > 0\forall x \in D\)
Suy ra hàm số đồng biến trên tập xác định
Bảng biến thiên:
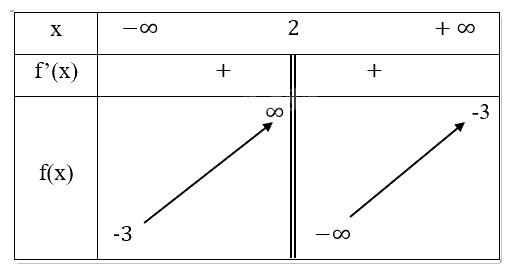
Cực trị: Hàm số không có cực trị
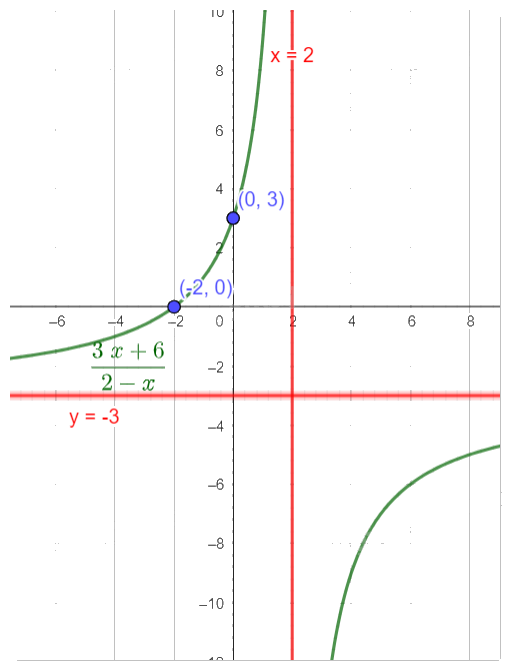
- Vẽ đồ thị
Tiệm cận đứng: \(x = 2\) và tiệm cận ngang \(y = - 3\)
Giao với trục Oy tại điểm (0,3)
Giao với trục Ox tại điểm (-2,0)
b)
- Tập xác định: \(D = R\backslash \{ 2\} \)
- Sự biến thiên:
Giới hạn, tiệm cận:
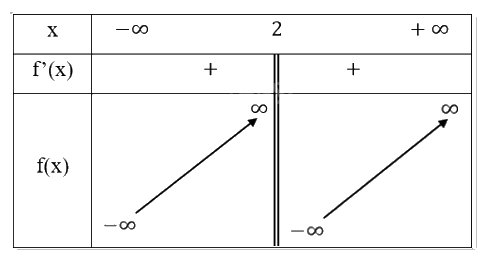
\[\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + \frac{3}{{2 - x}}} \right) = \infty \]
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + \frac{3}{{2 - x}}} \right) = - \infty \)
Suy ra hàm số không có tiệm cận ngang
\(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {2x + \frac{3}{{2 - x}}} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + \frac{3}{{2 - x}}} \right) = \infty \)
Suy ra đường thẳng \({\rm{x}} = 2\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Khi \(x \to \pm \infty ,\frac{3}{{2 - x}} \to 0\)nên đường thẳng \(y = 2x\) là tiệm cận xiên của đồ thị hàm số đã cho.
Ta có: \({y^\prime } = 2 + \frac{3}{{{{(2 - x)}^2}}} > 0\forall x \in D\)
Suy ra hàm số đồng biến trên tập xác định
Bảng biến thiên:
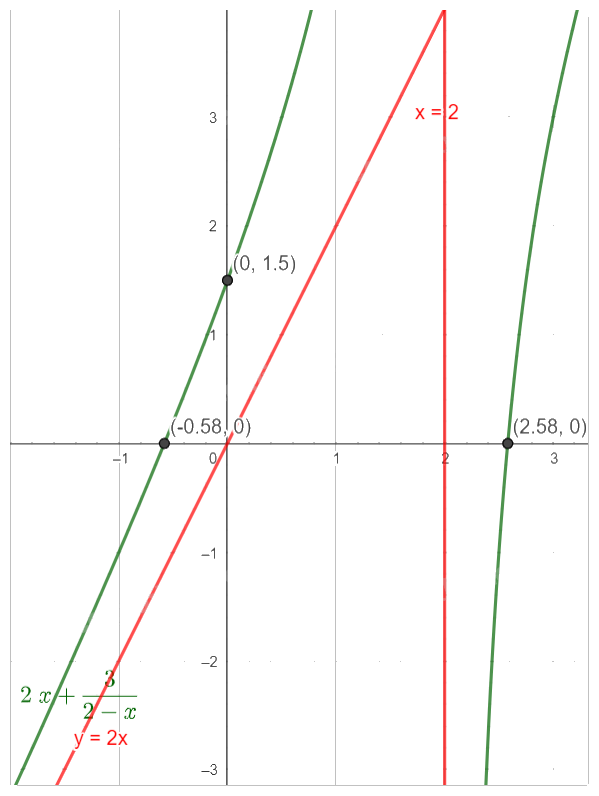
- Vẽ đồ thị
Giao điểm với trục Ox là \(\left( {\frac{{2 + \sqrt {10} }}{2};0} \right),\left( {\frac{{2 - \sqrt {10} }}{2};0} \right)\)
Giao điểm với trục Oy là \(\left( {0;\frac{3}{2}} \right)\)
Bài tập 1.35 trang 46 SGK Toán 12 tập 1 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và quy tắc đạo hàm của hàm hợp để giải quyết.
Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài tập 1.35 yêu cầu tìm đạo hàm của hàm số f(x) = x2 + 3x - 2. Chúng ta sẽ thực hiện như sau:
Vậy, đạo hàm của hàm số f(x) = x2 + 3x - 2 là f'(x) = 2x + 3.
Ngoài bài tập 1.35, còn rất nhiều dạng bài tập khác liên quan đến đạo hàm mà học sinh cần nắm vững. Một số dạng bài tập thường gặp bao gồm:
Để giải bài tập về đạo hàm một cách chính xác và hiệu quả, học sinh cần lưu ý một số điều sau:
Kết luận:
Bài tập 1.35 trang 46 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
| f(x) = ex | f'(x) = ex |
| f(x) = ln(x) | f'(x) = 1/x |