Chào mừng các em học sinh đến với bài giải bài tập 1.18 trang 22 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán về đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.
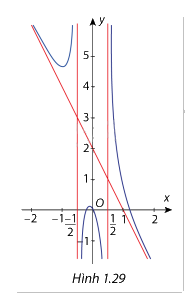
Cho hàm số xác định trên và có đô thị là các phần đường cong như Hình 1.29. Xác định phương trình đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên( nếu có) của đồ thị hàm số đã cho.
Đề bài
Cho hàm số xác định trên và có đô thị là các phần đường cong như Hình 1.29. Xác định phương trình đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên( nếu có) của đồ thị hàm số đã cho.
Phương pháp giải - Xem chi tiết
Nhìn đồ thị hàm số rồi nhận xét.
Lời giải chi tiết
Dựa vào dồ thị hàm số ta thấy:
Đường thẳng x = \(\frac{1}{2}\) và x = \( - \frac{1}{2}\) là đường tiệm đứng của đồ thị hàm số đã cho.
Tiệm cận xiên cảu hàm số đã cho đi qua 2 điểm (0;2) và (1;0) nên đường tiệm xiên của hàm số có phương trình là y = - 2x + 2.
Bài tập 1.18 trang 22 SGK Toán 12 tập 1 thường liên quan đến việc tìm đạo hàm của hàm số và sử dụng đạo hàm để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài tập 1.18. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và giải bài tập, chúng ta có thể đưa ra một phương pháp tiếp cận chung:
Giả sử bài tập 1.18 yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1. Ta thực hiện như sau:
f'(x) = 3x2 - 6x + 2
Để tìm cực trị của hàm số, ta giải phương trình f'(x) = 0:
3x2 - 6x + 2 = 0
Giải phương trình bậc hai này, ta tìm được hai nghiệm x1 và x2. Đây là các điểm cực trị của hàm số.
Ngoài việc giải bài tập 1.18, các em có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong các lĩnh vực khác nhau, như vật lý, kinh tế, kỹ thuật. Ví dụ, đạo hàm có thể được sử dụng để tính vận tốc, gia tốc của một vật thể chuyển động, hoặc để tối ưu hóa lợi nhuận của một doanh nghiệp.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ của giáo viên và bạn bè.
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin x | y' = cos x |
| y = cos x | y' = -sin x |
Bài tập 1.18 trang 22 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em rèn luyện kỹ năng giải bài tập về đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và phương pháp giải bài tập, các em có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.