Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 67 và 68 sách giáo khoa Toán 12 tập 2.
Mục tiêu của chúng ta là nắm vững kiến thức, hiểu rõ phương pháp giải và đạt kết quả tốt nhất trong các bài kiểm tra và kỳ thi sắp tới.
Cho hai vectơ ngược hướng (vec a) và (vec b) là hai vectơ chỉ phương của đường thẳng (d) và (vec a') là vectơ chỉ phương của đường thẳng (d')(Hình 5.26). Cho biết ((d,d') = {45^{^circ }}). Hãy tính số đo của hai góc: (left( {vec a,vec a'} right)) và ((vec b,vec a')). Từ đó chỉ ra mối quan hệ giữa hai góc ((d,d')) và ((vec a,vec a')), giữa (cos (d,d')) và (cos (vec a,vec a')).
Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa hai đường thẳng d và d' trong các trường hợp sau:
a) \(d:\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\) và \(d':\frac{{x - 1}}{4} = \frac{y}{2} = \frac{{z + 1}}{2}\)
b) \(d:\frac{x}{2} = \frac{y}{{ - 4}} = \frac{z}{5}\) và \(d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 2 - t\;\\y = 3 + 2t\;\\z = 2t\end{array}\end{array}} \right.\) \((t \in \mathbb{R})\)
Phương pháp giải:
Xác định vector chỉ phương của mỗi đường thẳng.
Sử dụng công thức cosin góc giữa hai vector: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a||\vec b|}}\).
Tính góc từ giá trị cosin.
Lời giải chi tiết:
a)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (3,4,5)\)
\(d':\overrightarrow {{a_2}} = (4,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{3 \cdot 4 + 4 \cdot 2 + 5 \cdot 2}}{{\sqrt {({3^2} + {4^2} + {5^2})({4^2} + {2^2} + {2^2})} }}\)
\( = \frac{{12 + 8 + 10}}{{\sqrt {(9 + 16 + 25)(16 + 4 + 4)} }}\)
\( = \frac{{30}}{{\sqrt {50 \cdot 24} }}\)
\( = \frac{3}{{\sqrt 2 }}\)
Suy ra góc \(\phi = 30^\circ \)
b)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (2, - 4,5)\)
\(d':\overrightarrow {{a_2}} = ( - 1,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{2 \cdot ( - 1) + ( - 4) \cdot 2 + 5 \cdot 2}}{{\sqrt {({2^2} + {{( - 4)}^2} + {5^2})({{( - 1)}^2} + {2^2} + {2^2})} }}\)
\( = \frac{{ - 2 - 8 + 10}}{{\sqrt {(4 + 16 + 25)(1 + 4 + 4)} }}\)
\( = \frac{0}{{\sqrt {45 \cdot 9} }}\)
\( = 0\)
Do \(\cos (\phi ) = 0\), nên \(\phi = 90^\circ \)
Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 12 Cùng khám phá
Cho hai vectơ ngược hướng \(\vec a\) và \(\vec b\) là hai vectơ chỉ phương của đường thẳng \(d\) và \(\vec a'\) là vectơ chỉ phương của đường thẳng \(d'\)(Hình 5.26). Cho biết \((d,d') = {45^{^\circ }}\). Hãy tính số đo của hai góc: \(\left( {\vec a,\vec a'} \right)\) và \((\vec b,\vec a')\). Từ đó chỉ ra mối quan hệ giữa hai góc \((d,d')\) và \((\vec a,\vec a')\), giữa \(\cos (d,d')\) và \(\cos (\vec a,\vec a')\).
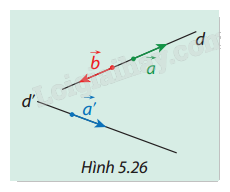
Phương pháp giải:
Sử dụng tích vô hướng của hai vectơ để tính góc giữa chúng:
\(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\)
Lời giải chi tiết:
- Góc giữa \(\vec a\) và \(\vec a'\):
Ta sử dụng công thức cosin cho góc giữa hai vectơ:
\(\cos (\vec a,\vec a') = \frac{{\vec a \cdot \vec a'}}{{\left| {\vec a} \right|.\left| {\vec a'} \right|}} = \frac{{{a_1}{{a'}_1} + {a_2}{{a'}_2} + {a_3}{{a'}_3}}}{{\sqrt {(a_1^2 + a_2^2 + a_3^2)({a_1}{'^2} + {a_2}{'^2} + {a_3}{'^2})} }}\)
Biết rằng \((d,d') = {45^\circ }\) và Vì \(\overrightarrow a \) là vector chỉ phương của d và \(\overrightarrow {a'} \) là vector chỉ phương của d' nên góc giữa hai vector bằng góc giữa hai đường thẳng. Suy ra góc giữa \(\vec a\) và \(\vec a'\) là \({45^\circ }\).
- Góc giữa \(\vec b\) và \(\vec a'\):
Vì \(\vec b = - \vec a\), ta có:
\(\cos \left( {\vec b,\vec a'} \right) = \cos \left( { - \vec a,\vec a'} \right) = - \cos \left( {\vec a,\vec a'} \right) = - \cos 45^\circ \)
Suy ra:
\(\cos \left( {\vec b,\vec a'} \right) = - \frac{1}{{\sqrt 2 }}\)
Do đó, góc giữa \(\vec b\) và \(\vec a'\) là \({135^\circ }\).
- Mối quan hệ giữa hai góc:
Góc giữa hai đường thẳng \((d,d')\) và góc giữa hai vectơ chỉ phương \(\vec a\) và \(\vec a'\) bằng nhau, tức là: \((d,d') = \left( {\vec a,\vec a'} \right) = {45^\circ }\)
- Tương tự, mối quan hệ giữa \(\cos (d,d')\) và \(\cos \left( {\vec a,\vec a'} \right)\) là: \(\cos (d,d') = \cos \left( {\vec a,\vec a'} \right) = \frac{1}{{\sqrt 2 }}\)
Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa hai đường thẳng d và d' trong các trường hợp sau:
a) \(d:\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\) và \(d':\frac{{x - 1}}{4} = \frac{y}{2} = \frac{{z + 1}}{2}\)
b) \(d:\frac{x}{2} = \frac{y}{{ - 4}} = \frac{z}{5}\) và \(d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 2 - t\;\\y = 3 + 2t\;\\z = 2t\end{array}\end{array}} \right.\) \((t \in \mathbb{R})\)
Phương pháp giải:
Xác định vector chỉ phương của mỗi đường thẳng.
Sử dụng công thức cosin góc giữa hai vector: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a||\vec b|}}\).
Tính góc từ giá trị cosin.
Lời giải chi tiết:
a)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (3,4,5)\)
\(d':\overrightarrow {{a_2}} = (4,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{3 \cdot 4 + 4 \cdot 2 + 5 \cdot 2}}{{\sqrt {({3^2} + {4^2} + {5^2})({4^2} + {2^2} + {2^2})} }}\)
\( = \frac{{12 + 8 + 10}}{{\sqrt {(9 + 16 + 25)(16 + 4 + 4)} }}\)
\( = \frac{{30}}{{\sqrt {50 \cdot 24} }}\)
\( = \frac{3}{{\sqrt 2 }}\)
Suy ra góc \(\phi = 30^\circ \)
b)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (2, - 4,5)\)
\(d':\overrightarrow {{a_2}} = ( - 1,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{2 \cdot ( - 1) + ( - 4) \cdot 2 + 5 \cdot 2}}{{\sqrt {({2^2} + {{( - 4)}^2} + {5^2})({{( - 1)}^2} + {2^2} + {2^2})} }}\)
\( = \frac{{ - 2 - 8 + 10}}{{\sqrt {(4 + 16 + 25)(1 + 4 + 4)} }}\)
\( = \frac{0}{{\sqrt {45 \cdot 9} }}\)
\( = 0\)
Do \(\cos (\phi ) = 0\), nên \(\phi = 90^\circ \)
Mục 1 của SGK Toán 12 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là nền tảng để hiểu sâu hơn các kiến thức tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 1 trang 67 và 68, giúp các em học sinh tự tin hơn trong quá trình học tập.
Để hiểu rõ hơn về mục 1 trang 67, 68, chúng ta cần xác định rõ nội dung chính mà SGK Toán 12 tập 2 muốn truyền tải. Thông thường, mục này sẽ bao gồm các kiến thức lý thuyết cơ bản, các ví dụ minh họa và các bài tập vận dụng. Việc nắm vững các kiến thức lý thuyết là bước đầu tiên để giải quyết các bài tập một cách hiệu quả.
Bài tập 1 thường là bài tập khởi động, giúp các em học sinh ôn lại kiến thức cũ và làm quen với dạng bài tập mới. Để giải bài tập này, chúng ta cần…
Bài tập 2 thường là bài tập vận dụng kiến thức lý thuyết vào giải quyết các vấn đề thực tế. Để giải bài tập này, chúng ta cần…
Bài tập 3 thường là bài tập nâng cao, đòi hỏi các em học sinh phải có khả năng tư duy logic và vận dụng linh hoạt các kiến thức đã học. Để giải bài tập này, chúng ta cần…
Bài tập 4 thường là bài tập tổng hợp, giúp các em học sinh củng cố kiến thức và kỹ năng đã học. Để giải bài tập này, chúng ta cần…
Kiến thức trong mục 1 trang 67, 68 có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kinh tế, kỹ thuật và khoa học. Việc nắm vững kiến thức này sẽ giúp các em học sinh có lợi thế trong quá trình học tập và làm việc sau này.
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 67, 68 SGK Toán 12 tập 2 một cách hiệu quả. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!