Chào mừng bạn đến với chuyên mục Lý thuyết Góc Toán 12 của giaitoan.edu.vn! Đây là nơi bạn có thể tìm thấy mọi kiến thức cần thiết về góc, từ định nghĩa cơ bản đến các ứng dụng nâng cao trong chương trình Toán 12.
Chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
1. Góc giữa hai đường thẳng
1. Góc giữa hai đường thẳng
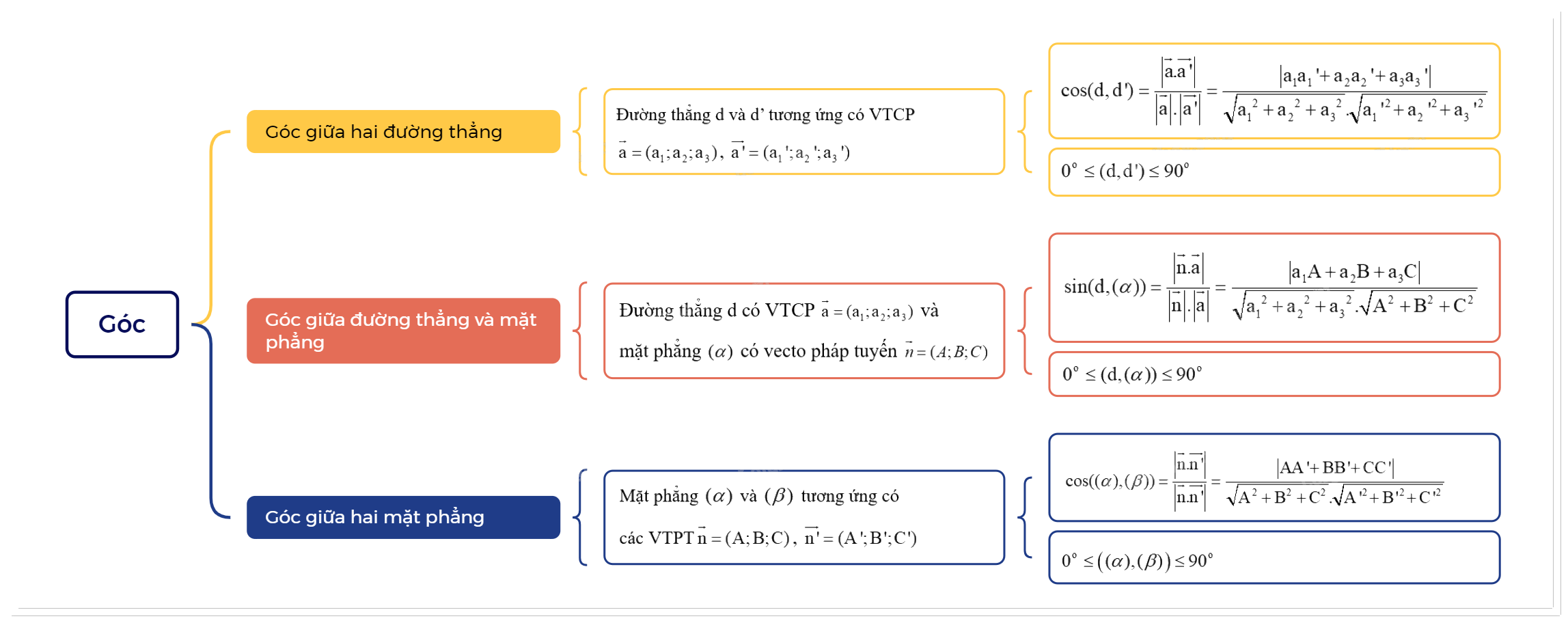
Trong không gian Oxyz, cho hai đường thẳng d và d’ tương ứng có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow {a'} = ({a_1}';{a_2}';{a_3}')\). Khi đó: \(\cos (d,d') = \frac{{\left| {\overrightarrow a .\overrightarrow {a'} } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow {a'} } \right|}} = \frac{{\left| {{a_1}{a_1}' + {a_2}{a_2}' + {a_3}{a_3}'} \right|}}{{\sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} .\sqrt {{a_1}{'^2} + {a_2}{'^2} + {a_3}{'^2}} }}\) |
Lưu ý:
+ \({0^o} \le (d,d') \le {90^o}\).
+ Nếu d//d’ hoặc d\( \equiv \)d’ thì \((d,d') = {0^o}\).
+ \(d \bot d' \Leftrightarrow (d,d') = {90^o}\).
Ví dụ: Trong không gian Oxyz, tính góc giữa hai đường thẳng:
d: \(\left\{ \begin{array}{l}x = 1 + t\\y = 3 - t\\z = 2t\end{array} \right.\) \((t \in \mathbb{R})\) và d’: \(\left\{ \begin{array}{l}x = t'\\y = 1 + 2t'\\z = 3 - t'\end{array} \right.\) \((t' \in \mathbb{R})\).
Giải:
Đường thẳng d và d’ lần lượt có các vecto chỉ phương là \(\overrightarrow a = (1; - 1;2)\) và \(\overrightarrow {a'} = (1;2; - 1)\).
Ta có \(\cos (d,d') = \frac{{\left| {\overrightarrow a .\overrightarrow {a'} } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow {a'} } \right|}} = \frac{{\left| {1.1 - 1.2 + 2.( - 1)} \right|}}{{\sqrt {{1^2} + {{( - 1)}^2} + {2^2}} .\sqrt {{1^2} + {2^2} + {{( - 1)}^2}} }} = \frac{{\left| { - 3} \right|}}{6} = \frac{1}{2}\).
Vậy \((d,d') = {60^o}\).
2. Góc giữa đường thẳng và mặt phẳng
Trong không gian Oxyz, cho đường thẳng d có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\) và mặt phẳng \((\alpha )\) có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\). Kí hiệu \(\left( {d,(\alpha )} \right)\) là góc giữa đường thẳng d và mặt phẳng \((\alpha )\). Khi đó: \(\sin (d,(\alpha )) = \frac{{\left| {\overrightarrow n .\overrightarrow a } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow a } \right|}} = \frac{{\left| {{a_1}A + {a_2}B + {a_3}C} \right|}}{{\sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} .\sqrt {{A^2} + {B^2} + {C^2}} }}\). |
Lưu ý:
+ \({0^o} \le (d,(\alpha )) \le {90^o}\).
+ Nếu \(d//(\alpha )\) hoặc \(d \subset (\alpha )\) thì \((d,(\alpha )) = {0^o}\).
+ \(d \bot (\alpha ) \Leftrightarrow (d,(\alpha )) = {90^o}\).
Ví dụ: Trong không gian Oxyz, tính góc giữa đường thẳng d: \(\frac{x}{{ - 1}} = \frac{y}{2} = \frac{{z - 1}}{{ - 1}}\) và mặt phẳng \((\alpha )\): \(x + y - 2z + 1 = 0\).
Giải:
Đường thẳng d có vectơ chỉ phương \(\overrightarrow a = ( - 1;2; - 1)\), mặt phẳng \((\alpha )\) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;1; - 2} \right)\).
Ta có: \(\sin (d,(\alpha )) = \frac{{\left| {\overrightarrow n .\overrightarrow a } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow a } \right|}} = \frac{{\left| {( - 1).1 + 2.1( - 1).( - 2)} \right|}}{{\sqrt {{{( - 1)}^2} + {2^2} + {{( - 1)}^2}} .\sqrt {{1^2} + {1^2} + {{( - 2)}^2}} }} = \frac{1}{2}\).
Vậy \((d,(\alpha )) = {30^o}\).
3. Góc giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng \((\alpha )\) và \((\beta )\) tương ứng có các vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\). Khi đó, góc giữa \((\alpha )\) và \((\beta )\), kí hiệu là \(\left( {(\alpha ),(\beta )} \right)\) được tính theo công thức: \(\cos ((\alpha ),(\beta )) = \frac{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}}{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}} = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\). |
Lưu ý:
+ \({0^o} \le \left( {(\alpha ),(\beta )} \right) \le {90^o}\).
+ Nếu \((\alpha )\)//\((\beta )\) hoặc \((\alpha ) \equiv (\beta )\) thì \(\left( {(\alpha ),(\beta )} \right) = {0^o}\).
+ \((\alpha ) \bot (\beta ) \Leftrightarrow \left( {(\alpha ),(\beta )} \right) = {90^o}\).
Ví dụ: Trong không gian Oxyz, tính góc giữa hai mặt phẳng: :\((\alpha )\) \(2x + 2y - 4z + 1 = 0\) và \((\beta )\): \(x - z - 5 = 0\).
Giải:
Mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\overrightarrow n = (2;2; - 4)\) và \(\overrightarrow {n'} = (1;0; - 1)\).
Ta có: \(\cos ((\alpha ),(\beta )) = \frac{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}}{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}} = \frac{{\left| {2.1 + 2.0 + ( - 4).( - 1)} \right|}}{{\sqrt {{2^2} + {2^2} + {{( - 4)}^2}} .\sqrt {{1^2} + {0^2} + {{( - 1)}^2}} }} = \frac{{\sqrt 3 }}{2}\).
Vậy \(\left( {(\alpha ),(\beta )} \right) = {30^o}\).
Trong chương trình Toán 12, kiến thức về góc đóng vai trò vô cùng quan trọng, đặc biệt trong các chủ đề như lượng giác, đường thẳng và mặt phẳng, và hình học không gian. Việc nắm vững lý thuyết góc không chỉ giúp bạn giải quyết các bài toán một cách chính xác mà còn là nền tảng để tiếp thu các kiến thức nâng cao hơn.
Góc là hình được tạo bởi hai tia chung gốc. Dưới đây là các loại góc cơ bản:
Góc thường được đo bằng độ (°). Một vòng tròn đầy đủ là 360 độ. Ngoài độ, góc còn có thể được đo bằng radian (rad). Mối quan hệ giữa độ và radian là:
180° = π rad
Góc lượng giác là góc được xác định bởi một đường tròn lượng giác. Các hàm lượng giác (sin, cos, tan, cot) được định nghĩa dựa trên góc lượng giác và có vai trò quan trọng trong việc giải các bài toán liên quan đến tam giác, dao động điều hòa và nhiều lĩnh vực khác.
| Hàm lượng giác | Công thức |
|---|---|
| sin(α) | Đối diện / Cạnh huyền |
| cos(α) | Kề / Cạnh huyền |
| tan(α) | Đối diện / Kề |
| cot(α) | Kề / Đối diện |
Lý thuyết góc được ứng dụng rộng rãi trong các chủ đề sau:
Để củng cố kiến thức về lý thuyết góc, bạn có thể thực hành các bài tập sau:
Lý thuyết Góc Toán 12 là một phần kiến thức quan trọng trong chương trình Toán 12. Việc nắm vững lý thuyết này sẽ giúp bạn tự tin giải quyết các bài toán và đạt kết quả tốt trong kỳ thi. Hãy dành thời gian ôn tập và thực hành để hiểu sâu sắc về các khái niệm và công thức liên quan đến góc.