Chào mừng các em học sinh đến với bài giải bài tập 4.15 trang 20 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
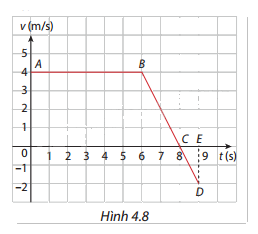
Đường gấp khúc ABD trong Hình 4.8 là đồ thị vận tốc \(v(t)\) của một vật (t = 0 là thời điểm vật bắt đầu chuyển động). Trong khoảng thời gian mà \(v < 0\)thì vật chuyển động ngược chiều với khoảng thời gian mà \(v > 0\). a) Viết công thức của hàm số \(v(t)\) với \(t \in [0;9]\). b) Biết rằng quãng đường vật đi chuyển với vận tốc \(v = v(t)\) từ thời điểm \(t = a\) đến thời điểm \(t = b\) là \(s = \int_a^b | v(t)|{\mkern 1mu} dt\), tính quãng đường vật di chuyển được trong 9 giây kể từ khi vật
Đề bài
Đường gấp khúc ABD trong Hình 4.8 là đồ thị vận tốc \(v(t)\) của một vật (t = 0 là thời điểm vật bắt đầu chuyển động). Trong khoảng thời gian mà \(v < 0\)thì vật chuyển động ngược chiều với khoảng thời gian mà \(v > 0\).
a) Viết công thức của hàm số \(v(t)\) với \(t \in [0;9]\).
b) Biết rằng quãng đường vật đi chuyển với vận tốc \(v = v(t)\) từ thời điểm \(t = a\) đến thời điểm \(t = b\) là \(s = \int_a^b | v(t)|{\mkern 1mu} dt\), tính quãng đường vật di chuyển được trong 9 giây kể từ khi vật bắt đầu chuyển động.
c) Tính tổng diện tích của hình thang \(OABC\) và tam giác \(CDE\) rồi so sánh với kết quả ở câu b.
Phương pháp giải - Xem chi tiết
a)
- Xác định các đoạn của đồ thị: Đồ thị gồm các đoạn AB, BC, và CD.
b)
- Sử dụng công thức tính quãng đường từ \(t = 0\) đến \(t = 9\) bằng tích phân của \(|v(t)|\).
- Tính từng phần diện tích tương ứng với các đoạn AB, BC, CD trên đồ thị.
c)
- Diện tích hình thang \(OABC\) được tính theo công thức diện tích hình thang.
- Diện tích tam giác \(CDE\) được tính theo công thức diện tích tam giác.
Lời giải chi tiết
a)
- Đoạn \(AB\): Ở đây, đồ thị có giá trị vận tốc không đổi là 4 m/s từ \(t = 0\) đến \(t = 6\), tức là:
\(v(t) = 4\quad {\rm{,}}\quad t \in [0;6].\)
- Đoạn \(BC\) và \(CD\): Đoạn này là một đường thẳng dốc xuống từ \(t = 6\) đến \(t = 8\), vận tốc giảm từ 4 m/s xuống -2 m/s. Phương trình đường thẳng có dạng:
\(v(t) = - 2t + 16\,\,\,\,\,\,{\rm{,}}\quad t \in [6;9].\)
Vậy, công thức của hàm vận tốc \(v(t)\) theo từng khoảng là:
\(v(t) = \mathop \{ \nolimits_{ - 2t + 16\,\,\,\,\,\,khi\,\,6 < t \le 9}^{4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,0 \le t \le 6} \)
b)
- Quãng đường được tính là tích phân của \(|v(t)|\). Cần tính tích phân của các đoạn như sau:
Đoạn AB:
\(\int_0^6 | v(t)|dt = \int_0^6 4 {\mkern 1mu} dt = 4 \times 6 = 24{\mkern 1mu} {\rm{m}}.\)
Đoạn BC và CD:
\(\int_6^9 | v(t)|dt = \int_6^9 {\left| { - 2t + 16} \right|} dt = \int_6^8 {\left( { - 2t + 16} \right)dt + } \int_8^9 {\left( {2t - 16} \right)dt} \)
\(\int_6^9 | v(t)|dt = \left. {( - {t^2} + 16t)} \right|_6^8 + \left. {({t^2} - 16t)} \right|_8^9 = 4 + 1 = 5m\)
Tổng quãng đường vật di chuyển là:
\(24 + 5 = 29{\mkern 1mu} {\rm{m}}.\)
c)
Diện tích hình thang \(OABC\):
Công thức diện tích hình thang:
\({S_{{\rm{ht}}}} = \frac{1}{2} \times (AB + OC) \times OA = \frac{1}{2} \times (6 + 8) \times 4 = 28{\mkern 1mu} .\)
Diện tích tam giác \(CDE\):
Công thức diện tích tam giác:
\({S_{{\rm{tg}}}} = \frac{1}{2} \times CE \times ED = \frac{1}{2} \times 1 \times 2 = 1{\mkern 1mu} \)
Tổng diện tích là:
\({S_{{\rm{tong}}}} = 28 + 1 = 29\)
Vậy kết quả ở câu c và câu b là giống nhau.
Bài tập 4.15 trang 20 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để tìm cực trị, khoảng đơn điệu và vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý liên quan đến đạo hàm.
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy:
1. Tập xác định của hàm số:
Hàm số y = f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R.
2. Tính đạo hàm f'(x):
f'(x) = 3x2 - 6x
3. Tìm các điểm cực trị của hàm số:
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Ta xét dấu của f'(x) trên các khoảng:
Vậy, hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
4. Xác định khoảng đơn điệu của hàm số:
Dựa vào bảng xét dấu của f'(x), ta có:
5. Vẽ đồ thị hàm số:
Để vẽ đồ thị hàm số, ta cần xác định các điểm đặc biệt như:
Dựa vào các điểm này và khoảng đơn điệu của hàm số, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Để củng cố kiến thức về đạo hàm, các em có thể tham khảo các bài tập tương tự sau:
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 4.15 trang 20 SGK Toán 12 tập 2 và tự tin hơn trong quá trình học tập. Chúc các em học tốt!