Chào mừng các em học sinh đến với bài giải bài tập 1.43 trang 48 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như Bảng 1.5. Khẳng định nào sau đây đúng?
Đề bài
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như Bảng 1.5. Khẳng định nào sau đây đúng?
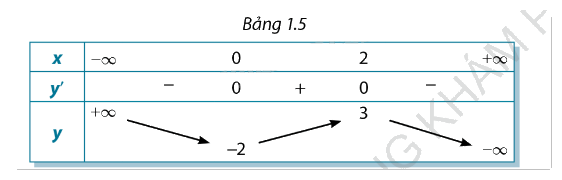
A. Hàm số đồng biến trên \((0;2)\) và đạt cực đại tại \(x = 2\).
B. Hàm số đồng biến trên \((0;2)\) và đạt cực đại tại \(x = 0\).
C. Hàm số nghịch biến trên \((0;2)\) và đạt cực đại tại \(x = 2\).
D. Hàm số nghịch biến trên \((0;2)\) và đạt cực đại tại \(x = 0\).
Phương pháp giải - Xem chi tiết
- Nếu trong một khoảng xác định, đạo hàm của hàm số mang dấu âm có nghĩa là hàm số nghịch biến trên khoảng đó. Ngược lại, nếu đạo hàm của hàm số mang dấu dương nghĩa là hàm số đồng biến trên khoảng đó.
- Điểm cực đại là điểm mà ngay tại đó, đồ thị hàm số chuyển từ đồng biến sang nghịch biến.
Lời giải chi tiết
Dựa vào bảng 1.5 có thể thấy trong khoảng (0;2) thì hàm số đồng biến và đạt cực đại tại \(x = 2\). → Chọn A.
Bài tập 1.43 trang 48 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2.
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
f'(x) = 3x2 - 6x.
Giải phương trình f'(x) = 0, ta được:
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
Vậy, hàm số có hai điểm dừng là x = 0 và x = 2.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta thấy:
limx→-∞ f(x) = -∞ và limx→+∞ f(x) = +∞.
Dựa trên các thông tin đã thu thập, ta có thể vẽ đồ thị hàm số f(x) = x3 - 3x2 + 2.
Việc giải bài tập 1.43 trang 48 SGK Toán 12 tập 1 không chỉ giúp chúng ta hiểu rõ hơn về cách khảo sát hàm số mà còn có ứng dụng thực tế trong nhiều lĩnh vực như kinh tế, kỹ thuật, và khoa học tự nhiên. Ví dụ, trong kinh tế, việc khảo sát hàm số chi phí có thể giúp doanh nghiệp tối ưu hóa sản lượng và lợi nhuận.
Hy vọng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập 1.43 trang 48 SGK Toán 12 tập 1 và tự tin hơn trong việc giải các bài tập tương tự. Chúc các em học tập tốt!