Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
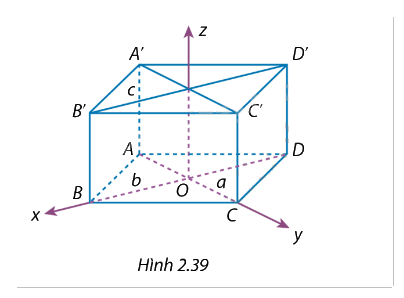
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định: a) Toạ độ các đỉnh của hình hộp; b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).
Đề bài
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định:
a) Toạ độ các đỉnh của hình hộp;
b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).
Phương pháp giải - Xem chi tiết
- Sử dụng gốc tọa độ tại giao điểm của hai đường chéo hình thoi, xác định tọa độ các đỉnh đáy dựa vào chiều dài các đường chéo.
- Dùng công thức \(\overrightarrow {XY} = ({x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1})\) để tìm tọa độ vectơ \(\overrightarrow {BD'} \).
Lời giải chi tiết
a) Xác định tọa độ các đỉnh của hình hộp.
\(B\left( {\frac{b}{2},0,0} \right),{\rm{ }}A\left( {0,\frac{{ - a}}{2},0} \right),C\left( {0,\frac{a}{2},0} \right){\rm{, }}D\left( {\frac{{ - b}}{2},0,0} \right)\)
Tọa độ của các đỉnh A', B', C', D' lần lượt là:
\(B'\left( {\frac{b}{2},0,c} \right),{\rm{ }}A'\left( {0,\frac{{ - a}}{2},c} \right),C'\left( {0,\frac{a}{2},c} \right){\rm{, }}D'\left( {\frac{{ - b}}{2},0,c} \right)\)
b) Tọa độ vectơ \(\overrightarrow {BD'} :\)
\(\overrightarrow {BD'} = D' - B = ( - \frac{b}{2},0,c) - (\frac{b}{2},0,0) = ( - b,0,c)\)
Bài tập 2.14 trang 73 SGK Toán 12 tập 1 thuộc chương trình học về đạo hàm. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm của hàm số, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 2.14 thường yêu cầu học sinh tìm đạo hàm của một hàm số, xét dấu đạo hàm để xác định khoảng đơn điệu của hàm số, hoặc tìm cực trị của hàm số.
Giả sử bài tập 2.14 yêu cầu: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Giải:
Đạo hàm không chỉ là một công cụ quan trọng trong toán học mà còn có nhiều ứng dụng trong thực tế, như:
Bài tập 2.14 trang 73 SGK Toán 12 tập 1 là một bài tập điển hình về ứng dụng của đạo hàm trong việc tìm cực trị và khoảng đơn điệu của hàm số. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài tập và nắm vững kiến thức về đạo hàm. Hãy tiếp tục luyện tập và khám phá thêm nhiều bài tập khác để nâng cao kỹ năng giải toán của mình.
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của hằng số | (c)' = 0 |
| Đạo hàm của xn | (xn)' = nxn-1 |
| Đạo hàm của u + v | (u + v)' = u' + v' |