Chào mừng các em học sinh đến với bài giải bài tập 5.33 trang 77 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Bạn Bình đố bạn Nam tìm được đường kính của quả bóng rổ, biết rằng nếu đặt quả bóng ở một góc căn phòng hình hộp chữ nhật, sao cho quả bóng chạm (tiếp xúc) với hai bức tường và nền nhà của căn phòng đó (khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng) thì có một điểm M trên quả bóng với khoảng cách lần lượt đến hai bức tường và nền nhà là 17 cm, 18 cm và 21 cm (Hình 5.38). Hãy giúp Nam xác định đường kính của quả bóng rổ. Biết rằng loại bóng rổ tiêu chuẩn
Đề bài
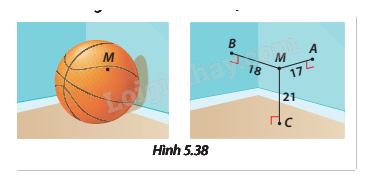
Bạn Bình đố bạn Nam tìm được đường kính của quả bóng rổ, biết rằng nếu đặt quả bóng ở một góc căn phòng hình hộp chữ nhật, sao cho quả bóng chạm (tiếp xúc) với hai bức tường và nền nhà của căn phòng đó (khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng) thì có một điểm M trên quả bóng với khoảng cách lần lượt đến hai bức tường và nền nhà là 17 cm, 18 cm và 21 cm (Hình 5.38).
Hãy giúp Nam xác định đường kính của quả bóng rổ. Biết rằng loại bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm.
Phương pháp giải - Xem chi tiết
- Xác định gốc toạ độ từ đó suy ra toạ độ của điểm M và tâm của quả bóng.
- Tính bán kính của quả bóng dựa trên các dữ kiện liên quan đến bán kính được cho ở đề bài.
Lời giải chi tiết
Đặt toạ độ O tại vị trí giao nhau giữa hai bức tường và nền nhà.
Toạ độ tương ứng với điểm M là \((17;18;21)\)
Gọi \(I(x;y;z)\) là tâm của quả bóng.
Vì khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng nên ta có: \(r = x = y = z\)
Suy ra I có toạ độ là \(I(r;r;r)\)
Do M nằm trên bề mặt quả bóng nên khoảng cách từ tâm I của quả bóng tới M chính là bán kính r, nên:
\(\begin{array}{l}\sqrt {{{(r - 17)}^2} + {{(r - 18)}^2} + {{(r - 21)}^2}} = r\\ \Leftrightarrow {r^2} - 34r + 289 + {r^2} - 36r + 324 + {r^2} - 42r + 441 = {r^2}\\ \Leftrightarrow 2{r^2} - 112r + 1054 = 0\end{array}\)
Từ phương trình trên ta thu được hai giá trị \({r_1} \approx 44,03\)và \({r_2} \approx 11,97\).
Vì loại bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm nên ta loại giá trị \({r_1}\) và nhận giá trị \({r_2}\) làm bán kính của quả bóng.
Vậy đường kính của bóng rổ là 23,94 cm.
Bài tập 5.33 trang 77 SGK Toán 12 tập 2 là một bài toán điển hình về ứng dụng của đạo hàm để tìm cực trị của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, cũng như các phương pháp xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
Đề bài yêu cầu chúng ta tìm giá trị của tham số m để hàm số f(x) = x3 - 3mx2 + 2m3 có cực đại, cực tiểu và thỏa mãn điều kiện cho trước. Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:
Bước 1: Tính đạo hàm bậc nhất
Ta có: f'(x) = 3x2 - 6mx
Bước 2: Tìm các điểm cực trị
Giải phương trình f'(x) = 0, ta được:
3x2 - 6mx = 0
3x(x - 2m) = 0
Vậy, phương trình có hai nghiệm: x = 0 và x = 2m
Bước 3: Xác định điều kiện để hàm số có cực đại, cực tiểu
Để hàm số có cực đại, cực tiểu thì phương trình f'(x) = 0 phải có hai nghiệm phân biệt. Điều này xảy ra khi 0 ≠ 2m, tức là m ≠ 0.
Bước 4: Áp dụng điều kiện đề bài để tìm giá trị của m
Đề bài yêu cầu hàm số có cực đại, cực tiểu. Chúng ta đã xác định điều kiện m ≠ 0. Để đảm bảo điều kiện này, ta cần loại bỏ giá trị m = 0.
Vậy, giá trị của m cần tìm là m ≠ 0.
Để củng cố kiến thức về ứng dụng của đạo hàm, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 2 và các tài liệu luyện thi THPT Quốc gia. Việc luyện tập thường xuyên sẽ giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Đạo hàm không chỉ là một công cụ quan trọng trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác như vật lý, kinh tế, kỹ thuật,... Ví dụ, đạo hàm có thể được sử dụng để tính vận tốc, gia tốc của một vật thể chuyển động, hoặc để tối ưu hóa lợi nhuận của một doanh nghiệp.
Bài tập 5.33 trang 77 SGK Toán 12 tập 2 là một bài toán quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Hy vọng với lời giải chi tiết và những lưu ý quan trọng trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.