Bài tập 1.26 trang 36 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học Toán 12. Bài tập này thuộc chủ đề về hàm số và đồ thị, đòi hỏi học sinh phải nắm vững kiến thức về các loại hàm số, cách vẽ đồ thị và các tính chất của đồ thị.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập 1.26 trang 36 SGK Toán 12 tập 1, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
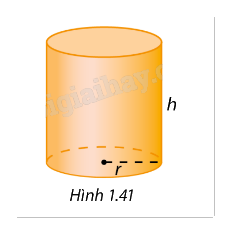
Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít (Hình 1.41). Tính tỉ lệ chiều cao và bán kính đáy hình trụ này để tổng chi phí làm vỏ lon (bao gồm cả hai đáy) là nhỏ nhất.
Đề bài
Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít (Hình 1.41). Tính tỉ lệ chiều cao và bán kính đáy hình trụ này để tổng chi phí làm vỏ lon (bao gồm cả hai đáy) là nhỏ nhất.
Phương pháp giải - Xem chi tiết
- Đặt bán kính đáy là 𝑟 và chiều cao là ℎ của hình trụ.
- Tính diện tích toàn phần của hình trụ dựa trên bán kính và chiều cao.
- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.
- Khảo sát hàm chi phí để tìm giá trị tối ưu.
Lời giải chi tiết
Gọi bán kính đáy là 𝑟 (𝑟 >0) và chiều cao là ℎ (ℎ>0) của hình trụ.
Thể tích hình trụ: \(V = \pi {r^2}h = 1000(c{m^3})\)
Diện tích xung quanh của hình trụ là: \({A_{xq}} = 2\pi rh\)
Diện tích của hai đáy là: \({A_{2đáy}} = 2\pi {r^2}\)
Tổng diện tích bề mặt: \(A = {A_{xq}} + {A_{2d\'a y}} = 2\pi rh + 2\pi {r^2} = 2\pi r.\frac{{1000}}{{\pi {r^2}}} + 2\pi {r^2} = \frac{{2000}}{r} + 2\pi {r^2}\)
Tìm giá trị cực trị: \(f(r) = \frac{{2000}}{r} + 2\pi {r^2}\)
- Tính đạo hàm: \(f'(r) = - \frac{{2000}}{{{r^2}}} + 4\pi r\)
- Cho đạo hàm bằng 0: \( - \frac{{2000}}{{{r^2}}} + 4\pi r = 0 \Rightarrow 4\pi r = \frac{{2000}}{{{r^2}}} \Rightarrow {r^3} = \frac{{2000}}{{4\pi }} = \frac{{500}}{\pi } \Rightarrow r \simeq 5,42(cm)\)
Bảng biến thiên:
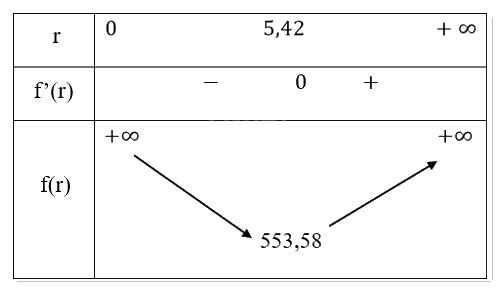
Nhận thấy f(r) đạt giá trị nhỏ nhất tại r ≈ 5,42
Vậy để tổng chi phí làm vỏ lon nhỏ nhất thì:
- Bán kính đáy của hình trụ: r ≈ 5,42 cm
- Chiều cao của hình trụ: \(h = \frac{{1000}}{{\pi {r^2}}} = \frac{{1000}}{{3,14.{{(5,42)}^2}}} \approx 10,84\)cm
- Tỉ lệ chiều cao và bán kính: \(\frac{h}{r} \approx \frac{{10,84}}{{5,42}} \approx 2\)
Bài tập 1.26 trang 36 SGK Toán 12 tập 1 thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm cực trị, hoặc vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể về bài tập 1.26 trang 36 SGK Toán 12 tập 1. Giả sử bài tập yêu cầu tìm khoảng đơn điệu của hàm số y = x3 - 3x2 + 2.
Vậy hàm số y = x3 - 3x2 + 2 đơn điệu tăng trên các khoảng (-∞, 0) và (2, +∞), đơn điệu giảm trên khoảng (0, 2).
Ngoài bài tập 1.26, SGK Toán 12 tập 1 còn có nhiều bài tập tương tự về hàm số và đồ thị. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức về hàm số và đồ thị, học sinh cần luyện tập thường xuyên các bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em học sinh rèn luyện kỹ năng giải toán và củng cố kiến thức đã học.
Kiến thức về hàm số và đồ thị là nền tảng quan trọng cho việc học các môn Toán cao cấp hơn. Việc nắm vững kiến thức này giúp học sinh hiểu rõ hơn về các khái niệm Toán học và ứng dụng chúng vào thực tế.
Bài tập 1.26 trang 36 SGK Toán 12 tập 1 là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng giải toán về hàm số và đồ thị. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải các bài tập tương tự.