Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 15 và 16 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu!
Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong ( Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y=1 khi \(x \to + \infty \) và \(x \to - \infty \).
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Cùng khám phá
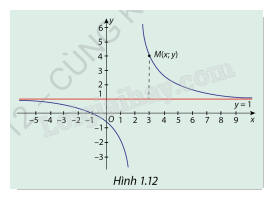
Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong ( Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y=1 khi \(x \to + \infty \) và \(x \to - \infty \).
Phương pháp giải:
Nhìn đồ thị hàm số rồi nhận xét.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy:
Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng y=1 càng nhỏ.
Trả lời câu hỏi Luyện tập 1 trang 16 SGK Toán 12 Cùng khám phá
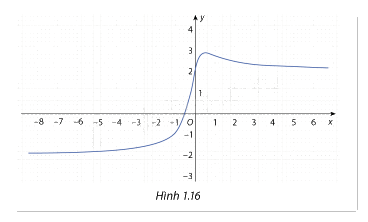
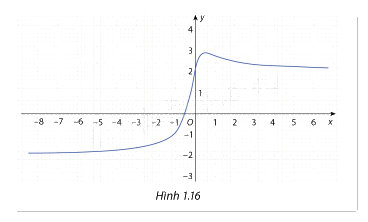
Cho hàm số \(y = f(x) = \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\) có đồ thị như Hình 1.16
a) Tìm các đường tiệm cận ngang của đô thị nếu có.
b) Vẽ các đường tiệm cận ngang vừa tìm được nếu có.
Phương pháp giải:
a) Xét \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to - \infty } f(x)\)
b) Trên trục Oy tại điểm có giá trị bằng 2 vẽ một đường thẳng song song với Ox. Trên trục Oy tại điểm có giá trị bằng -2 vẽ một đường thẳng song song với Ox.
Lời giải chi tiết:
a) Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = 2.
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = - 2.
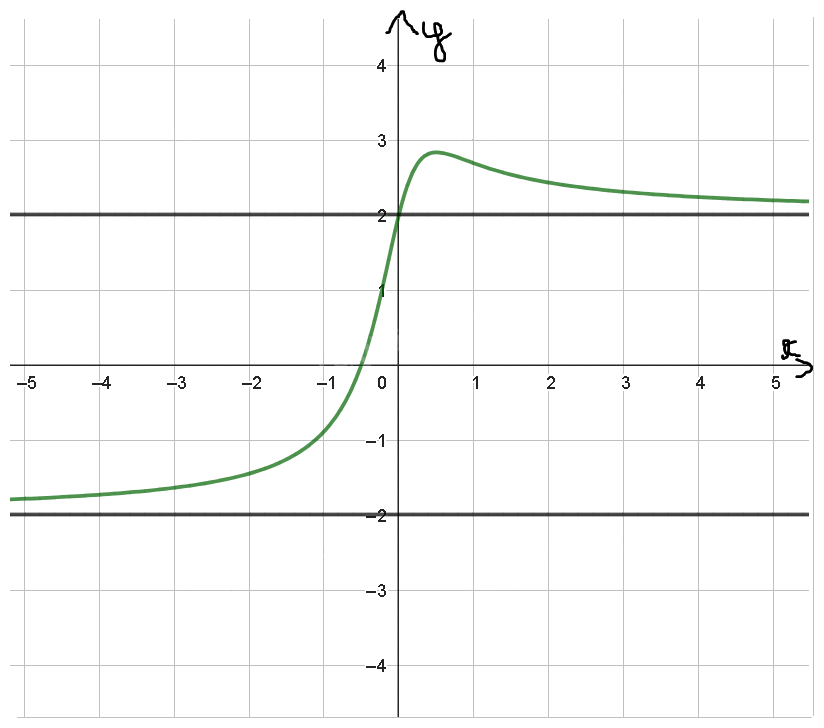
b)
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Cùng khám phá
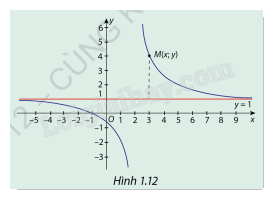
Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong ( Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y=1 khi \(x \to + \infty \) và \(x \to - \infty \).
Phương pháp giải:
Nhìn đồ thị hàm số rồi nhận xét.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy:
Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng y=1 càng nhỏ.
Trả lời câu hỏi Luyện tập 1 trang 16 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\) có đồ thị như Hình 1.16
a) Tìm các đường tiệm cận ngang của đô thị nếu có.
b) Vẽ các đường tiệm cận ngang vừa tìm được nếu có.
Phương pháp giải:
a) Xét \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to - \infty } f(x)\)
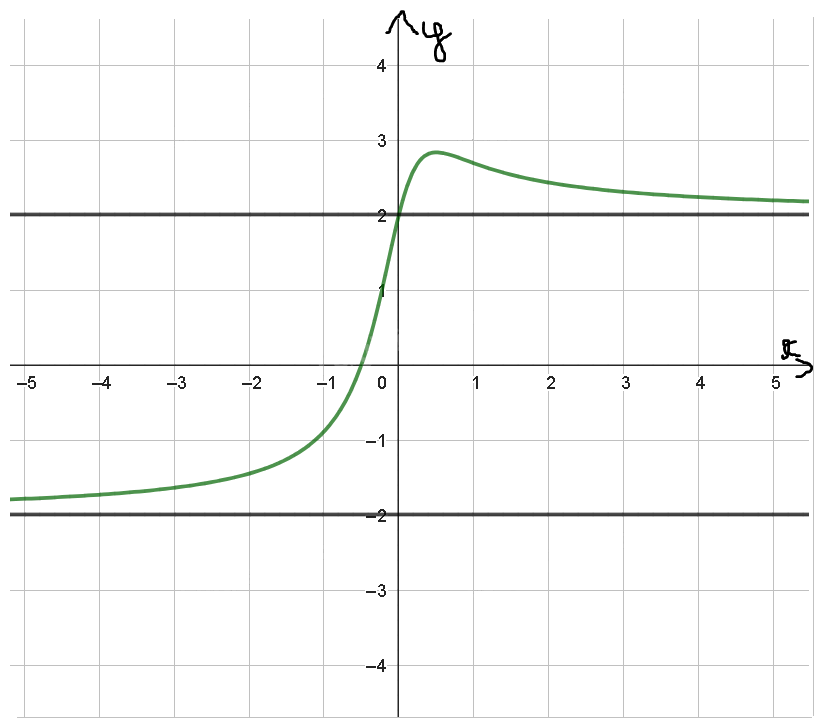
b) Trên trục Oy tại điểm có giá trị bằng 2 vẽ một đường thẳng song song với Ox. Trên trục Oy tại điểm có giá trị bằng -2 vẽ một đường thẳng song song với Ox.
Lời giải chi tiết:
a) Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = 2.
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = - 2.
b)
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị hàm số, đặc biệt là các hàm số bậc hai. Đây là nền tảng quan trọng cho các kiến thức nâng cao hơn trong chương trình học. Việc nắm vững các khái niệm, tính chất và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm đỉnh của parabol, trục đối xứng, và vẽ đồ thị hàm số. Để giải bài tập này, học sinh cần nắm vững công thức tính đỉnh, trục đối xứng và cách xác định chiều mở của parabol.
Bài tập này thường liên quan đến việc giải các bài toán thực tế bằng cách sử dụng hàm số bậc hai. Ví dụ, tìm chiều dài, chiều rộng của một hình chữ nhật có diện tích cho trước, hoặc tìm vận tốc, thời gian của một vật chuyển động. Để giải bài tập này, học sinh cần biết cách lập phương trình hàm số bậc hai dựa trên các điều kiện của bài toán, sau đó giải phương trình để tìm nghiệm.
Các bài tập tổng hợp thường kết hợp nhiều kiến thức và kỹ năng khác nhau. Học sinh cần vận dụng linh hoạt các kiến thức đã học để giải quyết các bài toán phức tạp hơn.
Để giải bài tập Toán 12 tập 1 hiệu quả, học sinh cần:
Toán học là một môn học đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian học tập và luyện tập thường xuyên để đạt được kết quả tốt nhất. Đừng ngại thử thách bản thân và tìm kiếm những phương pháp học tập hiệu quả nhất. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| xđỉnh = -b/2a | Hoành độ đỉnh của parabol |
| yđỉnh = f(xđỉnh) | Tung độ đỉnh của parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |