Chào mừng các em học sinh đến với bài giải bài tập 2.1 trang 54 SGK Toán 12 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.
Cho hình tứ diện đều ABCD (Hình 2.5) a) Có bao nhiêu vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện? Liệt kê tất cả những vectơ đó. b) Bạn Lan nói: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)". Khẳng định của bạn Lan có đúng không? Vì sao?
Đề bài
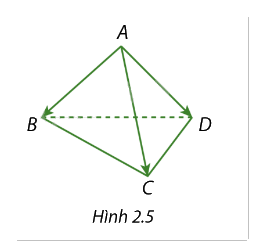
Cho hình tứ diện đều ABCD (Hình 2.5)
a) Có bao nhiêu vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện? Liệt kê tất cả những vectơ đó.
b) Bạn Lan nói: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)". Khẳng định của bạn Lan có đúng không? Vì sao?
Phương pháp giải - Xem chi tiết
- Sử dụng lý thuyết về vectơ để liệt kê các vectơ có điểm đầu và điểm cuối là các đỉnh của hình tứ diện.
- Sử dụng định nghĩa về vectơ bằng nhau để xác định tính đúng sai của khẳng định.
Lời giải chi tiết
a) Số lượng các vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện đều ABCD:
- Một tứ diện đều có 4 đỉnh: A, B, C, D.
- Số vectơ có điểm đầu và điểm cuối là đỉnh của tứ diện đều là số cặp (không lặp lại) trong 4 đỉnh này.
Số lượng các vectơ là:
\(4 \times 3 = 12\)(vì mỗi đỉnh có 3 đỉnh còn lại để tạo vectơ)
Liệt kê các vectơ:
- Từ đỉnh \(A\): \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \)
- Từ đỉnh \(B\): \(\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {BD} \)
- Từ đỉnh \(C\): \(\overrightarrow {CA} ,\overrightarrow {CB} ,\overrightarrow {CD} \)
- Từ đỉnh \(D\): \(\overrightarrow {DA} ,\overrightarrow {DB} ,\overrightarrow {DC} \)
b) Khẳng định của bạn Lan: "\(\overrightarrow {AB} = \overrightarrow {AC} = \overrightarrow {AD} \) vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống dưới)".
Để xét khẳng định này, ta cần kiểm tra:
- Độ dài của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) có bằng nhau không?
- Hướng của các vectơ này có cùng hướng không?
Trong hình tứ diện đều, các cạnh đều có độ dài bằng nhau:
\(|\overrightarrow {AB} | = |\overrightarrow {AC} | = |\overrightarrow {AD} |\)
Tuy nhiên, hướng của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) không cùng phương, vì:
- \(\overrightarrow {AB} \) là vectơ từ \(A\) đến \(B\)
- \(\overrightarrow {AC} \) là vectơ từ \(A\) đến \(C\)
- \(\overrightarrow {AD} \) là vectơ từ \(A\) đến \(D\)
Các vectơ này không song song với nhau mà tạo thành các góc với nhau trong không gian.
Vậy, khẳng định của bạn Lan là sai, vì các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) tuy có cùng độ dài nhưng không cùng phương và cùng hướng.
Bài tập 2.1 trang 54 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Cụ thể, bài tập thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, và tìm cực trị. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức đạo hàm cơ bản, cũng như các phương pháp giải toán liên quan đến đạo hàm.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Đề bài: (Giả sử đề bài cụ thể của bài tập 2.1)
Lời giải:
Để minh họa cho phương pháp giải bài tập này, chúng ta hãy xem xét một ví dụ cụ thể:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.
Lời giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài tập 2.1 trang 54 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về đạo hàm. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và áp dụng thành công vào các bài tập tương tự.