Chào mừng các em học sinh đến với bài giải bài tập 1.7 trang 9 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về hàm số và đồ thị.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Thể tích \(V\) của 1 kg nước (tính bằng cm3¬) ở nhiệt độ \(T\) (đơn vị: oC) khi \(T\) thay đổi từ 0oC đến 30oC được cho xấp xỉ bởi công thức: \(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\) (Nguồn: James Stewart,J(2015).Calculus.Cengage Learning 8th edition, p.284) Tìm nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng( làm tròn kết quả đến hàng đơn vị
Đề bài
Thể tích \(V\) của 1 kg nước (tính bằng cm3) ở nhiệt độ \(T\) (đơn vị: oC) khi \(T\) thay đổi từ 0oC đến 30oC được cho xấp xỉ bởi công thức:
\(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\)
(Nguồn: James Stewart,J(2015).Calculus.Cengage Learning 8th edition, p.284)
Tìm nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng( làm tròn kết quả đến hàng đơn vị
Phương pháp giải - Xem chi tiết
Nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng là tìm khoảng dông biến của hàm số \(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\)
Bước 1: Tính
Bước 2: Lập bảng biến thiên
Bước 3: Xác định khoảng dông biến của hàm số dựa vào bảng biến thiên
Lời giải chi tiết
Ta có: \(V' = - 0,06426 + 2.0,0085043T - 3.0,0000769{T^2}\)
Xét \(V' = 0\)\( \Rightarrow - 0,06426 + 2.0,0085043T - 3.0,0000769{T^2} = 0\)
\( \Rightarrow \left[ \begin{array}{l}T = 69\\T = 4\end{array} \right.\)
Từ đó ta có bảng biến thiên là
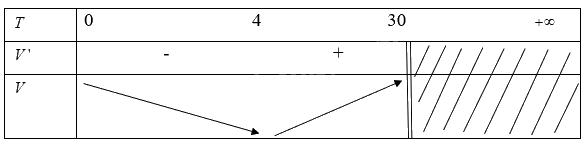
Từ bảng biến thiên ta thấy
Hàm số trên đồng biến từ \({T_0} = 4\)hay thể tích nước tăng từ khi \({T_0} = 4\)
Bài tập 1.7 trang 9 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, đặc biệt là các yếu tố như hệ số a, đỉnh của parabol, trục đối xứng và giao điểm với các trục tọa độ để xác định phương trình hàm số khi biết một số thông tin nhất định.
Bài tập 1.7 thường bao gồm các dạng câu hỏi sau:
Để giải quyết bài tập 1.7 một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Ví dụ: Xác định phương trình parabol (P) có đỉnh I(1; -2) và đi qua điểm A(3; 2).
Giải:
Phương trình parabol có dạng: y = a(x - 1)2 - 2.
Thay tọa độ điểm A(3; 2) vào phương trình, ta có: 2 = a(3 - 1)2 - 2.
=> 2 = 4a - 2 => 4a = 4 => a = 1.
Vậy phương trình parabol (P) là: y = (x - 1)2 - 2 = x2 - 2x - 1.
Để củng cố kiến thức và kỹ năng giải bài tập 1.7, các em có thể tham khảo các bài tập sau:
Bài tập 1.7 trang 9 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc hai và các ứng dụng của nó. Bằng cách nắm vững các phương pháp giải và rèn luyện kỹ năng thường xuyên, các em sẽ tự tin giải quyết các bài tập tương tự trong các kỳ thi sắp tới.