Chào mừng bạn đến với bài học về lý thuyết đường tiệm cận của đồ thị hàm số trong chương trình Toán 12 tại giaitoan.edu.vn. Đây là một phần kiến thức quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia.
Bài học này sẽ cung cấp cho bạn một cái nhìn tổng quan về các loại đường tiệm cận, cách xác định chúng và ứng dụng trong việc vẽ đồ thị hàm số.
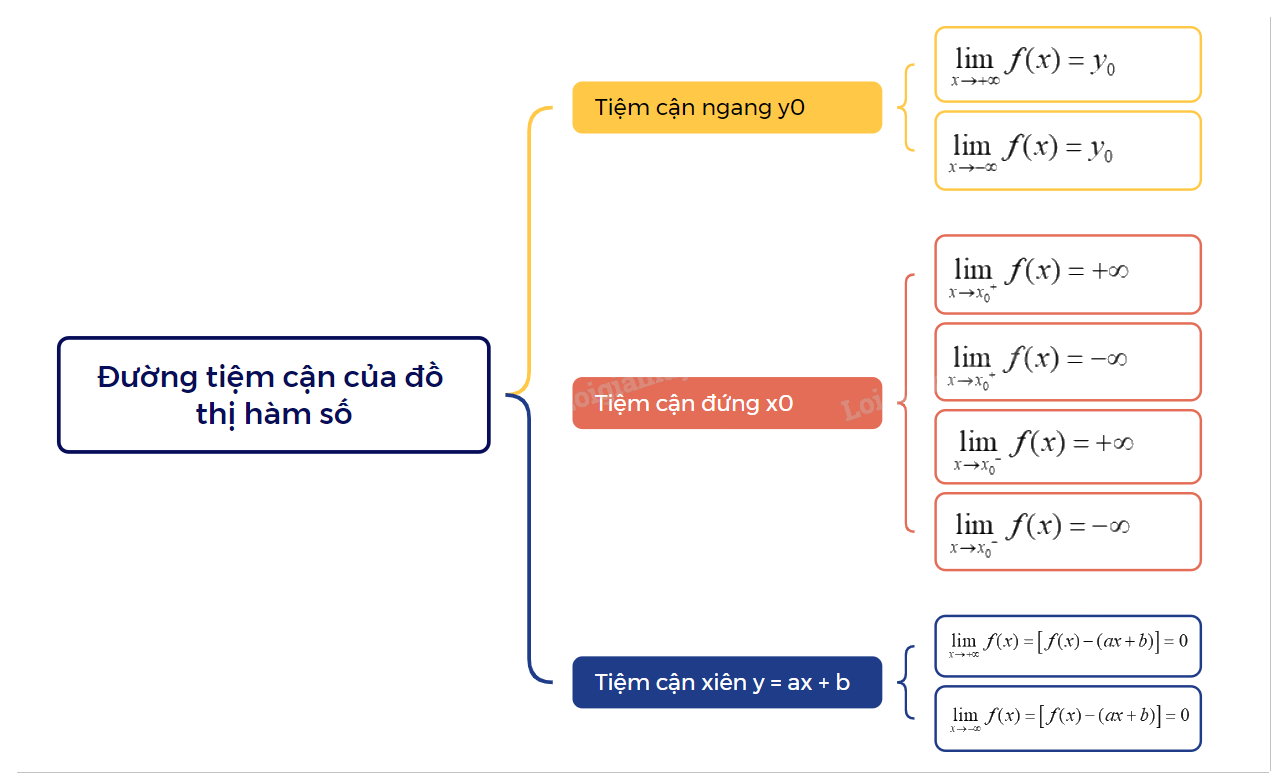
1. Đường tiệm cận ngang của đồ thị hàm số
1. Đường tiệm cận ngang của đồ thị hàm số
| Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\). |
Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\).
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\).
Vậy đồ thị hàm số f(x) có TCN là y = 3.
2. Đường tiệm cận đứng của đồ thị hàm số
| Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \). |
Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\).
Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3x - 2}}{{x + 2}} = + \infty \).
Vậy đồ thị hàm số có TCĐ là x = -2.
3. Đường tiệm cận xiên của đồ thị hàm số
Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\). |
Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\).
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\).
Vậy đồ thị hàm số có TCX là y = x.
Đường tiệm cận là một khái niệm quan trọng trong việc nghiên cứu đồ thị hàm số. Hiểu rõ về đường tiệm cận giúp chúng ta phác thảo chính xác hình dạng của đồ thị và phân tích các tính chất của hàm số.
Đường tiệm cận của đồ thị hàm số y = f(x) là đường thẳng mà đồ thị của hàm số tiếp cận khi x hoặc y tiến tới vô cùng.
Có ba loại đường tiệm cận chính:
Để xác định các đường tiệm cận của đồ thị hàm số, ta thực hiện các bước sau:
Xét hàm số y = (2x + 1) / (x - 1).
Đường tiệm cận có nhiều ứng dụng trong việc:
Hãy tự giải các bài tập sau để củng cố kiến thức về đường tiệm cận:
Lý thuyết đường tiệm cận là một phần kiến thức nền tảng trong chương trình Toán 12. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập sẽ giúp bạn đạt kết quả tốt trong các kỳ thi.
Chúc bạn học tập tốt tại giaitoan.edu.vn!