Chào mừng bạn đến với bài học về Lý thuyết Phương trình đường thẳng trong không gian Toán 12 tại giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng và thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia.
Bài học này sẽ cung cấp cho bạn kiến thức nền tảng vững chắc về phương trình đường thẳng, các dạng phương trình, và cách ứng dụng để giải quyết các bài toán thực tế.
1. Phương trình tham số và phương trình chính tắc của đường thẳng Vecto chỉ phương của đường thẳng
1. Phương trình tham số và phương trình chính tắc của đường thẳng
Vecto chỉ phương của đường thẳng
| Vecto \(\overrightarrow a \ne \overrightarrow 0 \) được gọi là vecto chỉ phương của đường thẳng d nếu giá của \(\overrightarrow a \) song song hoặc trùng với d. |
Ví dụ: Cho hình hộp ABCD.A′B′C′D′, đường thẳng d đi qua hai điểm A và C. Tìm bốn vecto có điểm đầu và điểm cuối trong các đỉnh của hình hộp đã cho và là vecto chỉ phương của d.
Giải:
Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \) có giá trị trùng với d, hai vectơ \(\overrightarrow {A'C'} \) và \(\overrightarrow {C'A'} \) có giá song song với d (do AC//A′C′).
Vậy ta có bốn vectơ chỉ phương của đường thẳng d là \(\overrightarrow {AC} \), \(\overrightarrow {CA} \), \(\overrightarrow {A'C'} \), \(\overrightarrow {C'A'} \).
Phương trình tham số của đường thẳng
Trong không gian Oxyz, cho đường thẳng d đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\). Hệ phương trình: \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) được gọi là phương trình tham số của đường thẳng d (t là tham số, \(t \in R\)). |
Ví dụ: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M(2;−2;1) và có vectơ chỉ phương là \(\overrightarrow a = (1; - 1;2)\).
a) Viết phương trình tham số của đường thẳng d.
b) Trong hai điểm A(3;−3;3) và B(1;−1;1), điểm nào thuộc d?
Giải a) Phương trình tham số của d là \(\left\{ \begin{array}{l}x = 2 + t\\y = - 2 - t\\z = 1 + 2t\end{array} \right.\) \((t \in \mathbb{R})\).
b) Điểm \({M_0}({x_0};{y_0};{z_0})\) thuộc đường thẳng d khi và chỉ khi có giá trị t thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}{x_0} = 2 + t\\{y_0} = - 2 - t\\{z_0} = 1 + 2t\end{array} \right.\).
Ta có:
Với A(3;−3;3), ta xét \(\left\{ \begin{array}{l}3 = 2 + t\\ - 3 = - 2 - t\\3 = 1 + 2t\end{array} \right.\). Hệ phương trình này có nghiệm duy nhất t = 1 nên A thuộc đường thẳng d.
Với B(1;−1;1), ta xét \(\left\{ \begin{array}{l}1 = 2 + t\\ - 1 = - 2 - t\\1 = 1 + 2t\end{array} \right.\). Hệ phương trình này vô nghiệm nên B không thuộc d.
Phương trình chính tắc của đường thẳng
Trong không gian Oxyz, cho đường thẳng d đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\) với \({a_1}\), \({a_2}\), \({a_3}\) đều khác 0. Hệ phương trình \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\) được gọi là phương trình chính tắc của đường thẳng d. |
Ví dụ: Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng d, biết:
a) Đường thẳng d đi qua điểm M(4;2;−1) và có vectơ chỉ phương \(\overrightarrow a = ( - 1; - 4;3)\).
b) Đường thẳng d có phương trình tham số là \(\left\{ \begin{array}{l}x = 2 - t\\y = - 1 + 2t\\z = 3 - 3t\end{array} \right.\) \((t \in \mathbb{R})\).
Giải:
a) Phương trình chính tắc của đường thẳng d là \(\frac{{x - 4}}{{ - 1}} = \frac{{y - 2}}{{ - 4}} = \frac{{z + 1}}{3}\).
b)
Cách 1: Từ phương trình tham số của d, ta có đồ thị qua điểm M(2;−1;3) và có một vectơ chỉ phương \(\overrightarrow a = ( - 1;2; - 3)\).
Suy ra, phương trình chính tắc của d là \(\frac{{x - 2}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z - 3}}{{ - 3}}\).
Cách 2: Từ phương trình tham số của dd, tính theo x , y, z, ta có \(\left\{ \begin{array}{l}t = \frac{{x - 2}}{{ - 1}}\\t = \frac{{y + 1}}{2}\\t = \frac{{z - 3}}{{ - 3}}\end{array} \right.\).
Vậy \(\frac{{x - 2}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z - 3}}{{ - 3}}\). Đây là phương trình chính tắc của d.
Phương trình đường thẳng đi qua hai điểm
Trong không gian Oxyz, cho hai điểm phân biệt \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\). + Đường thẳng AB có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_A} + ({x_B} - {x_A})t\\y = {y_A} + ({y_B} - {y_A})t\\z = {z_A} + ({z_B} - {z_A})t\end{array} \right.\) \((t \in R)\). + Nếu \({x_A} \ne {x_B},{y_A} \ne {y_B},{z_A} \ne {z_B}\) thì đường thẳng AB có phương trình chính tắc là: \(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{z - {z_A}}}{{{z_B} - {z_A}}}\). |
Ví dụ: Trong không gian Oxyz, viết phương trình tham số và phương trình chính tắc của đường thẳng đi qua hai điểm A(4; 2; -1) và B(3; -2; 2).
Giải:
Phương trình tham số của AB là:
\(\left\{ \begin{array}{l}x = 4 + (3 - 4)t\\y = 2 + ( - 2 - 2)t\\z = - 1 + (2 + 1)t\end{array} \right.\) \((t \in R)\) hay \(\left\{ \begin{array}{l}x = 4 - t\\y = 2 - 4t\\z = - 1 + 3t\end{array} \right.\) \((t \in R)\).
Phương trình chính tắc của đường thẳng AB là:
\(\frac{{x - 4}}{{3 - 4}} = \frac{{y - 2}}{{ - 2 - 2}} = \frac{{z - ( - 1)}}{{2 - ( - 1)}}\) hay \(\frac{{x - 4}}{{ - 1}} = \frac{{y - 2}}{{ - 4}} = \frac{{z + 1}}{3}\).
2. Vị trí tương đối giữa hai đường thẳng trong không gian. Điều kiện để hai đường thẳng vuông góc trong không gian
Trong không gian Oxyz, cho hai đường thẳng
d: \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\) và \({M_0}({x_0};{y_0};{z_0}) \in d\);
d’: \(\left\{ \begin{array}{l}x = {x_0}' + {a_1}'t'\\y = {y_0}' + {a_2}'t'\\z = {z_0}' + {a_3}'t'\end{array} \right.\) có vecto chỉ phương \(\overrightarrow {a'} = ({a_1}';{a_2}';{a_3}')\).
Khi đó:
+ d//d’ khi và chỉ khi \(\overrightarrow a \) cùng phương với \(\overrightarrow {a'} \) và \({M_0} \notin d'\). + d trùng d’ khi và chỉ khi \(\overrightarrow a \) cùng phương với \(\overrightarrow {a'} \) và \({M_0} \in d'\). + d cắt d’ khi và chỉ hệ phương trình ẩn t, t’ sau: \(\left\{ \begin{array}{l}{x_0} + {a_1}t = {x_0}' + {a_1}'t'\\{y_0} + {a_2}t = {y_0}' + {a_2}'t'\\{z_0} + {a_3}t = {z_0}' + {a_3}'t'\end{array} \right.\) có đúng một nghiệm. + d và d’ chéo nhau khi và chỉ khi \(\overrightarrow a \) không cùng phương với \(\overrightarrow {a'} \) và hệ: \(\left\{ \begin{array}{l}{x_0} + {a_1}t = {x_0}' + {a_1}'t'\\{y_0} + {a_2}t = {y_0}' + {a_2}'t'\\{z_0} + {a_3}t = {z_0}' + {a_3}'t'\end{array} \right.\) vô nghiệm. |
Lưu ý:
- Khi xét vị trí tương đối của hai đường thẳng, người ta thường xét tính cùng phương của hai vectơ chỉ phương của hai đường thẳng đó:
+ Nếu hai vectơ chỉ phương cùng phương thì hai đường thẳng đó song song hoặc trùng nhau.
+ Nếu hai vectơ chỉ phương không cùng phương thì hai đường thẳng đó cắt nhau hoặc chéo nhau.
- Ta có thể sử dụng tích có hướng và tích vô hướng để xét vị trí tương đối của hai đường thẳng. Chẳng hạn: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M, có vectơ chỉ phương \(\overrightarrow a \) và đường thẳng d′ đi qua điểm M′, có vectơ chỉ phương \(\overrightarrow {a'} \). Khi \(\left[ {\overrightarrow a ,\overrightarrow {a'} } \right] \ne \overrightarrow 0 \):
+ Nếu \(\left[ {\overrightarrow a ,\overrightarrow {a'} } \right].\overrightarrow {MM'} = 0\) thì d và d′ cắt nhau.
+ Nếu \(\left[ {\overrightarrow a ,\overrightarrow {a'} } \right].\overrightarrow {MM'} \ne 0\) thì d và d′ chéo nhau.
Ví dụ: Trong không gian Oxyz, xét vị trí tương đối của các cặp đường thẳng sau:
a) d: \(\left\{ \begin{array}{l}x = 1 + t\\y = 2t\\z = 3 - t\end{array} \right.\) \((t \in R)\) hay d’: \(\left\{ \begin{array}{l}x = 2 + 2t'\\y = 3 + 4t'\\z = 5 - 2t'\end{array} \right.\) \((t' \in R)\).
b) d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 1 + 3t\\z = 5 + t\end{array} \right.\) \((t \in R)\) hay d’: \(\frac{{x - 1}}{3} = \frac{{y + 2}}{2} = \frac{{z + 1}}{2}\).
c) d: \(\frac{x}{1} = \frac{{y - 1}}{{ - 1}} = \frac{z}{2}\) và d’: \(\frac{{x - 1}}{5} = \frac{{y - 2}}{1} = \frac{{z + 2}}{{ - 2}}\).
Giải:
a) Ta có các vectơ chỉ phương của d và d′ lần lượt là \(\overrightarrow a = (1;2; - 1)\) và \(\overrightarrow {a'} = (2;4; - 2)\).
Vì \(\overrightarrow {a'} = 2\overrightarrow a \) nên \(\overrightarrow a \) và \(\overrightarrow {a'} \) cùng phương. Từ đó suy ra d và d′ song song với nhau hoặc trùng nhau.
Xét điểm \(M\left( {1;0;3} \right) \in d\), ta có \(M \notin d'\) nên d//d′.
b) Ta có d và d′ lần lượt nhận \(\overrightarrow a = \left( {2;3;1} \right)\;\) và \(\overrightarrow {a'} = \left( {3;2;2} \right)\;\) là các vectơ chỉ phương.
Vì \(\overrightarrow a \) và \(\overrightarrow {a'} \) không cùng phương nên d và d′ cắt nhau hoặc chéo nhau.
Có d′ đi qua M(1;2;−1) và có vectơ chỉ phương \(\overrightarrow {a'} = \left( {3;2;2} \right)\;\) nên có phương trình tham số là d’: \(\left\{ \begin{array}{l}x = 1 + 3t'\\y = - 2 + 2t'\\z = - 1 + 2t'\end{array} \right.\) \((t' \in R)\).
Xét hệ phương trình: \(\left\{ \begin{array}{l}1 + 2t = 1 + 3t'\\ - 1 + 3t = - 2 + 2t'\\5 + t = - 1 + 2t'\end{array} \right.\) ta không tìm được giá trị t, t’ thỏa mãn cả ba phương trình của hệ. Ta suy ra hệ trên vô nghiệm.
Vậy d và d’ chéo nhau.
c) Ta có: d đi qua M(0;1;0) và có vectơ chỉ phương \(\overrightarrow a = \left( {1; - 1;2} \right)\).
d′ đi qua M′(1;2;−2) và có vectơ chỉ phương \(\overrightarrow {a'} = (5;1; - 2)\).
Nên phương trình tham số của d và d′ lần lượt là:
d: \(\left\{ \begin{array}{l}x = t\\y = 1 - t\\z = 2t\end{array} \right.\) \((t \in R)\) và d’: \(\left\{ \begin{array}{l}x = 1 + 5t'\\y = 2 + t'\\z = - 2 - 2t'\end{array} \right.\) \((t' \in R)\).
Xét hệ phương trình: \(\left\{ \begin{array}{l}t = 1 + 5t'\\1 - t = 2 + t'\\2t = - 2 - 2t'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t - 5t' = 1\\ - t - t' = 2\\2t + 2t' = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - \frac{2}{3}\\t' = - \frac{1}{3}\end{array} \right.\).
Hệ phương trình trên có đúng một nghiệm, nên d và d’ cắt nhau.
Điều kiện để hai đường thẳng vuông góc
Trong không gian Oxyz, cho hai đường thẳng d và d’ tương ứng có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow {a'} = ({a_1}';{a_2}';{a_3}')\). Khi đó: \(d \bot d' \Leftrightarrow \overrightarrow a \cdot \overrightarrow {a'} = 0 \Leftrightarrow {a_1}{a_1}' + {a_2}{a_2}' + {a_3}{a_3}' = 0\). |
Ví dụ: Trong không gian Oxyz, chứng minh hai đường thẳng sau đây vuông góc với nhau:
d': \(\left\{ \begin{array}{l}x = 5 - t\\y = - 3 + 2t\\z = 4t\end{array} \right.\) \((t \in R)\) và d’: \(\frac{{x - 9}}{2} = \frac{{y - 13}}{3} = \frac{{z - 1}}{{ - 1}}\).
Giải:
d và d’ lần lượt có vecto chỉ phương là \(\overrightarrow a = \left( { - 1;2;4} \right)\;\) và \(\overrightarrow {a'} = \left( {2;3; - 1} \right)\;\).
Ta có \(\overrightarrow a .\overrightarrow {a'} = - 2 + 6 - 4 = 0\) Suy ra \(\overrightarrow a \bot \overrightarrow {a'} \). Vậy \(d \bot d'\).
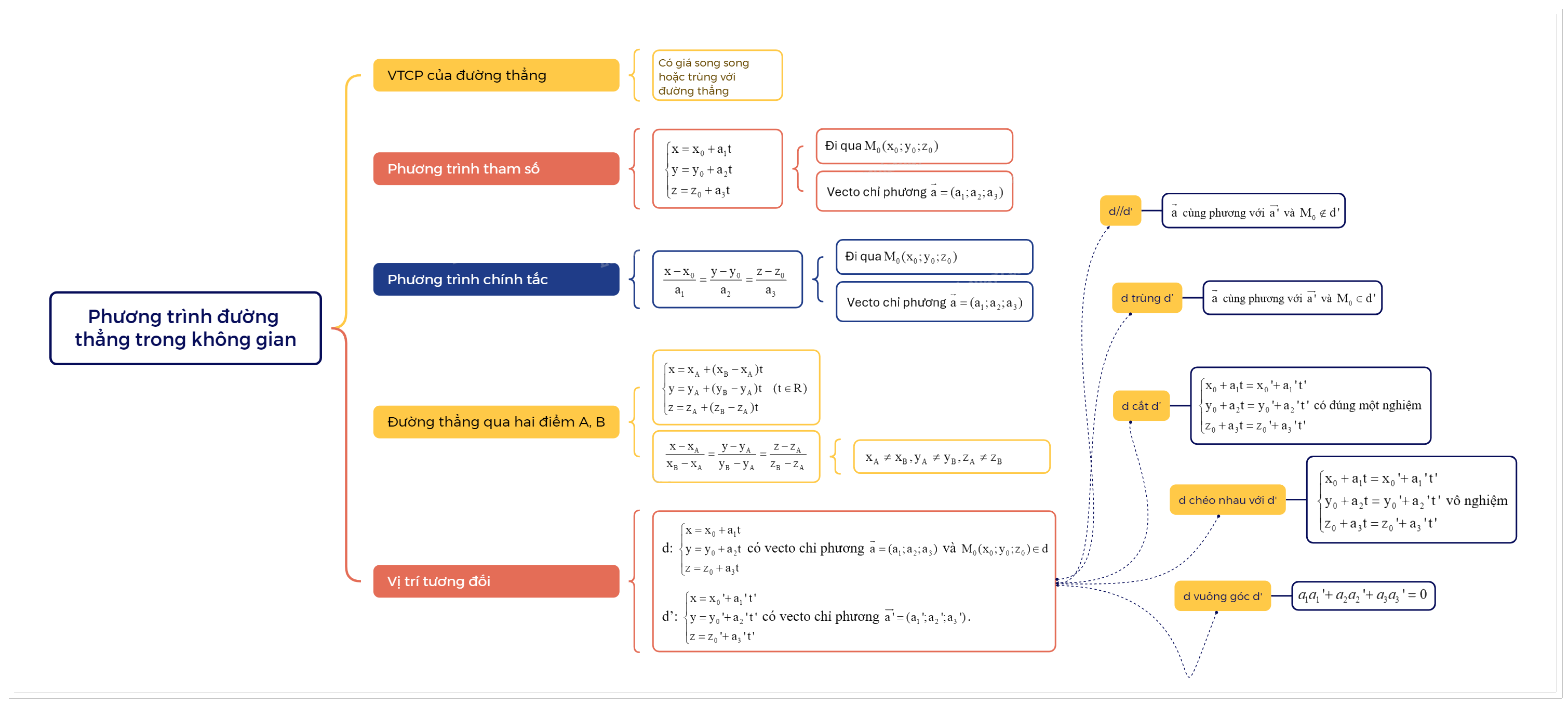
Trong không gian Oxyz, đường thẳng là tập hợp các điểm thỏa mãn một phương trình nhất định. Việc nắm vững lý thuyết về phương trình đường thẳng là vô cùng quan trọng để giải quyết các bài toán hình học không gian một cách hiệu quả.
Có ba dạng phương trình thường gặp của đường thẳng trong không gian:
Vectơ chỉ phương của đường thẳng là một vectơ song song với đường thẳng đó. Nếu đường thẳng đi qua hai điểm A(xA, yA, zA) và B(xB, yB, zB) thì vectơ AB = (xB - xA, yB - yA, zB - zA) là một vectơ chỉ phương của đường thẳng.
Cho hai đường thẳng d1 và d2 có vectơ chỉ phương lần lượt là u1 và u2:
Khoảng cách d từ điểm M(xM, yM, zM) đến đường thẳng Δ có phương trình tham số x = x0 + at, y = y0 + bt, z = z0 + ct được tính theo công thức:
d = |[AM x u]| / |u|, trong đó A là một điểm thuộc đường thẳng Δ, u là vectơ chỉ phương của Δ, và AM là vectơ từ A đến M.
Ví dụ 1: Viết phương trình tham số của đường thẳng đi qua điểm A(1, 2, 3) và có vectơ chỉ phương u = (2, -1, 1).
Giải: Phương trình tham số của đường thẳng là: x = 1 + 2t, y = 2 - t, z = 3 + t.
Ví dụ 2: Tìm góc giữa hai đường thẳng d1 và d2 có vectơ chỉ phương u1 = (1, 0, 0) và u2 = (0, 1, 0).
Giải: Góc θ giữa hai đường thẳng được tính bởi công thức: cos θ = (u1.u2) / (|u1||u2|) = 0. Vậy θ = 90o, hai đường thẳng vuông góc với nhau.
Để nắm vững kiến thức về phương trình đường thẳng trong không gian, bạn nên luyện tập thêm nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú và đa dạng, giúp bạn rèn luyện kỹ năng giải toán một cách hiệu quả.
Chúc bạn học tốt!