Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 1.32 trang 45 SGK Toán 12 tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
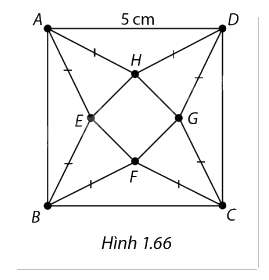
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn Nam làm một hình chóp tứ giác đều S.EFGH bằng cách sử dụng một tấm bìa hình vuông ABCD có cạnh bằng 5 cm và cắt tấm bìa theo các tam giác cân AEB, BFC, CGD, DHA. Sau đó bạn gấp các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành đỉnh S của khối chóp tứ giác đều như hình 1.66. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng bao nhiêu?
Đề bài
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn Nam làm một hình chóp tứ giác đều S.EFGH bằng cách sử dụng một tấm bìa hình vuông ABCD có cạnh bằng 5 cm và cắt tấm bìa theo các tam giác cân AEB, BFC, CGD, DHA. Sau đó bạn gấp các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành đỉnh S của khối chóp tứ giác đều như hình 1.66. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng bao nhiêu?
Phương pháp giải - Xem chi tiết
- Đặt x là độ dài các cạnh của hình vuông EFGH.
- Tính diện tích của hình vuông EFGH theo x.
- Tìm chiều cao từ đỉnh S xuống đáy.
- Tìm hàm thể tích và khảo sát.
Lời giải chi tiết
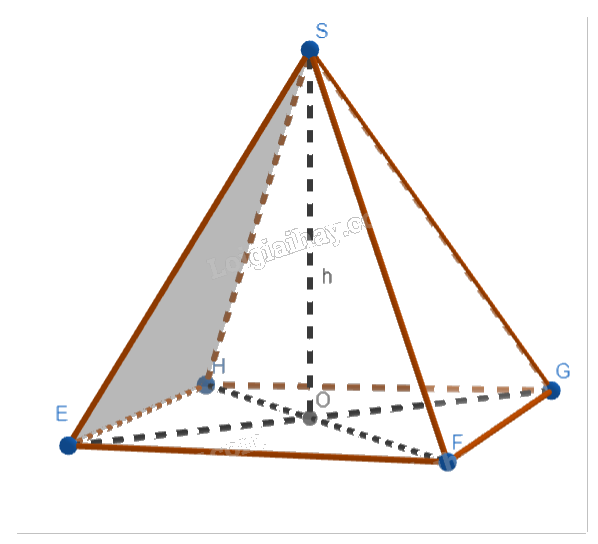
Theo đề bài ta có hình vẽ như sau:
- Đặt x (cm) là độ dài các cạnh của hình vuông EFGH (x∈\((0;2,5\sqrt 2 )\)).
Tương đương EF=FG=GH=EH=x nên \({S_{EFGH}} = {x^2}\)
Đặt SO là chiều cao của hình chóp S.EFGH.
- Độ dài đường chéo của hình vuông EFGH là \(HF = EG = \sqrt {{x^2} + {x^2}} = x\sqrt 2 \)cm.
- Ta có: \(SE = AE = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{5 - x\sqrt 2 }}{2}} \right)}^2}} = \sqrt {2.{{\left( {\frac{5}{2}} \right)}^2} - \frac{{2{x^2}}}{4}} = \frac{1}{2}\sqrt {50 - 2{x^2}} \)
- Vì tam giác vuông SOE vuông tại O nên suy ra:
\(SO = \sqrt {S{E^2} - E{O^2}} = \sqrt {\frac{1}{4}(50 - 2{x^2}) - \frac{{2{x^2}}}{4}} = \frac{1}{2}\sqrt {50 - 4{x^2}} \)
- Thể tích của hình chóp S.EFGH là:
\({V_{S.EFGH}} = \frac{1}{3}.{S_{EFGH}}.SO = \frac{1}{3}.{x^2}.\frac{1}{2}\sqrt {50 - 4{x^2}} = \frac{1}{6}{x^2}\sqrt {50 - 4{x^2}} \)
Để thể tích hình chóp S.EFGH là lớn nhất thì \(f(x) = {x^2}\sqrt {50 - 4{x^2}} \) phải đạt giá trị lớn nhất trong khoảng từ \((0;2,5\sqrt 2 )\).
- Tính đạo hàm: \(f'(x) = 2x\sqrt {50 - 4{x^2}} + {x^2}.\frac{{ - 4x}}{{\sqrt {50 - 4{x^2}} }} = \frac{{ - 12{x^3} + 100x}}{{\sqrt {50 - 4{x^2}} }} = \frac{{4x(3{x^2} - 25)}}{{\sqrt {50 - 4{x^2}} }}\)
- Giải phương trình \(f'(x) = 0\)
\[4x(3{x^2} - 25) = 0 \Leftrightarrow {x_1} = 0,{x_2} = \frac{5}{{\sqrt 3 }},{x_3} = - \frac{5}{{\sqrt 3 }}\](loại \({x_1},{x_3}\) vì x > 0).
- Bảng biến thiên:
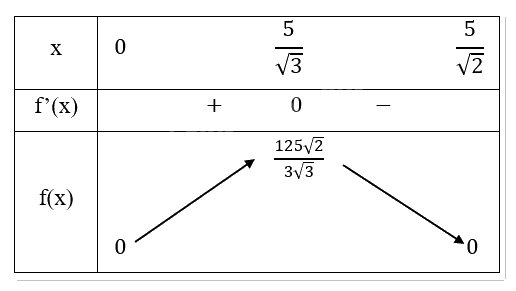
Nhận thấy \(f(x)\) sẽ đạt giá trị lớn nhất tại \(x = \frac{5}{{\sqrt 3 }}\)
Vậy thể tích lớn nhất của khối chóp tứ giác đều tạo thành là \(V = \frac{1}{6}.{\left( {\frac{5}{{\sqrt 3 }}} \right)^2}.\sqrt {50 - 4{{\left( {\frac{5}{{\sqrt 3 }}} \right)}^2}} \approx 5,67c{m^3}\).
Bài tập 1.32 trang 45 SGK Toán 12 tập 1 thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các công thức và quy tắc đạo hàm là yếu tố then chốt để hoàn thành bài tập này một cách chính xác.
Bài tập 1.32 thường có dạng như sau: Cho một hàm số y = f(x). Tính đạo hàm f'(x) tại một điểm x cụ thể hoặc tìm điều kiện để hàm số có đạo hàm tại một điểm. Đôi khi, bài tập còn yêu cầu học sinh sử dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số, hoặc các bài toán tối ưu hóa.
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tính đạo hàm f'(x) và tìm các điểm cực trị của hàm số.
Giải:
Bài tập 1.32 trang 45 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ tự tin hơn trong việc giải quyết bài tập này. Chúc bạn học tập tốt!