Chào mừng bạn đến với bài học về lý thuyết Phương trình mặt cầu trong chương trình Toán 12. Đây là một phần quan trọng của chương trình Hình học không gian, đòi hỏi sự hiểu biết sâu sắc về các khái niệm và công thức liên quan.
Tại giaitoan.edu.vn, chúng tôi cung cấp một lộ trình học tập bài bản, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán liên quan đến phương trình mặt cầu.
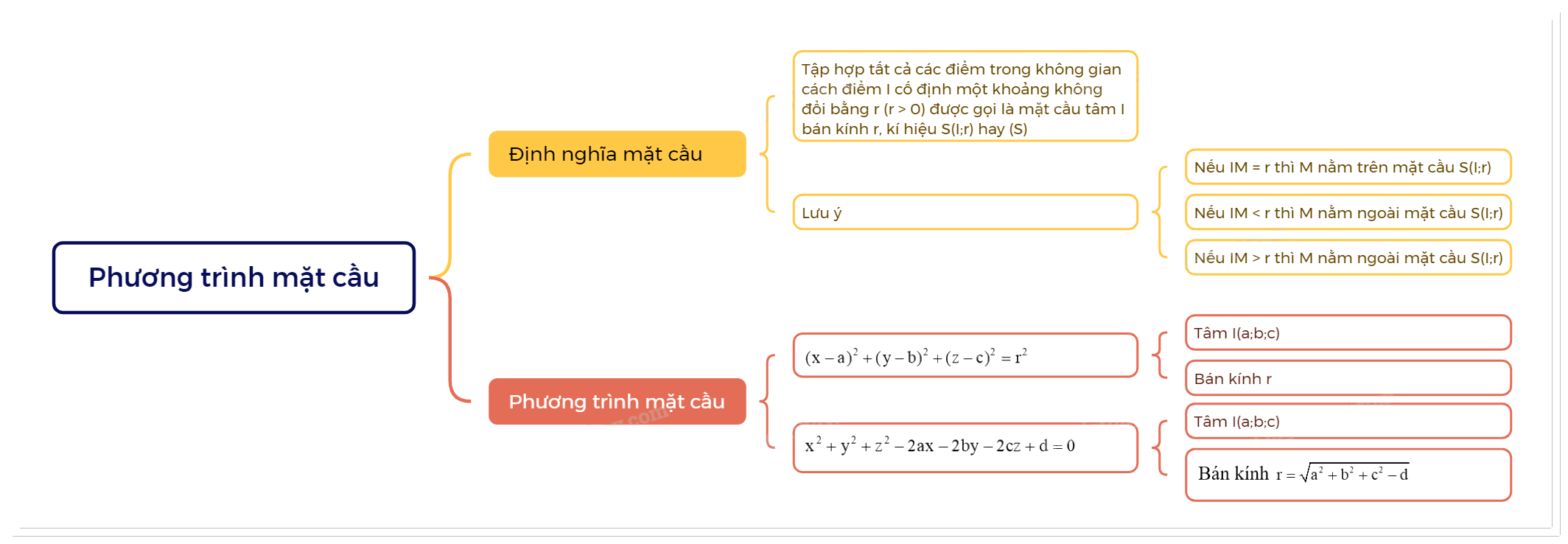
1. Định nghĩa mặt cầu
1. Định nghĩa mặt cầu
| Tập hợp tất cả các điểm trong không gian cách điểm I cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm I bán kính r, kí hiệu S(I;r) hay (S). |
Lưu ý: Cho mặt cầu S(I;r) và điểm M bất kì trong không gian.
- Nếu IM = r thì M nằm trên mặt cầu S(I;r).
- Nếu IM < r thì M nằm ngoài mặt cầu S(I;r).
- Nếu IM > r thì M nằm ngoài mặt cầu S(I;r).
Ví dụ:
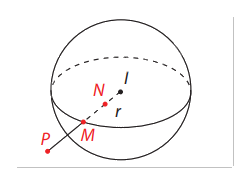
- Điểm M nằm trên mặt cầu (S). - Điểm N nằm trong mặt cầu (S). - Điểm P nằm ngoài mặt cầu (S).
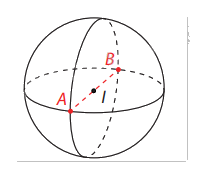
- Nếu hai điểm A, B nằm trên mặt cầu S(I;r) và đoạn thẳng AB đi qua tâm I thì AB được gọi là một đường kính của mặt cầu. Khi đó độ dài đường kính bằng 2r. - Một mặt cầu được xác định khi ta biết tâm và bán kính hoặc biết một đường kính của nó.
Ví dụ: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu tâm I(-2;1;5) bán kính 3. Các điểm A(10;1;2), B(0;1;4), C(0;3;4) nằm trong, nằm trên hay nằm ngoài mặt cầu đó?
Giải:
Do \(IA = \sqrt {{{\left( {10 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}} = \sqrt {153} > 3\) nên điểm A(10;1;2) nằm ngoài mặt cầu đó.
Do \(IB = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 5 < 3\) nên điểm B(0;1;4) nằm trong mặt cầu đó.
Do \(IC = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {3 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 9 = 3\) nên điểm C(0;3;4) nằm trên mặt cầu đó.
2. Phương trình mặt cầu
Phương trình của mặt cầu tâm I(a;b;c) bán kính r là \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}\). |
Ví dụ 1: Trong không gian Oxyz, xác định tâm I và bán kính r của mặt cầu có phương trình:
a) \({(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 16\).
b) \({(x + 2)^2} + {y^2} + {(z + 3)^2} = 4\).
Giải:
a) Ta có \({(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 16 \Leftrightarrow {(x - 1)^2} + {(y - ( - 2))^2} + {(z - 3)^2} = {4^2}\).
Vậy đây là phương trình mặt cầu có tâm I(1;-2;3) và bán kính r = 4.
b) Ta có \({(x + 2)^2} + {y^2} + {(z + 3)^2} = 4 \Leftrightarrow {(x - ( - 2))^2} + {(y - 0)^2} + {(z - ( - 3))^2} = {2^2}\).
Vậy đây là phương trình mặt cầu có tâm I(-2;0;-3) và bán kính r = 2.
Ví dụ 2: Viết phương trình mặt cầu, biết:
a) Có tâm I(1;2;3), bán kính R = 10.
b) Có tâm I(3;-1;-5) và đi qua điểm B(0;2;1).
Giải:
a) Phương trình của mặt cầu tâm I(1;2;3) bán kính R = 10 là \({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 100\).
b) Bán kính mặt cầu là \(R = IB = \sqrt {{{(0 - 3)}^2} + {{(2 + 1)}^2} + {{(1 + 5)}^2}} = \sqrt {54} \).
Phương trình mặt cầu tâm I(3;-1;-5) bán kính \(R = \sqrt {54} \) là \({(x - 3)^2} + {(y + 1)^2} + {(z + 5)^3} = 54\).
Nhận xét:
Cho mặt cầu tâm I(a;b;c) bán kính r có phương trình \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}\). Ta có thể viết phương trình đó dưới dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\), với \(d = {a^2} + {b^2} + {c^2} - {R^2}\).
Dạng phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) xác định một mặt cầu khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\) với tâm I(a;b;c) và bán kính \(r = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Ví dụ 3: Mỗi phương tình sau có là phương trình mặt cầu hay không? Vì sao?
a) \(2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0\).
b) \({x^2} + {y^2} - 2x + 6y - 8z - 3 = 0\).
Giải:
a) Phương trình \(2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0\) không phải phương trình mặt cầu vì hệ số của \({x^2}\) và \({y^2}\) khác nhau.
b) Phương trình \({x^2} + {y^2} - 2x + 6y - 8z - 3 = 0\) không phải phương trình mặt cầu vì không có biểu thức \({z^2}\).
Ví dụ 4: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0\).
b) \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0\).
Giải:
a) Phương trình \({x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = 2;b = - 5;c = 1;d = 14\).
Ta có \({a^2} + {b^2} + {c^2} - d = 4 + 25 + 1 - 14 = 16 > 0\).
Suy ra phương trình đã cho là phương trình mặt cầu tâm I(2;-5;1), bán kính R = 4.
b) Phương trình \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - 1;b = - 2;c = 3;d = 20\).
Ta có \({a^2} + {b^2} + {c^2} - d = 1 + 4 + 9 - 20 = - 6 < 0\).
Suy ra phương trình đã cho không phải phương trình mặt cầu.
Phương trình mặt cầu là một trong những chủ đề quan trọng trong chương trình Hình học không gian lớp 12. Hiểu rõ lý thuyết và phương pháp giải các bài toán liên quan là yếu tố then chốt để đạt kết quả cao trong các kỳ thi.
Mặt cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính). Công thức tổng quát của mặt cầu có tâm I(a, b, c) và bán kính R là:
(x - a)² + (y - b)² + (z - c)² = R²
Trong đó:
Phương trình chính tắc của mặt cầu có tâm tại gốc tọa độ O(0, 0, 0) và bán kính R là:
x² + y² + z² = R²
Phương trình tham số của mặt cầu có tâm I(a, b, c) và bán kính R có thể được biểu diễn như sau:
x = a + Rsinφcosθ
y = b + Rsinφsinθ
z = c + Rcosφ
Với 0 ≤ φ ≤ π và 0 ≤ θ ≤ 2π
Phương trình x² + y² + z² + 2Ax + 2By + 2Cz + D = 0 là phương trình của một mặt cầu khi và chỉ khi:
A² + B² + C² - D > 0
Khi đó, tâm của mặt cầu là I(-A, -B, -C) và bán kính là R = √(A² + B² + C² - D)
Lý thuyết phương trình mặt cầu có ứng dụng rộng rãi trong nhiều lĩnh vực như:
Ví dụ 1: Tìm tâm và bán kính của mặt cầu có phương trình: x² + y² + z² - 2x + 4y - 6z + 5 = 0
Giải: Ta có A = -1, B = 2, C = -3, D = 5. Kiểm tra điều kiện: (-1)² + 2² + (-3)² - 5 = 1 + 4 + 9 - 5 = 9 > 0. Vậy đây là phương trình của một mặt cầu. Tâm của mặt cầu là I(1, -2, 3) và bán kính là R = √(9) = 3.
Ví dụ 2: Viết phương trình mặt cầu có tâm I(2, -1, 0) và bán kính R = 5.
Giải: Phương trình mặt cầu là: (x - 2)² + (y + 1)² + z² = 25.
Nắm vững lý thuyết Phương trình mặt cầu Toán 12 là bước quan trọng để bạn có thể giải quyết các bài toán một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để đạt được kết quả tốt nhất. Chúc bạn học tập thành công!