Chào mừng các em học sinh đến với bài giải chi tiết bài tập 2.25 trang 82 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến kiến thức đã học.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin hơn trong quá trình học tập.
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ O, các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz và AB = 1, AD = 2, AA’ = 3. a) Tìm tọa độ các đỉnh của hình hộp. b) Tìm điểm E trên đường thẳng DD’ sao cho \(B'E \bot A'C'\).
Đề bài
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ O, các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz và AB = 1, AD = 2, AA’ = 3.
a) Tìm tọa độ các đỉnh của hình hộp.
b) Tìm điểm E trên đường thẳng DD’ sao cho \(B'E \bot A'C'\).
Phương pháp giải - Xem chi tiết
a) Sử dụng thông tin về các cạnh của hình hộp để xác định tọa độ của các đỉnh.
b) Tìm vectơ chỉ phương của đường thẳng DD’ và B’E. Sử dụng điều kiện \(B'E \bot A'C'\) để thiết lập phương trình và giải tìm tọa độ của E.
Lời giải chi tiết
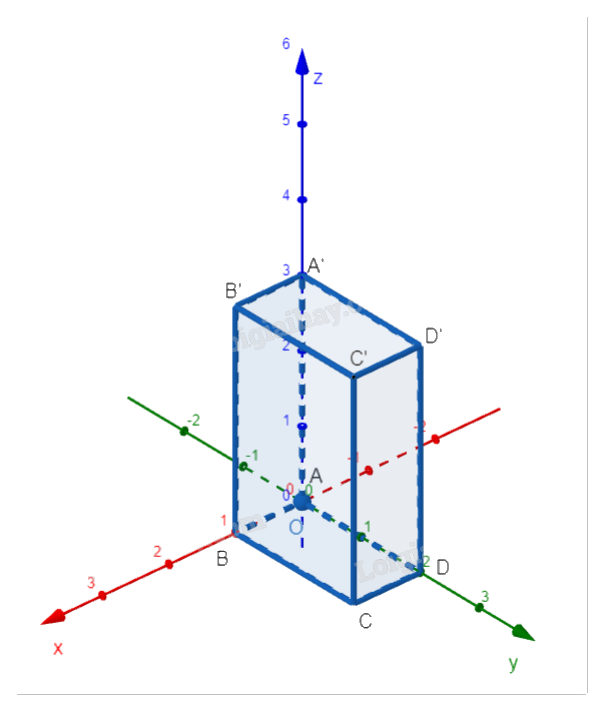
a) Tọa độ các đỉnh của hình hộp chữ nhật là:
- A trùng với gốc tọa độ, tức A(0; 0; 0) .
- B thuộc tia Ox , nên B(1; 0; 0) (vì AB = 1 ).
- D thuộc tia Oy , nên D(0; 2; 0) (vì AD = 2 ).
- A’ thuộc tia Oz , nên A’(0; 0; 3) (vì AA’ = 3 ).
Các đỉnh còn lại của hình hộp chữ nhật:
- C đối với A qua BD , tọa độ là C(1; 2; 0) .
- B’ đối với A qua A’C , tọa độ là B’(1; 0; 3) .
- D’ đối với A qua A’D , tọa độ là D’(0; 2; 3) .
- C’ đối với A qua B’D , tọa độ là C’(1; 2; 3) .
b) Tọa độ của điểm E trên đường thẳng DD’ :
- Đường thẳng DD’ có phương trình dạng:
\(x = 0,\quad y = 2,\quad z = t{\rm{.}}\) với t là tham số.
Tọa độ của E là E(0; 2; t) . Để \(B'E \bot A'C\), cần:
\(\overrightarrow {B'E} \cdot \overrightarrow {A'C} = 0\)
Tính các vectơ:
\(\overrightarrow {B'E} = (0 - 1;2 - 0;t - 3) = ( - 1;2;t - 3)\)
\(\overrightarrow {A'C} = (1 - 0;2 - 0;0 - 3) = (1;2; - 3)\)
Điều kiện vuông góc:
\(\overrightarrow {BE} \cdot \overrightarrow {A'C} = ( - 1) \times 1 + 2 \times 2 + (t - 3) \times ( - 3) = - 1 + 4 - 3t + 9 = 0\)
Giải phương trình này:
\( - 1 + 4 - 3t + 9 = 0\quad \Rightarrow \quad 12 = 3t\quad \Rightarrow \quad t = 4\)
Vậy tọa độ của E là E(0; 2; 4) .
Bài tập 2.25 trang 82 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và định lý đã được học. Để giải bài tập này một cách hiệu quả, chúng ta cần tiếp cận theo các bước sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau đi qua lời giải chi tiết:
(Ở đây sẽ là lời giải chi tiết của bài tập 2.25, bao gồm các bước giải, giải thích và kết luận. Ví dụ, nếu bài toán là về đạo hàm, sẽ trình bày cách tính đạo hàm, phân tích hàm số, tìm cực trị, v.v. Nếu bài toán là về tích phân, sẽ trình bày cách tính tích phân, ứng dụng của tích phân, v.v.)
Ngoài bài tập 2.25, còn rất nhiều bài tập tương tự trong chương trình Toán 12 tập 1. Để giải các bài tập này, các em có thể áp dụng các phương pháp sau:
Kiến thức được sử dụng trong bài tập 2.25 có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như:
Để nắm vững kiến thức và kỹ năng giải bài tập Toán 12 tập 1, các em nên luyện tập thêm các bài tập tương tự. Các em có thể tìm thấy các bài tập này trong SGK, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Bài tập 2.25 trang 82 SGK Toán 12 tập 1 là một bài toán quan trọng, đòi hỏi học sinh phải nắm vững kiến thức và kỹ năng giải bài tập. Hy vọng rằng với lời giải chi tiết và các phương pháp giải đã trình bày, các em sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.
| Khái niệm | Định nghĩa |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của hàm số tại một điểm. |
| Tích phân | Diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành. |
| Bảng tóm tắt các khái niệm quan trọng. | |