Chào mừng bạn đến với bài học về lý thuyết các phép toán vecto trong không gian, một phần kiến thức quan trọng trong chương trình Toán 12. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các công thức cần thiết để giải quyết các bài toán liên quan đến vecto trong không gian.
Chúng ta sẽ cùng nhau khám phá các khái niệm cơ bản, các phép toán như cộng, trừ, nhân với một số thực, tích vô hướng, tích có hướng và ứng dụng của chúng trong hình học không gian.
1. Tổng và hiệu của hai vecto trong không gian a) Tổng của hai vecto
1. Tổng và hiệu của hai vecto trong không gian
a) Tổng của hai vecto
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \). Phép lấy tổng của hai vecto được gọi là phép cộng vecto. - Với 3 điểm A, B, C trong không gian, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (Quy tắc 3 điểm). - Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (Quy tắc hình bình hành). - Nếu ABCD.A’B’C’D’ là hình hộp thì \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (Quy tắc hình hộp). |
b) Hiệu của hai vecto
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là tổng của hai vecto \(\mathop a\limits^ \to \) và vecto đối của \(\mathop b\limits^ \to \), kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \). Phép lấy hiệu của hai vecto được gọi là phép trừ vecto. Với ba điểm O, A, B trong không gian, ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (Quy tắc hiệu). |
2. Tích của một số với một vecto trong không gian
Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: - Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0. - Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\). Phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto. |
3. Tích vô hướng của hai vecto trong không gian
a) Góc giữa hai vecto trong không gian
| Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\). |
b) Tích vô hướng của hai vecto trong không gian
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). |
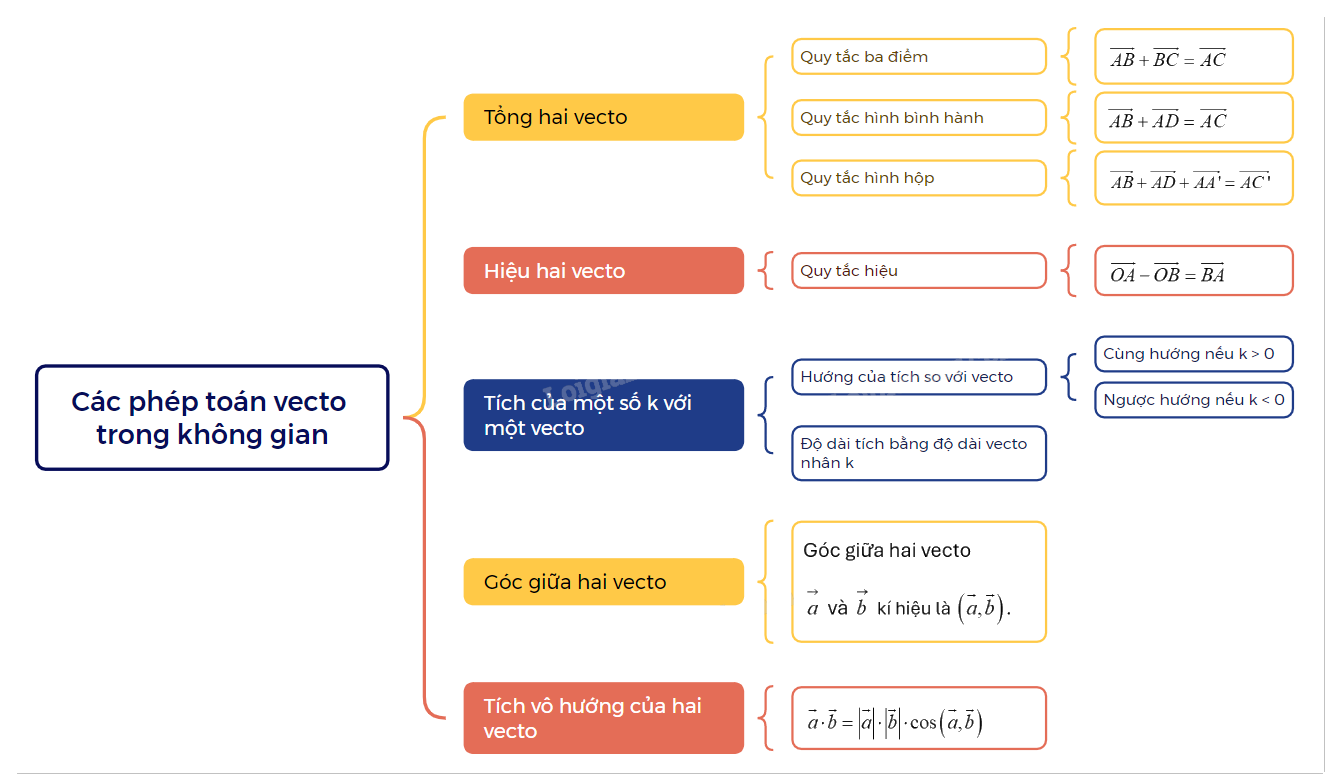
Trong chương trình Toán 12, phần hình học không gian đóng vai trò quan trọng, và vecto trong không gian là công cụ then chốt để giải quyết các bài toán liên quan. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết các phép toán vecto trong không gian, giúp bạn nắm vững kiến thức và tự tin ứng dụng vào giải bài tập.
Một vectơ trong không gian Oxyz được xác định bởi tọa độ (x; y; z). Vectơ a = (x; y; z) có điểm đầu là A(xA; yA; zA) và điểm cuối là B(xB; yB; zB) thì x = xB - xA, y = yB - yA, z = zB - zA.
Độ dài của vectơ a được tính bằng công thức: |a| = √(x2 + y2 + z2).
Tích vô hướng của hai vectơ a = (x1; y1; z1) và b = (x2; y2; z2) được ký hiệu là a.b và được tính bằng công thức:
a.b = x1x2 + y1y2 + z1z2.
Ý nghĩa hình học:a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ a và b.
Ứng dụng:
Tích có hướng của hai vectơ a = (x1; y1; z1) và b = (x2; y2; z2) được ký hiệu là [a, b] và được tính bằng công thức:
[a, b] = (y1z2 - z1y2; z1x2 - x1z2; x1y2 - y1x2).
Ý nghĩa hình học: Vectơ [a, b] vuông góc với cả hai vectơ a và b, và độ dài của nó bằng diện tích hình bình hành tạo bởi hai vectơ a và b.
Ứng dụng:
Ví dụ 1: Cho a = (1; 2; 3) và b = (-2; 1; 0). Tính a.b và [a, b].
Giải:
a.b = (1)(-2) + (2)(1) + (3)(0) = -2 + 2 + 0 = 0.
[a, b] = (2(0) - 3(1); 3(-2) - 1(0); 1(1) - 2(-2)) = (-3; -6; 5).
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết các phép toán vecto trong không gian Toán 12. Chúc bạn học tập tốt!