Chào mừng bạn đến với bài học về Lý thuyết Xác suất có điều kiện Toán 12 trên giaitoan.edu.vn. Đây là một phần kiến thức quan trọng, thường xuyên xuất hiện trong các đề thi THPT Quốc gia và các kỳ thi chuyên ngành. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất, cùng với các ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức một cách hiệu quả.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại.
Xác suất có điều kiện
Xác suất có điều kiện
Cho hai biến cố A và B. Xác suất của biến cố A khi biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B và kí hiệu là P(A|B). Cho hai biến cố A và B bất kì, với P(B) > 0. Khi đó: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\) |
Ví dụ 1: Một hộp có 5 viên bi cùng kích thước và khối lượng, trong đó có 3 viên bi màu đỏ và 2 viên bi màu xanh. Lấy ngẫu nhiên lần lượt 2 viên bi và không hoàn lại. Tính xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ.
Giải:
GọiA là biến cố "Lấy được viên bi thứ hai có màu xanh";
B là biến cố "Lấy được viên bi thứ nhất có màu đỏ".
Khi đột xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ chính là xác suất của A với điều kiện B.
Vì một viên bi đỏ đã được lấy ra ở lần thứ nhất nên trong hợp còn lại 4 viên bi, trong đó có 2 viên bi xanh.
Từ đó ta có: \(P(A\mid B) = \frac{2}{4} = 0,5\).
Vậy xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ là 0,5.
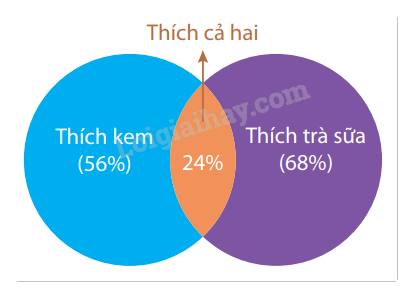
Ví dụ 2: Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có 56% số học sinh thích kem, 68% số học sinh thích trà sữa, 24% số học sinh thích cả trà sữa và kem. Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Tính xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa.
Giải:
Gọi: A là biến cố "Chọn được học sinh thích kem";
B là biến cố "Chọn được học sinh thích trà sữa".
Khi đó xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa chính là xác suất của A với điều kiện B.
Vì có 68% số học sinh thích trà sữa trong nhóm khảo sát nên P(B) = 68% = 0,68.
Ta có AB là biến cố "Chọn được học sinh thích cả trà sữa và kem".
Vì có 24% số học sinh thích cả trà sữa và kem nên P(AB) = 24% = 0,24.
Vì thế ta có: \(P(A\mid B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,24}}{{0,68}} = 0,35\).
Vậy xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa là 0,35.
Công thức nhân xác suất
Với hai biến cố A và B bất kì, ta có: \(P(AB) = P(B).P(A|B) = P(A).P(B|A)\) |
Ví dụ 3: Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T, xác suất để một ngày có gió là 0,6; nếu ngày có gió thì xác suất có mưa là 0,4; nếu ngày không có gió thì xác suất có mưa là 0,2. Gọi G là biến cố "Ngày có gió" và M là biến cố "Ngày có mưa".
a) Vẽ lại sơ đồ hình cây sau và điền vào ô ? các giá trị xác suất tương ứng:
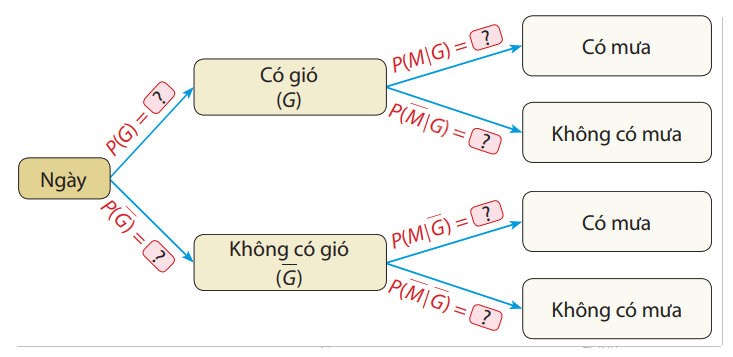
b) Tính xác suất P(GM) và \(P(G\overline M )\). Nêu ý nghĩa của các xác suất này.
Giải:
Theo đề bài, nếu ngày có gió thì xác suất có mưa là 0,4 nên \(P(M\mid G) = 0,4\). Suy ra: \(P(\overline M \mid G) = 1 - 0,4 = 0,6\).
Ngày không có gió thì xác suất có mưa là 0,2 nên \(P(M\mid \overline G ) = 0,2\).
Suy ra: \(P(\overline M \mid \overline G ) = 1 - 0,2 = 0,8\).
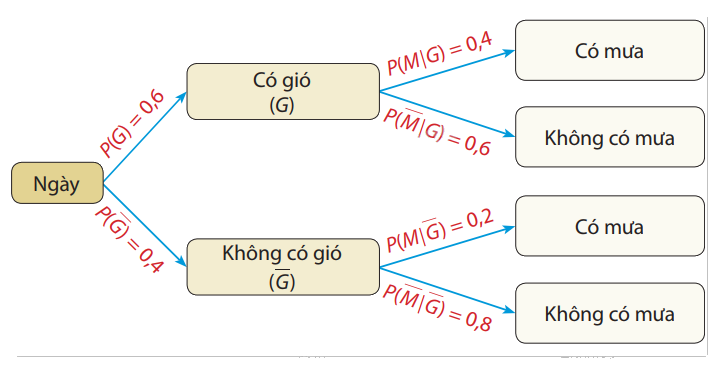
b) \(P(M\mid G) = P\left( G \right).P(M\mid G) = 0,6.0,4 = 0,24.\)
\(P(M\mid \overline G ) = P\left( G \right) \cdot P(M\mid G) = 0,6 \cdot 0,6 = 0,36.\)
Điều này có nghĩa là tại địa phương T, trong một ngày, xác suất để trời vừa có gió và vừa có mưa là 0,24; xác suất để trời có gió nhưng không có mưa là 0,36.
Nhận xét: Xác suất ở mỗi nhánh kể từ đỉnh thứ hai của sơ đồ hình cây là xác suất có điều kiện.

Xác suất có điều kiện là một khái niệm quan trọng trong lý thuyết xác suất, cho phép chúng ta tính toán xác suất của một sự kiện khi biết rằng một sự kiện khác đã xảy ra. Nó là công cụ thiết yếu để phân tích các tình huống phức tạp, nơi kết quả của một sự kiện ảnh hưởng đến khả năng xảy ra của các sự kiện khác.
Giả sử A và B là hai biến cố. Xác suất của biến cố A khi biết biến cố B đã xảy ra, ký hiệu là P(A|B), được gọi là xác suất có điều kiện của A khi biết B. Công thức tính xác suất có điều kiện là:
P(A|B) = P(A ∩ B) / P(B), với P(B) > 0
Trong đó:
Từ công thức xác suất có điều kiện, ta có thể suy ra công thức nhân xác suất:
P(A ∩ B) = P(A|B) * P(B) = P(B|A) * P(A)
Công thức này rất hữu ích trong việc tính xác suất của giao của hai biến cố.
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia. Điều kiện để A và B độc lập là:
P(A|B) = P(A) hoặc P(B|A) = P(B) hoặc P(A ∩ B) = P(A) * P(B)
Ví dụ 1: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng. Tính xác suất để cả hai quả bóng đều màu đỏ.
Giải:
Gọi A là biến cố “cả hai quả bóng đều màu đỏ”.
P(A) = (Số cách chọn 2 quả bóng đỏ) / (Số cách chọn 2 quả bóng bất kỳ)
P(A) = C(5,2) / C(8,2) = 10 / 28 = 5/14
Ví dụ 2: Gieo hai con xúc xắc. Tính xác suất để tổng số chấm trên hai con xúc xắc bằng 7.
Giải:
Gọi B là biến cố “tổng số chấm trên hai con xúc xắc bằng 7”.
Các kết quả có thể xảy ra để tổng bằng 7 là: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1). Có tổng cộng 6 kết quả.
Tổng số kết quả có thể xảy ra khi gieo hai con xúc xắc là 6 * 6 = 36.
P(B) = 6 / 36 = 1/6
Lý thuyết Xác suất có điều kiện Toán 12 là một công cụ mạnh mẽ để giải quyết các bài toán xác suất phức tạp. Việc nắm vững các định nghĩa, tính chất và công thức liên quan sẽ giúp bạn tự tin hơn trong các kỳ thi và ứng dụng thực tế. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.