Chào mừng các em học sinh đến với bài giải bài tập 5.42 trang 85 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
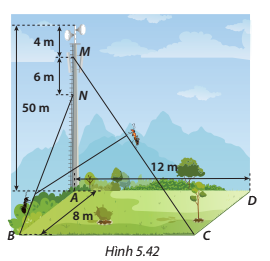
Một tháp phát sóng cao 50 m đặt ở góc A của sân hình chữ nhật ABCD. Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp CM và BN (từ C và B) với vận tốc lần lượt là 3 m/phút và 2,5 m/phút. Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Đề bài
Một tháp phát sóng cao 50 m đặt ở góc A của sân hình chữ nhật ABCD. Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp CM và BN (từ C và B) với vận tốc lần lượt là 3 m/phút và 2,5 m/phút. Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
- Xác định các điểm mà các chú kiến bắt đầu leo lên dây và điểm đến trên cột.
- Tính chiều dài của các đoạn dây (ví dụ: CM và BN) dựa trên vị trí các điểm gốc của dây.
- Dựa vào vận tốc của mỗi chú kiến, tính toán quãng đường mà mỗi chú kiến leo được sau thời gian đã cho.
- Sử dụng tọa độ của hai chú kiến sau thời gian leo lên để xác định khoảng cách giữa chúng, có thể sử dụng công thức khoảng cách giữa hai điểm trong không gian.
Lời giải chi tiết
* Đặt gốc toạ độ tại A, trục Ox chứa cạnh AB, trục Oy chứa cạnh AD và trục Oz chứa cạnh AM
- Toạ độ các điểm là: \(A(0;0;0)\), \(B(8;0;0)\), \(D(0;12;0)\), \(C(8;12;0)\), \(M(0;0;46)\), \(N(0;0;40)\).
* Tính chiều dài của dây cáp CM và BN:
- Dây cáp \(\overrightarrow {CM} ( - 8; - 12;46)\): \(CM = \sqrt {{{(0 - 8)}^2} + {{(0 - 12)}^2} + {{(46 - 0)}^2}} = 2\sqrt {581} \approx 48,2{\mkern 1mu} {\rm{m}}\)
- Dây cáp \(\overrightarrow {BN} ( - 8;0;40)\): \(BN = \sqrt {{{(0 - 8)}^2} + {{(40 - 0)}^2}} = 8\sqrt {26} \approx 40,8{\mkern 1mu} {\rm{m}}\)
* Tính quãng đường hai chú kiến leo lên sau 10 phút:
- Quãng đường chú kiến vàng leo lên dây CM: \({S_{CM}} = 3 \times 10 = 30{\mkern 1mu} {\rm{m}}\)
- Quãng đường chú kiến đen leo lên dây BN: \({S_{BN}} = 2.5 \times 10 = 25{\mkern 1mu} {\rm{m}}\)
* Xác định vị trí của hai chú kiến trên các dây cáp CM và BN sau 10 phút:
- Tỉ lệ vị trí của chú kiến vàng trên dây CM: \(\frac{{{S_{CM}}}}{{CM}} = \frac{{30}}{{48,2}} \approx 0,62\)
- Tọa độ của chú kiến vàng sau 10 phút là:
\(({x_{M'}},{y_{M'}},{z_{M'}}) = 0.62 \times \overrightarrow {CM} + C = (0,62 \times ( - 8);0,62 \times ( - 12);0,62 \times 46) + (8;12;0) \approx (3,04;4,56;28,52)\)
- Tỉ lệ vị trí của chú kiến đen trên dây BN: \(\frac{{{S_{BN}}}}{{BN}} = \frac{{25}}{{40,8}} \approx 0,61\)
- Tọa độ của chú kiến đen sau 10 phút là:
\(({x_{N'}},{y_{N'}},{z_{N'}}) = 0,61 \times \overrightarrow {BN} + \overrightarrow B = (0,61 \times ( - 8);0;0,61 \times 40) + (8;0;0) \approx (3,12;0;24,4)\)
* Tính khoảng cách giữa hai chú kiến Khoảng cách giữa hai chú kiến là:
\(d = \sqrt {{{({x_{M'}} - {x_{N'}})}^2} + {{({y_{M'}} - {y_{N'}})}^2} + {{({z_{M'}} - {z_{N'}})}^2}} \)
Thay các giá trị vào:
\(d = \sqrt {{{(3,04 - 3,12)}^2} + {{(4,56 - 0)}^2} + {{(28,52 - 24,4)}^2}} \approx 6,15\)
Vậy sau 10 phút, khoảng cách giữa hai chú kiến là khoảng 6,15 m (làm tròn đến hàng phần trăm).
Bài tập 5.42 trang 85 SGK Toán 12 tập 2 là một bài toán điển hình trong chương trình học về đạo hàm của hàm số. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Trước khi đi vào giải bài toán cụ thể, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài toán 5.42 thường yêu cầu chúng ta:
Để minh họa, giả sử bài toán 5.42 có nội dung như sau:
Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
y' = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta thấy:
Ngoài bài tập 5.42, còn rất nhiều bài tập tương tự về đạo hàm trong SGK Toán 12 tập 2. Để giải quyết các bài tập này, các em có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, các em có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ từ các thầy cô giáo.
Bài tập 5.42 trang 85 SGK Toán 12 tập 2 là một bài toán quan trọng giúp các em hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, các em sẽ tự tin hơn trong việc học tập môn Toán 12.