Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 55, 56, 57, 58 SGK Toán 12 tập 1. Các em hãy chuẩn bị SGK và cùng chúng tôi bắt đầu nhé!
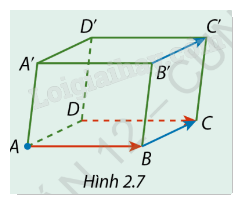
Cho hình hộp ABCD.A'B'C'D' (Hình 2.7). Một vật bắt đầu di chuyển từ điểm A theo độ dịch chuyển bằng \(\overrightarrow {DC} \), sau đó tiếp tục di chuyển theo độ dịch chuyển bằng \(\overrightarrow {B'C'} \). Hỏi vật sẽ di chuyển đến điểm nào?
Trả lời câu hỏi Luyện tập 1 trang 56 SGK Toán 12 Cùng khám phá
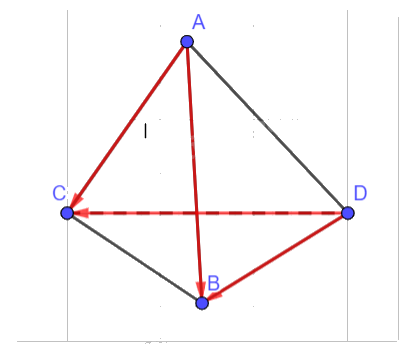
Cho tứ diện ABCD. Chứng minh rằng \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC} \).
Phương pháp giải:
- Áp dụng quy tắc ba điểm.
- Sử dụng tính chất kết hợp và giao hoán của phép cộng vectơ.
Lời giải chi tiết:
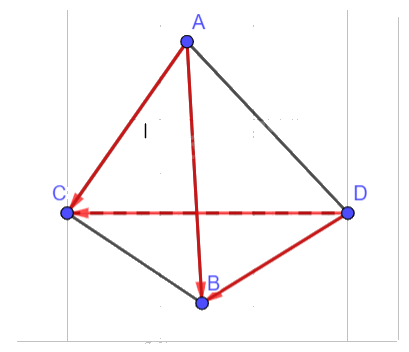
- Áp dụng quy tắc ba điểm, ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {BC} \).
- Sử dụng tính chất kết hợp và giao hoán của phép cộng vectơ, ta suy ra: \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC} \).
Trả lời câu hỏi Hoạt động 1 trang 55 SGK Toán 12 Cùng khám phá
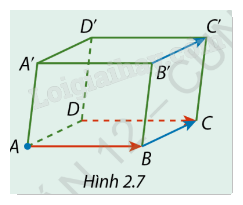
Cho hình hộp ABCD.A'B'C'D' (Hình 2.7). Một vật bắt đầu di chuyển từ điểm A theo độ dịch chuyển bằng \(\overrightarrow {DC} \), sau đó tiếp tục di chuyển theo độ dịch chuyển bằng \(\overrightarrow {B'C'} \). Hỏi vật sẽ di chuyển đến điểm nào?
Phương pháp giải:
1. Xác định điểm đến sau khi di chuyển theo vectơ đầu tiên.
2. Xác định điểm đến tiếp theo sau khi di chuyển theo vectơ thứ hai.
Lời giải chi tiết:
Bước 1: Di chuyển từ A theo độ dịch chuyển \(\overrightarrow {DC} \)
Điểm A dịch chuyển theo \(\overrightarrow {DC} \) tức là di chuyển theo đoạn DC nhưng bắt đầu từ A. Vì \(D\) và A nằm trên cùng một mặt phẳng, nên khi dịch chuyển từ A theo độ dịch chuyển \(\overrightarrow {DC} \), vật sẽ đến điểm B (do A, D, B, C tạo thành một hình chữ nhật).
Bước 2: Di chuyển tiếp tục từ B theo độ dịch chuyển \(\overrightarrow {B'C'} \)
Điểm B dịch chuyển theo \(\overrightarrow {B'C'} \) tức là di chuyển theo đoạn B'C' nhưng bắt đầu từ B. Do B và B’ nằm trên cùng một mặt phẳng, nên khi dịch chuyển từ B theo độ dịch chuyển \(\overrightarrow {B'C'} \), vật sẽ đến điểm C (do B, B', C, C' tạo thành một hình chữ nhật).
Vậy, sau khi thực hiện hai bước di chuyển, vật sẽ đến điểm C.
Trả lời câu hỏi Luyện tập 2 trang 57 SGK Toán 12 Cùng khám phá
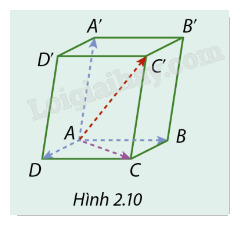
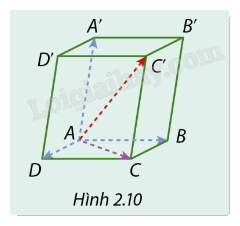
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10). Tìm vectơ \(\overrightarrow {BA} + \overrightarrow {B'C'} + \overrightarrow {DD'} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp vào hình hộp ABCD.A’B’C’D’.
Lời giải chi tiết:
Vì BB’C’C là hình chữ nhật nên \(\overrightarrow {BC} = \overrightarrow {B'C'} \).
Vì BB’D’D là hình chữ nhật nên \(\overrightarrow {D'D} = \overrightarrow {B'B} \).
Thay \(\overrightarrow {BC} = \overrightarrow {B'C'} \) và \(\overrightarrow {D'D} = \overrightarrow {B'B} \) , đồng thời áp dụng quy tắc hình hộp, ta suy ra:
\(\overrightarrow {BA} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \).
Trả lời câu hỏi Hoạt động 2 trang 56 SGK Toán 12 Cùng khám phá
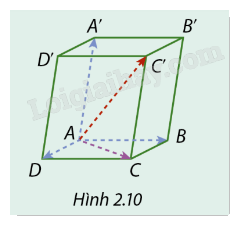
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10).
a) Tìm liên hệ giữa \(\overrightarrow {AD} + \overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Phương pháp giải:
a) Áp dụng quy tắc hình bình hành.
b) Sử dụng mối liên hệ đã chứng minh ở câu a và phép cộng của hai vectơ.
Lời giải chi tiết:
a) Trong hình hộp ABCD.A’B’C’D’ thì có đáy ABCD là hình bình hành.
Áp dụng quy tắc hình bình hành, ta được: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
b) Sử dụng phép cộng của hai vectơ, ta suy ra:
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {CC'} = \overrightarrow {AC'} \).
Trả lời câu hỏi Hoạt động 3 trang 57 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10). Tìm tổng của vectơ \(\overrightarrow {AD} \) và vectơ đối của \(\overrightarrow {C'C} \).
Phương pháp giải:
- Sử dụng các tính chất của hình hộp.
- Xác định vectơ đối của \(\overrightarrow {C'C} \) dựa trên khái niệm: “Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).”
- Áp dụng các tính chất của phép cộng hai vectơ và quy tắc hình bình hành.
Lời giải chi tiết:
- Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên: \(\overrightarrow {C'C} = \overrightarrow {A'A} \).
- Suy ra vectơ đối của \(\overrightarrow {C'C} \) cũng là vectơ đối của \(\overrightarrow {A'A} \).
- Áp dụng các tính chất của phép cộng hai vectơ và quy tắc hình bình hành, ta suy ra: \(\overrightarrow {AD} + \left( { - \overrightarrow {C'C} } \right) = \overrightarrow {AD} + \left( { - \overrightarrow {A'A} } \right) = \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD'} \).
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
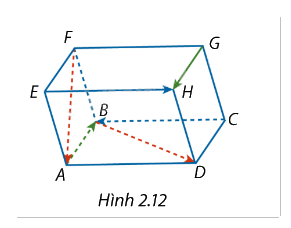
Cho hình hộp ABCD.EFGH (Hình 2.12). Hãy tìm:
a) \(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \);
b) \(\overrightarrow {FA} - \overrightarrow {BD} \).
Phương pháp giải:
1. Sử dụng tính chất của các vectơ trong hình hộp để xác định các vectơ cần tìm.
2. Áp dụng quy tắc cộng và trừ vectơ.
Lời giải chi tiết:
a) Tìm \(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \):
Ta có:
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {CB} = \overrightarrow {DA} \)
và
\(\overrightarrow {GH} = \overrightarrow {FE} ,\overrightarrow {EH} = \overrightarrow {FG} \)
Nên:
\(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} = \overrightarrow {DC} + \overrightarrow {DA} + \overrightarrow {FE} + \overrightarrow {FG} = \overrightarrow {DB} + \overrightarrow {FH} = \overrightarrow {DB} - \overrightarrow {DB} = \overrightarrow 0 \)
b) Tìm \(\overrightarrow {FA} - \overrightarrow {BD} \):
Ta có:
\(\overrightarrow {FA} = \overrightarrow {FE} + \overrightarrow {EA} \)
và
\(\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD} \)
Nên:
\(\overrightarrow {FA} - \overrightarrow {BD} = (\overrightarrow {FE} + \overrightarrow {EA} ) - (\overrightarrow {BC} + \overrightarrow {CD} )\)
Vì ABCD.EFGH là hình hộp nên ta có:\(\overrightarrow {FE} = \overrightarrow {CD} ,\overrightarrow {EA} = \overrightarrow {FB} \)
Do đó:
\(\overrightarrow {FA} - \overrightarrow {BD} = (\overrightarrow {CD} + \overrightarrow {FB} ) - (\overrightarrow {BC} + \overrightarrow {CD} ) = \overrightarrow {FB} - \overrightarrow {BC} = \overrightarrow {FB} - \overrightarrow {FG} = \overrightarrow {GB} \).
Trả lời câu hỏi Hoạt động 1 trang 55 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.A'B'C'D' (Hình 2.7). Một vật bắt đầu di chuyển từ điểm A theo độ dịch chuyển bằng \(\overrightarrow {DC} \), sau đó tiếp tục di chuyển theo độ dịch chuyển bằng \(\overrightarrow {B'C'} \). Hỏi vật sẽ di chuyển đến điểm nào?
Phương pháp giải:
1. Xác định điểm đến sau khi di chuyển theo vectơ đầu tiên.
2. Xác định điểm đến tiếp theo sau khi di chuyển theo vectơ thứ hai.
Lời giải chi tiết:
Bước 1: Di chuyển từ A theo độ dịch chuyển \(\overrightarrow {DC} \)
Điểm A dịch chuyển theo \(\overrightarrow {DC} \) tức là di chuyển theo đoạn DC nhưng bắt đầu từ A. Vì \(D\) và A nằm trên cùng một mặt phẳng, nên khi dịch chuyển từ A theo độ dịch chuyển \(\overrightarrow {DC} \), vật sẽ đến điểm B (do A, D, B, C tạo thành một hình chữ nhật).
Bước 2: Di chuyển tiếp tục từ B theo độ dịch chuyển \(\overrightarrow {B'C'} \)
Điểm B dịch chuyển theo \(\overrightarrow {B'C'} \) tức là di chuyển theo đoạn B'C' nhưng bắt đầu từ B. Do B và B’ nằm trên cùng một mặt phẳng, nên khi dịch chuyển từ B theo độ dịch chuyển \(\overrightarrow {B'C'} \), vật sẽ đến điểm C (do B, B', C, C' tạo thành một hình chữ nhật).
Vậy, sau khi thực hiện hai bước di chuyển, vật sẽ đến điểm C.
Trả lời câu hỏi Luyện tập 1 trang 56 SGK Toán 12 Cùng khám phá
Cho tứ diện ABCD. Chứng minh rằng \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC} \).
Phương pháp giải:
- Áp dụng quy tắc ba điểm.
- Sử dụng tính chất kết hợp và giao hoán của phép cộng vectơ.
Lời giải chi tiết:
- Áp dụng quy tắc ba điểm, ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {BC} \).
- Sử dụng tính chất kết hợp và giao hoán của phép cộng vectơ, ta suy ra: \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC} \).
Trả lời câu hỏi Hoạt động 2 trang 56 SGK Toán 12 Cùng khám phá
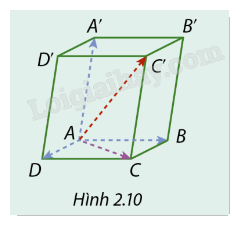
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10).
a) Tìm liên hệ giữa \(\overrightarrow {AD} + \overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Phương pháp giải:
a) Áp dụng quy tắc hình bình hành.
b) Sử dụng mối liên hệ đã chứng minh ở câu a và phép cộng của hai vectơ.
Lời giải chi tiết:
a) Trong hình hộp ABCD.A’B’C’D’ thì có đáy ABCD là hình bình hành.
Áp dụng quy tắc hình bình hành, ta được: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
b) Sử dụng phép cộng của hai vectơ, ta suy ra:
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {CC'} = \overrightarrow {AC'} \).
Trả lời câu hỏi Luyện tập 2 trang 57 SGK Toán 12 Cùng khám phá
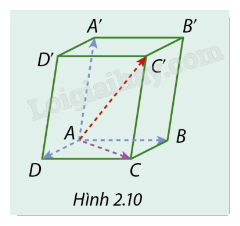
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10). Tìm vectơ \(\overrightarrow {BA} + \overrightarrow {B'C'} + \overrightarrow {DD'} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp vào hình hộp ABCD.A’B’C’D’.
Lời giải chi tiết:
Vì BB’C’C là hình chữ nhật nên \(\overrightarrow {BC} = \overrightarrow {B'C'} \).
Vì BB’D’D là hình chữ nhật nên \(\overrightarrow {D'D} = \overrightarrow {B'B} \).
Thay \(\overrightarrow {BC} = \overrightarrow {B'C'} \) và \(\overrightarrow {D'D} = \overrightarrow {B'B} \) , đồng thời áp dụng quy tắc hình hộp, ta suy ra:
\(\overrightarrow {BA} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \).
Trả lời câu hỏi Hoạt động 3 trang 57 SGK Toán 12 Cùng khám phá
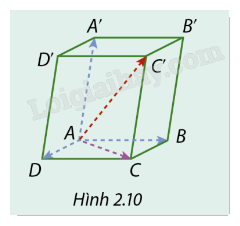
Cho hình hộp ABCD.A’B’C’D’ (Hình 2.10). Tìm tổng của vectơ \(\overrightarrow {AD} \) và vectơ đối của \(\overrightarrow {C'C} \).
Phương pháp giải:
- Sử dụng các tính chất của hình hộp.
- Xác định vectơ đối của \(\overrightarrow {C'C} \) dựa trên khái niệm: “Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).”
- Áp dụng các tính chất của phép cộng hai vectơ và quy tắc hình bình hành.
Lời giải chi tiết:
- Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên: \(\overrightarrow {C'C} = \overrightarrow {A'A} \).
- Suy ra vectơ đối của \(\overrightarrow {C'C} \) cũng là vectơ đối của \(\overrightarrow {A'A} \).
- Áp dụng các tính chất của phép cộng hai vectơ và quy tắc hình bình hành, ta suy ra: \(\overrightarrow {AD} + \left( { - \overrightarrow {C'C} } \right) = \overrightarrow {AD} + \left( { - \overrightarrow {A'A} } \right) = \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD'} \).
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
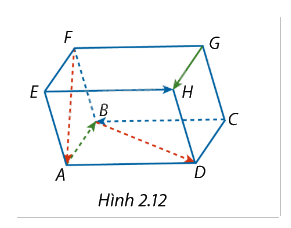
Cho hình hộp ABCD.EFGH (Hình 2.12). Hãy tìm:
a) \(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \);
b) \(\overrightarrow {FA} - \overrightarrow {BD} \).
Phương pháp giải:
1. Sử dụng tính chất của các vectơ trong hình hộp để xác định các vectơ cần tìm.
2. Áp dụng quy tắc cộng và trừ vectơ.
Lời giải chi tiết:
a) Tìm \(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \):
Ta có:
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {CB} = \overrightarrow {DA} \)
và
\(\overrightarrow {GH} = \overrightarrow {FE} ,\overrightarrow {EH} = \overrightarrow {FG} \)
Nên:
\(\overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} = \overrightarrow {DC} + \overrightarrow {DA} + \overrightarrow {FE} + \overrightarrow {FG} = \overrightarrow {DB} + \overrightarrow {FH} = \overrightarrow {DB} - \overrightarrow {DB} = \overrightarrow 0 \)
b) Tìm \(\overrightarrow {FA} - \overrightarrow {BD} \):
Ta có:
\(\overrightarrow {FA} = \overrightarrow {FE} + \overrightarrow {EA} \)
và
\(\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD} \)
Nên:
\(\overrightarrow {FA} - \overrightarrow {BD} = (\overrightarrow {FE} + \overrightarrow {EA} ) - (\overrightarrow {BC} + \overrightarrow {CD} )\)
Vì ABCD.EFGH là hình hộp nên ta có:\(\overrightarrow {FE} = \overrightarrow {CD} ,\overrightarrow {EA} = \overrightarrow {FB} \)
Do đó:
\(\overrightarrow {FA} - \overrightarrow {BD} = (\overrightarrow {CD} + \overrightarrow {FB} ) - (\overrightarrow {BC} + \overrightarrow {CD} ) = \overrightarrow {FB} - \overrightarrow {BC} = \overrightarrow {FB} - \overrightarrow {FG} = \overrightarrow {GB} \).
Trả lời câu hỏi Vận dụng 1 trang 58 SGK Toán 12 Cùng khám phá
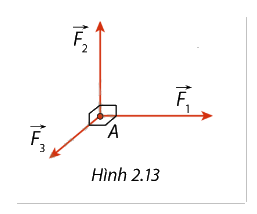
Một chất điểm chịu tác động bởi 3 lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có chung điểm đặt \(A\) và có giá vuông góc với nhau từng đôi một. Biết cường độ của các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) lần lượt là 10 N, 8 N và 5 N, xác định hợp lực của 3 lực và tính cường độ của hợp lực (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải:
- Vì các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có giá vuông góc với nhau từng đôi một, ta có thể coi chúng là các cạnh của một hình hộp chữ nhật trong không gian.
- Hợp lực \(\vec F\) của 3 lực này sẽ là đường chéo của hình hộp chữ nhật đó.
- Tính hợp lực: \(\left| {\overrightarrow F } \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + {{\left| {\overrightarrow {{F_3}} } \right|}^2}} \)
Lời giải chi tiết:
Hợp lực \(\vec F\) của 3 lực này sẽ là đường chéo của hình hộp chữ nhật tạo bởi 3 lực đó.
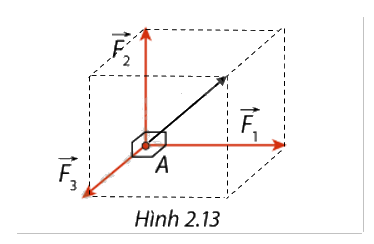
Xác định độ lớn của các lực:
\(|\overrightarrow {{F_1}} | = 10{\rm{N}}\)
\(|\overrightarrow {{F_2}} | = 8{\rm{N}}\)
\(|\overrightarrow {{F_3}} | = 5{\rm{N}}\)
Tính hợp lực:
\(\left| {\overrightarrow F } \right| = \sqrt {{{10}^2} + {8^2} + {5^2}} = \sqrt {189} \approx 14N\)
Vậy hợp lực của 3 lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có cường độ xấp xỉ \(14{\rm{N}}\).
Trả lời câu hỏi Vận dụng 1 trang 58 SGK Toán 12 Cùng khám phá
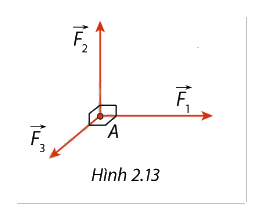
Một chất điểm chịu tác động bởi 3 lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có chung điểm đặt \(A\) và có giá vuông góc với nhau từng đôi một. Biết cường độ của các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) lần lượt là 10 N, 8 N và 5 N, xác định hợp lực của 3 lực và tính cường độ của hợp lực (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải:
- Vì các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có giá vuông góc với nhau từng đôi một, ta có thể coi chúng là các cạnh của một hình hộp chữ nhật trong không gian.
- Hợp lực \(\vec F\) của 3 lực này sẽ là đường chéo của hình hộp chữ nhật đó.
- Tính hợp lực: \(\left| {\overrightarrow F } \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + {{\left| {\overrightarrow {{F_3}} } \right|}^2}} \)
Lời giải chi tiết:
Hợp lực \(\vec F\) của 3 lực này sẽ là đường chéo của hình hộp chữ nhật tạo bởi 3 lực đó.
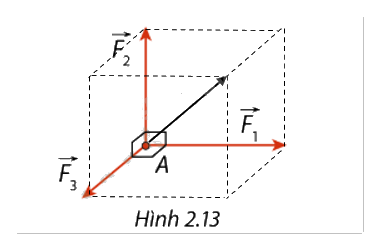
Xác định độ lớn của các lực:
\(|\overrightarrow {{F_1}} | = 10{\rm{N}}\)
\(|\overrightarrow {{F_2}} | = 8{\rm{N}}\)
\(|\overrightarrow {{F_3}} | = 5{\rm{N}}\)
Tính hợp lực:
\(\left| {\overrightarrow F } \right| = \sqrt {{{10}^2} + {8^2} + {5^2}} = \sqrt {189} \approx 14N\)
Vậy hợp lực của 3 lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) có cường độ xấp xỉ \(14{\rm{N}}\).
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào các kiến thức cơ bản về đạo hàm, bao gồm định nghĩa, ý nghĩa hình học và các quy tắc tính đạo hàm của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Các bài tập trên trang 55 thường yêu cầu học sinh vận dụng định nghĩa đạo hàm để tính đạo hàm của hàm số tại một điểm. Để giải quyết các bài tập này, học sinh cần nắm vững công thức tính đạo hàm theo định nghĩa và thực hành tính toán một cách cẩn thận.
Trang 56 tập trung vào việc ứng dụng đạo hàm để tìm hệ số góc của tiếp tuyến của đồ thị hàm số tại một điểm. Học sinh cần hiểu rõ mối liên hệ giữa đạo hàm và hệ số góc của tiếp tuyến.
Trang 57 giới thiệu các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số. Học sinh cần nắm vững các quy tắc này để tính đạo hàm một cách nhanh chóng và chính xác.
| Quy tắc | Công thức |
|---|---|
| Quy tắc tổng | (u + v)' = u' + v' |
| Quy tắc hiệu | (u - v)' = u' - v' |
Trang 58 là phần tổng hợp các bài tập vận dụng các kiến thức đã học về đạo hàm. Các bài tập này thường có độ khó cao hơn và yêu cầu học sinh phải có khả năng phân tích và giải quyết vấn đề.
Bài 5: Tính đạo hàm của hàm số y = (x2 + 1)(x - 2).
Bài 6: Tính đạo hàm của hàm số y = x2 / (x + 1).
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 55, 56, 57, 58 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!