Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Mục 2 trang 5,6,7 SGK Toán 12 tập 1 là một phần quan trọng trong chương trình học, đòi hỏi sự nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải đáp này, giúp bạn tự tin chinh phục các bài tập Toán 12.
Cực trị của hàm số
Trả lời câu hỏi Luyện tập 3 trang 6 SGK Toán 12 Kết nối tri thức
Chỉ ra một điểm cực đại, một điểm cực tiểu của đồ thị hàm số được cho ở hoạt động 3
Phương pháp giải:
Áp dụng định nghĩa về cực trị:
Cho hàm số \(y = f(x)\)liên tục trên khoảng \((a;b)\) và điểm \({x_0} \in (a;b)\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) < f({x_0})\)với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt cực đại tại \({x_0}\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) > f({x_0})\) với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt tiểu đại tại \({x_0}\)
Lời giải chi tiết:
Theo định nghĩa, ta có thể chọn\(h = 1\) ta có, \({x_0} - h = - 3\)và \({x_0} + h = - 1\)
Dựa vào đồ thị hàm số, ta có
\(f(x) > f( - 2)\), với\(\forall x \in ( - 3; - 1)\backslash \{ - 2\} \)
Suy ra \({x_0} = - 2\) là điểm cực tiểu của đồ thị hàm số
Theo định nghĩa, ta có thể chọn \(h = \frac{1}{2}\) ta có, \({x_0} - h = \frac{3}{2}\) và\({x_0} + h = \frac{5}{2}\)
Dựa vào đồ thị hàm số, ta có
\(f(x) < f(2)\) với \(\forall x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\backslash \{ 2\} \)
Suy ra \({x_0} = 2\) là điểm đại của đồ thị hàm số
Trả lời câu hỏi Luyện tập 5 trang 8 SGK Toán 12 Kết nối tri thức
Tìm cực trị của hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\)
Phương pháp giải:
Bước 1: Tính \(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định cực trị của hàm số
Lời giải chi tiết:
Hàm số trên xác định trên \(R/\{ 2\} \)
Ta có: \(f'(x) = \frac{{3(x - 2) - (3x + 1)}}{{{{(x - 2)}^2}}}\)
\(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}}\)
Vì \(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}} < 0\) với \(x \in R/\{ 2\} \)
Nên hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\) không có cực trị.
Trả lời câu hỏi Luyện tập 4 trang 7 SGK Toán 12 Kết nối tri thức
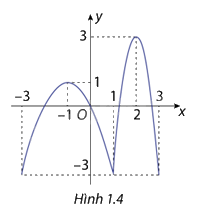
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ { - 3;3} \right]\)và có đồ thị hàm số như hình 1.4. Hãy xác định các điểm cực trị của hàm số trên khoảng\(\left( { - 3;3} \right)\)
Phương pháp giải:
Dựa vào đồ thị hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số, hàm số có 3 điểm cực trị là-1;1;2
Với điểm có cực trị là -1 thì giá trị cực trị là 1
Với điểm có cực trị là 1 thì giá trị cực trị là -3
Với điểm có cực trị là 2 thì giá trị cực trị là 3
Trả lời câu hỏi Vận dụng trang 8 SGK Toán 12 Kết nối tri thức
Trở lại bài toán Khởi động ban đầu bài học, hãy lập bảng biến thiên của hàm số \(y = C(x) = \frac{{30x}}{{{x^2} + 2}}\)trên khoảng \((0; + \infty )\)
Khi đó, cho biết hàm nồng độ thước trong máu :
a) Tăng trong khoảng thời gian nào
b) Đạt giá trị cực đại là bao nhiêu trong khoảng thời gian 6 phút sau khi tiêm
Phương pháp giải:
Bước 1: Tính \(C'(x)\)
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính hàm nồng độ thước trong máu tăng trong khoảng thời gian nào là tính hàm số \(C(x)\) tăng trong khoảng nào hay hàm số \(C(x)\)đồng biến trong khoảng nào
Bước 4: Nồng độ thước máu đạt cực đại là bao nhiêu trong 6 phút sau khi tiêm là giá trị cực đại của hàm số \(C(x)\) trong khoảng \((0;6)\)
Lời giải chi tiết:
Hàm số trên xác định trên R
Ta có: \(y' = C'(x) = \frac{{30({x^2} + 2) - 30x.2x}}{{{{({x^2} + 2)}^2}}}\)
\( = \frac{{ - 30{x^2} + 60}}{{{{({x^2} + 2)}^2}}}\)
Xét \(y' = 0\) \( \Rightarrow - 30{x^2} + 60 = 0\) \( \Leftrightarrow x = \sqrt 2 \)
Ta có bảng biến thiên:
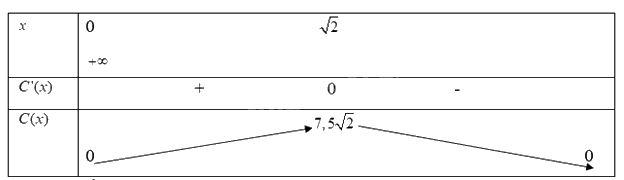
Từ bảng biến thiên, ta có :
a) Hàm số \(C(x)\)đồng biến trên khoảng \((0;7,5\sqrt 2 )\)hay nồng độ thước máu tăng từ sau khi tiêm đến \(7,5\sqrt 2 \)phút sau.
b) Hàm số \(C(x)\) đạt giá trị cực đại tại \(x = \sqrt 2 \)hay nồng độ thức máu đạt giá trị cực đại sau \(\sqrt 2 \) phút
Trả lời câu hỏi Hoạt động 3 trang 5 SGK Toán 12 Kết nối tri thức
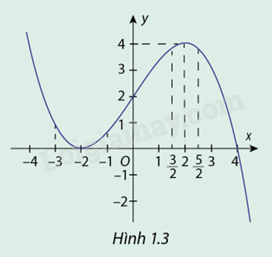
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Phương pháp giải:
a) Tính \(f'(x)\) rồi giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị hàm số rồi giải
Lời giải chi tiết:
a) Ta có: \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2}\)
Xét \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2} = 0\)
\( \Rightarrow {x^2} = 4\)
\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
b) Dựa vào đồ thị, giá trị của \(f( - 2)\) luôn bé hơn các giá trị \(f(x)\) khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, giá trị của \(f(2)\)luôn lớn hơn các giá trị\(f(x)\) khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Trả lời câu hỏi Hoạt động 4 trang 6 SGK Toán 12 Kết nối tri thức
Xét hàm số ở hoạt động 3. Xác định dấu của đạo hàm ở các ô 
tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
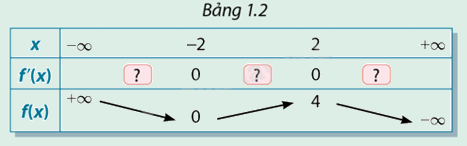
Phương pháp giải:
Dựa vào đồ thị hàm số, nếu đồ thị hàm số\(f(x)\) đi xuống thì \(f'(x)\)mang dấu (-)và ngược lại, nếu đồ thị hàm số\(f(x)\) đi lên thì \(f'(x)\) mang dấu (+).
Nhìn vào điểm cực trị trên bảng biến thiên rồi nhận xét.
Lời giải chi tiết:
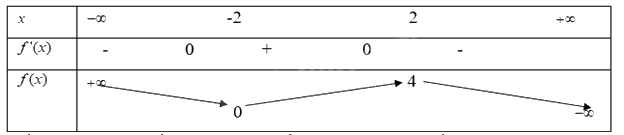
Mối liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm là: Nếu đạo hàm có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Trả lời câu hỏi Hoạt động 3 trang 5 SGK Toán 12 Kết nối tri thức
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
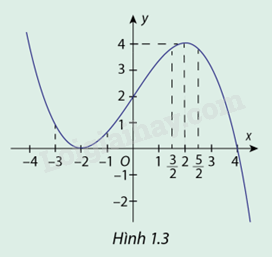
Phương pháp giải:
a) Tính \(f'(x)\) rồi giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị hàm số rồi giải
Lời giải chi tiết:
a) Ta có: \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2}\)
Xét \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2} = 0\)
\( \Rightarrow {x^2} = 4\)
\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
b) Dựa vào đồ thị, giá trị của \(f( - 2)\) luôn bé hơn các giá trị \(f(x)\) khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, giá trị của \(f(2)\)luôn lớn hơn các giá trị\(f(x)\) khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Trả lời câu hỏi Luyện tập 3 trang 6 SGK Toán 12 Kết nối tri thức
Chỉ ra một điểm cực đại, một điểm cực tiểu của đồ thị hàm số được cho ở hoạt động 3
Phương pháp giải:
Áp dụng định nghĩa về cực trị:
Cho hàm số \(y = f(x)\)liên tục trên khoảng \((a;b)\) và điểm \({x_0} \in (a;b)\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) < f({x_0})\)với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt cực đại tại \({x_0}\)
Nếu tồn tại \(h > 0\)sao cho \(f(x) > f({x_0})\) với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt tiểu đại tại \({x_0}\)
Lời giải chi tiết:
Theo định nghĩa, ta có thể chọn\(h = 1\) ta có, \({x_0} - h = - 3\)và \({x_0} + h = - 1\)
Dựa vào đồ thị hàm số, ta có
\(f(x) > f( - 2)\), với\(\forall x \in ( - 3; - 1)\backslash \{ - 2\} \)
Suy ra \({x_0} = - 2\) là điểm cực tiểu của đồ thị hàm số
Theo định nghĩa, ta có thể chọn \(h = \frac{1}{2}\) ta có, \({x_0} - h = \frac{3}{2}\) và\({x_0} + h = \frac{5}{2}\)
Dựa vào đồ thị hàm số, ta có
\(f(x) < f(2)\) với \(\forall x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\backslash \{ 2\} \)
Suy ra \({x_0} = 2\) là điểm đại của đồ thị hàm số
Trả lời câu hỏi Hoạt động 4 trang 6 SGK Toán 12 Kết nối tri thức
Xét hàm số ở hoạt động 3. Xác định dấu của đạo hàm ở các ô 
tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
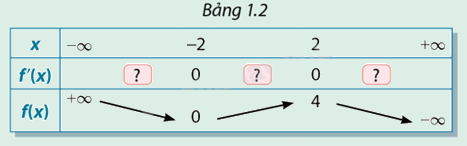
Phương pháp giải:
Dựa vào đồ thị hàm số, nếu đồ thị hàm số\(f(x)\) đi xuống thì \(f'(x)\)mang dấu (-)và ngược lại, nếu đồ thị hàm số\(f(x)\) đi lên thì \(f'(x)\) mang dấu (+).
Nhìn vào điểm cực trị trên bảng biến thiên rồi nhận xét.
Lời giải chi tiết:
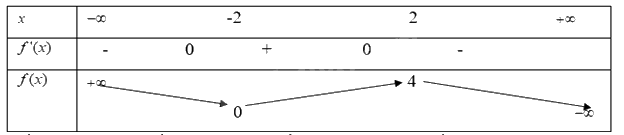
Mối liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm là: Nếu đạo hàm có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Trả lời câu hỏi Luyện tập 4 trang 7 SGK Toán 12 Kết nối tri thức
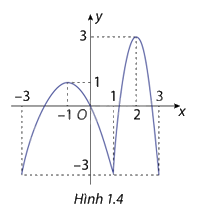
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ { - 3;3} \right]\)và có đồ thị hàm số như hình 1.4. Hãy xác định các điểm cực trị của hàm số trên khoảng\(\left( { - 3;3} \right)\)
Phương pháp giải:
Dựa vào đồ thị hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số, hàm số có 3 điểm cực trị là-1;1;2
Với điểm có cực trị là -1 thì giá trị cực trị là 1
Với điểm có cực trị là 1 thì giá trị cực trị là -3
Với điểm có cực trị là 2 thì giá trị cực trị là 3
Trả lời câu hỏi Luyện tập 5 trang 8 SGK Toán 12 Kết nối tri thức
Tìm cực trị của hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\)
Phương pháp giải:
Bước 1: Tính \(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định cực trị của hàm số
Lời giải chi tiết:
Hàm số trên xác định trên \(R/\{ 2\} \)
Ta có: \(f'(x) = \frac{{3(x - 2) - (3x + 1)}}{{{{(x - 2)}^2}}}\)
\(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}}\)
Vì \(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}} < 0\) với \(x \in R/\{ 2\} \)
Nên hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\) không có cực trị.
Trả lời câu hỏi Vận dụng trang 8 SGK Toán 12 Kết nối tri thức
Trở lại bài toán Khởi động ban đầu bài học, hãy lập bảng biến thiên của hàm số \(y = C(x) = \frac{{30x}}{{{x^2} + 2}}\)trên khoảng \((0; + \infty )\)
Khi đó, cho biết hàm nồng độ thước trong máu :
a) Tăng trong khoảng thời gian nào
b) Đạt giá trị cực đại là bao nhiêu trong khoảng thời gian 6 phút sau khi tiêm
Phương pháp giải:
Bước 1: Tính \(C'(x)\)
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính hàm nồng độ thước trong máu tăng trong khoảng thời gian nào là tính hàm số \(C(x)\) tăng trong khoảng nào hay hàm số \(C(x)\)đồng biến trong khoảng nào
Bước 4: Nồng độ thước máu đạt cực đại là bao nhiêu trong 6 phút sau khi tiêm là giá trị cực đại của hàm số \(C(x)\) trong khoảng \((0;6)\)
Lời giải chi tiết:
Hàm số trên xác định trên R
Ta có: \(y' = C'(x) = \frac{{30({x^2} + 2) - 30x.2x}}{{{{({x^2} + 2)}^2}}}\)
\( = \frac{{ - 30{x^2} + 60}}{{{{({x^2} + 2)}^2}}}\)
Xét \(y' = 0\) \( \Rightarrow - 30{x^2} + 60 = 0\) \( \Leftrightarrow x = \sqrt 2 \)
Ta có bảng biến thiên:
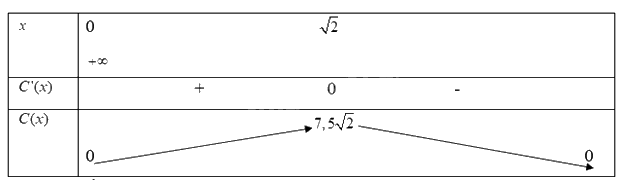
Từ bảng biến thiên, ta có :
a) Hàm số \(C(x)\)đồng biến trên khoảng \((0;7,5\sqrt 2 )\)hay nồng độ thước máu tăng từ sau khi tiêm đến \(7,5\sqrt 2 \)phút sau.
b) Hàm số \(C(x)\) đạt giá trị cực đại tại \(x = \sqrt 2 \)hay nồng độ thức máu đạt giá trị cực đại sau \(\sqrt 2 \) phút
Mục 2 của SGK Toán 12 tập 1 thường tập trung vào các kiến thức cơ bản về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Để giúp các em học sinh hiểu rõ hơn về nội dung này, giaitoan.edu.vn xin trình bày chi tiết lời giải cho từng bài tập trong mục 2 trang 5,6,7 SGK Toán 12 tập 1:
Bài tập này yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai dựa vào phương trình tổng quát y = ax2 + bx + c. Để giải bài tập này, các em cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số.
Bài tập này yêu cầu học sinh tìm tập xác định của hàm số bậc hai. Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x sao cho biểu thức trong hàm số có nghĩa. Trong trường hợp hàm số bậc hai, tập xác định là tập R (tập hợp tất cả các số thực).
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc hai. Để vẽ đồ thị hàm số bậc hai, các em cần xác định các yếu tố quan trọng như đỉnh, trục đối xứng, giao điểm với trục hoành và trục tung. Sau đó, các em có thể vẽ đồ thị bằng cách sử dụng các điểm đã xác định.
Bài tập này yêu cầu học sinh tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số bậc hai. Để giải bài tập này, các em cần sử dụng các công thức và phương pháp liên quan đến đỉnh của parabol. Nếu a > 0, hàm số có giá trị nhỏ nhất tại đỉnh. Nếu a < 0, hàm số có giá trị lớn nhất tại đỉnh.
Để giải bài tập hàm số bậc hai hiệu quả, các em cần:
Hàm số bậc hai có nhiều ứng dụng trong thực tế, chẳng hạn như:
Khi giải bài tập hàm số bậc hai, các em cần lưu ý:
Hy vọng rằng với bộ giải đáp chi tiết và các phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 12. Chúc các em học tốt!
