Chào mừng các em học sinh đến với bài giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về hàm số và đồ thị.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét( h>0)và 2 đầu là các nữa hình cầu bán kính r (r>0)(Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 ({m^3}). Để sơn mắt ngoài phần hình cầu cần 20 000cho 1 ({m^2}) , còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 ({m^2}).Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa( bao gồm diện tích xung quanh hình trụ và diện tích 2 nữa hình cầu) là nhỏ nhất, biết rằng bán kính r không đư
Đề bài
Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét (h > 0) và 2 đầu là các nửa hình cầu bán kính r (r > 0) (Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 \({m^3}\). Để sơn mắt ngoài phần hình cầu cần 20 000 cho 1 \({m^2}\), còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 \({m^2}\). Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa (bao gồm diện tích xung quanh hình trụ và diện tích 2 nửa hình cầu) là nhỏ nhất, biết rằng bán kính r không được vượt quá 50m.
Phương pháp giải - Xem chi tiết
Bước 1: Lập công thức tính chi phí sơn.
Bước 2: Lập bảng biến thiên của hàm số.
Bước 3: Tính chi phí nhỏ nhất để sơn là tìm giá trị nhỏ nhất của hàm số.
Lời giải chi tiết
Ta có thể tích thùng nhiên liệu là:
\(V = \frac{4}{3}{r^3}\pi + {r^2}\pi h \Leftrightarrow 144000\pi = \frac{4}{3}{r^3}\pi + {r^2}\pi h \Leftrightarrow h = \frac{{144000 - \frac{4}{3}{r^3}}}{{{r^2}}}\).
DIện tích xung quanh thùng nhiên liệu là là: \(S = 4{r^2}\pi + 2rh\pi \).
Số tiền cần để sơn xung quanh thùng nhiên liệu là:
\(T = 20000.4{r^2}\pi + 10000.2rh\pi = 80000{r^2}\pi + 20000rh\pi \left( {\frac{{144000 - \frac{4}{3}{r^3}}}{{{r^2}}}} \right)\)
\( = 80000{r^2}\pi + 2880000000\frac{\pi }{r} - \frac{{80000}}{3}{r^2}\pi = \frac{{160000}}{3}{r^2}\pi + 2880000000\frac{\pi }{r}\).
Bài toán trở thành tìm r để để hàm số T nhỏ nhất.
Ta có:
\(T' = \frac{{160000}}{3}\left( {2r} \right)\pi - 2880000000\frac{\pi }{{{r^2}}} = 0 \Leftrightarrow {r^3} = 27000 \Leftrightarrow r = 30\).
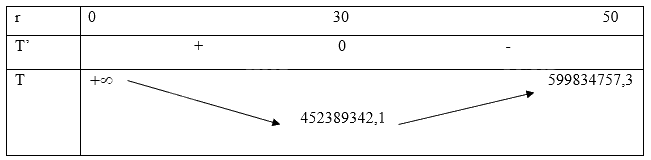
Vậy để chi phí sơn là nhỏ nhất thì r = 30.
Bài tập 1.11 trang 14 SGK Toán 12 tập 1 yêu cầu chúng ta xét tính đơn điệu của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm và các dấu hiệu xác định tính đơn điệu của hàm số.
Trước khi đi vào giải bài tập cụ thể, hãy cùng ôn lại một số kiến thức quan trọng:
Bài tập 1.11 thường yêu cầu xét tính đơn điệu của hàm số trên một khoảng xác định. Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Giả sử bài tập 1.11 là: Xét tính đơn điệu của hàm số y = x3 - 3x2 + 2.
Bước 1: Tập xác định
Hàm số y = x3 - 3x2 + 2 là hàm đa thức, xác định trên tập số thực R.
Bước 2: Tính đạo hàm
y' = 3x2 - 6x
Bước 3: Tìm điểm dừng và điểm không xác định
y' = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Hàm số y' xác định trên R.
Bước 4: Xét dấu đạo hàm
Ta có bảng xét dấu:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + |
Bước 5: Kết luận
Hàm số y = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và sách bài tập Toán 12 tập 1. Hãy chú ý đến việc phân tích bài toán, lựa chọn phương pháp giải phù hợp và kiểm tra lại kết quả.
Ngoài ra, các em có thể tham khảo thêm các tài liệu học tập trực tuyến, các video hướng dẫn giải bài tập trên giaitoan.edu.vn để hiểu rõ hơn về các kiến thức và kỹ năng giải toán.
Toán 12 là một môn học quan trọng, đòi hỏi sự chăm chỉ và kiên trì. Để học tốt môn Toán 12, các em nên: