Chào mừng các em học sinh đến với bài giải bài tập 2.4 trang 64 SGK Toán 12 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán về đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.
Cho hình hộp ABCD.EFGH. Đặt \(\overrightarrow {AB} = \vec a,\overrightarrow {AD} = \vec b,\overrightarrow {AE} = \vec c\). Gọi M là trung điểm của đoạn BG. Hãy biểu diễn \(\overrightarrow {AM} \) theo \(\vec a,\vec b,\vec c\).
Đề bài
Cho hình hộp ABCD.EFGH. Đặt \(\overrightarrow {AB} = \vec a,\overrightarrow {AD} = \vec b,\overrightarrow {AE} = \vec c\). Gọi M là trung điểm của đoạn BG. Hãy biểu diễn \(\overrightarrow {AM} \) theo \(\vec a,\vec b,\vec c\).
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc ba điểm, hình bình hành để biểu diễn \(\overrightarrow {AM} \) theo \(\vec a,\vec b,\vec c\).
Lời giải chi tiết
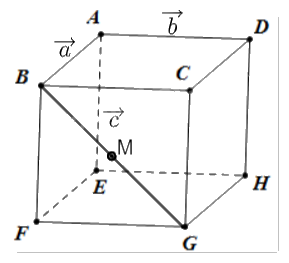
- Áp dụng quy tắc ba điểm, ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
- Vì M là trung điểm BG nên: \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BG} \)
- Mà ABCD.EFGH là hình hộp nên: \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AH} = \overrightarrow {AB} + \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AE} } \right) = \overrightarrow a + \frac{1}{2}\overrightarrow b + \frac{1}{2}\overrightarrow c \)
Bài tập 2.4 trang 64 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số hợp, đạo hàm của hàm số lượng giác và các quy tắc tính đạo hàm cơ bản để giải quyết các bài toán cụ thể. Việc nắm vững các công thức đạo hàm và kỹ năng biến đổi đại số là yếu tố then chốt để hoàn thành bài tập này.
Bài tập 2.4 bao gồm các câu hỏi trắc nghiệm và bài tập tự luận, yêu cầu học sinh:
Đề bài: Tính đạo hàm của hàm số y = sin(2x + 1).
Lời giải:
Sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Đặt u(v) = sin(v) và v(x) = 2x + 1.
Khi đó, u'(v) = cos(v) và v'(x) = 2.
Vậy, y' = cos(2x + 1) * 2 = 2cos(2x + 1).
Đề bài: Tính đạo hàm của hàm số y = cos2(x).
Lời giải:
Sử dụng quy tắc đạo hàm của hàm hợp và quy tắc đạo hàm của hàm số mũ:
y' = 2cos(x) * (-sin(x)) = -2cos(x)sin(x) = -sin(2x).
Đề bài: Tính đạo hàm của hàm số y = tan(x2 + 1).
Lời giải:
Sử dụng quy tắc đạo hàm của hàm hợp:
y' = (1/cos2(x2 + 1)) * (2x) = (2x)/cos2(x2 + 1).
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm, các em có thể tham khảo thêm các tài liệu sau:
Bài tập 2.4 trang 64 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.