Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 72 và 73 sách giáo khoa Toán 12 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu nhé!
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
Trả lời câu hỏi Luyện tập 1 trang 73 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt cầu (S) đi qua gốc toạ độ O, bán kính r = 5. Tìm toạ độ tâm I của (S), biết điểm I thuộc đường thẳng
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 4 + 2t}\end{array}} \right.\quad (t \in \mathbb{R}).\)
Phương pháp giải:
Gọi \(I(a,b,c)\) là tọa độ của tâm mặt cầu \(S\).
Vì mặt cầu \(S\) đi qua gốc tọa độ \(O(0,0,0)\), nên \(IO = r = 5\).
Đặt \(I\) nằm trên đường thẳng \(d\) và tìm giá trị \(t\) sao cho khoảng cách \(IO = 5\).
Giải phương trình để tìm \(t\), từ đó xác định tọa độ của \(I\).
Lời giải chi tiết:
Giả sử \(I(a,b,c)\) có tọa độ: \(a = 3 - t, b = t, c = 4 + 2t.\)
Do \(IO = 5\), ta có: \(IO = \sqrt {{a^2} + {b^2} + {c^2}} = 5.\)
Thay \(a = 3 - t\), \(b = t\), \(c = 4 + 2t\) vào phương trình:
\(\begin{array}{l}\sqrt {{{(3 - t)}^2} + {t^2} + {{(4 + 2t)}^2}} = 5.\\ \Leftrightarrow 9 - 6t + {t^2} + {t^2} + 16 + 16t + 4{t^2} = 25\\ \Leftrightarrow 6{t^2} + 10t + 25 = 25\\ \Leftrightarrow 2t(3t + 5) = 0\\ \Leftrightarrow t = 0,\,\,\,t = - \frac{5}{3}\end{array}\)
Vậy có hai toạ độ tâm I thoả mãn là \(I(3;0;4)\) hoặc \(I\left( {\frac{{14}}{3}; - \frac{5}{3};\frac{2}{3}} \right)\).
Trả lời câu hỏi Hoạt động 1 trang 72 SGK Toán 12 Cùng khám phá
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
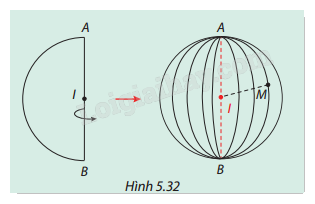
Phương pháp giải:
Khoảng cách từ tâm nửa đường tròn tới bất kỳ điểm nào nằm trên nửa đường tròn đều bằng nhau.
Lời giải chi tiết:
Vì M là vị trí của một điểm thuộc nửa đường tròn quay quanh AB, nên điểm M luôn có cùng khoảng cách từ I đến điểm đó như khoảng cách từ I đến bất kỳ điểm nào trên nửa đường tròn ban đầu, tức là IM = r.
Do bán kính không thay đổi trong suốt quá trình quay, khoảng cách từ I đến M vẫn giữ nguyên giá trị là 𝑟.
Trả lời câu hỏi Hoạt động 1 trang 72 SGK Toán 12 Cùng khám phá
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
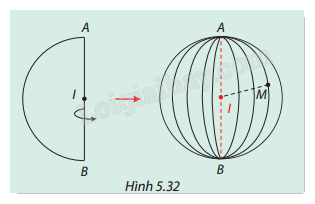
Phương pháp giải:
Khoảng cách từ tâm nửa đường tròn tới bất kỳ điểm nào nằm trên nửa đường tròn đều bằng nhau.
Lời giải chi tiết:
Vì M là vị trí của một điểm thuộc nửa đường tròn quay quanh AB, nên điểm M luôn có cùng khoảng cách từ I đến điểm đó như khoảng cách từ I đến bất kỳ điểm nào trên nửa đường tròn ban đầu, tức là IM = r.
Do bán kính không thay đổi trong suốt quá trình quay, khoảng cách từ I đến M vẫn giữ nguyên giá trị là 𝑟.
Trả lời câu hỏi Luyện tập 1 trang 73 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt cầu (S) đi qua gốc toạ độ O, bán kính r = 5. Tìm toạ độ tâm I của (S), biết điểm I thuộc đường thẳng
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 4 + 2t}\end{array}} \right.\quad (t \in \mathbb{R}).\)
Phương pháp giải:
Gọi \(I(a,b,c)\) là tọa độ của tâm mặt cầu \(S\).
Vì mặt cầu \(S\) đi qua gốc tọa độ \(O(0,0,0)\), nên \(IO = r = 5\).
Đặt \(I\) nằm trên đường thẳng \(d\) và tìm giá trị \(t\) sao cho khoảng cách \(IO = 5\).
Giải phương trình để tìm \(t\), từ đó xác định tọa độ của \(I\).
Lời giải chi tiết:
Giả sử \(I(a,b,c)\) có tọa độ: \(a = 3 - t, b = t, c = 4 + 2t.\)
Do \(IO = 5\), ta có: \(IO = \sqrt {{a^2} + {b^2} + {c^2}} = 5.\)
Thay \(a = 3 - t\), \(b = t\), \(c = 4 + 2t\) vào phương trình:
\(\begin{array}{l}\sqrt {{{(3 - t)}^2} + {t^2} + {{(4 + 2t)}^2}} = 5.\\ \Leftrightarrow 9 - 6t + {t^2} + {t^2} + 16 + 16t + 4{t^2} = 25\\ \Leftrightarrow 6{t^2} + 10t + 25 = 25\\ \Leftrightarrow 2t(3t + 5) = 0\\ \Leftrightarrow t = 0,\,\,\,t = - \frac{5}{3}\end{array}\)
Vậy có hai toạ độ tâm I thoả mãn là \(I(3;0;4)\) hoặc \(I\left( {\frac{{14}}{3}; - \frac{5}{3};\frac{2}{3}} \right)\).
Mục 1 của SGK Toán 12 tập 2 thường xoay quanh các chủ đề về số phức, bao gồm các phép toán cơ bản, biểu diễn hình học của số phức, và các ứng dụng của số phức trong giải toán. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các phần tiếp theo của chương trình.
Bài tập này yêu cầu học sinh thực hiện các phép toán cơ bản trên số phức. Để giải quyết, cần nhớ rõ các quy tắc:
Ví dụ: Tính (2 + 3i) + (1 - i). Giải: (2 + 3i) + (1 - i) = (2 + 1) + (3 - 1)i = 3 + 2i
Số phức z = a + bi được biểu diễn bằng điểm M(a, b) trên mặt phẳng tọa độ. Trục hoành là trục thực, trục tung là trục ảo. Các phép toán trên số phức cũng có thể được biểu diễn bằng các phép biến hình trên mặt phẳng.
Ví dụ: Biểu diễn số phức z = -1 + 2i trên mặt phẳng tọa độ. Giải: Số phức z = -1 + 2i được biểu diễn bằng điểm M(-1, 2).
Cho số phức z = a + bi, phần thực của z là a, phần ảo của z là b. Bài tập này thường yêu cầu học sinh biến đổi số phức về dạng a + bi để xác định phần thực và phần ảo.
Ví dụ: Tìm phần thực và phần ảo của số phức z = (1 + i) / (1 - i). Giải: z = (1 + i) / (1 - i) = [(1 + i)(1 + i)] / [(1 - i)(1 + i)] = (1 + 2i - 1) / (1 + 1) = i. Vậy phần thực của z là 0, phần ảo của z là 1.
Số phức không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực như:
Để củng cố kiến thức và kỹ năng giải bài tập, các em nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Giaitoan.edu.vn cung cấp nhiều bài tập và lời giải chi tiết để các em tham khảo.
Hy vọng với bài giải chi tiết này, các em đã hiểu rõ hơn về các bài tập trong mục 1 trang 72, 73 SGK Toán 12 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!