Chào mừng các em học sinh đến với bài giải bài tập 2.5 trang 65 SGK Toán 12 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán về đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm các tam giác ABC và A'B'C'. O là giao điểm của hai đường thẳng AB' và A'B. a) Chứng minh rằng các đường thẳng GO và CG' song song với nhau. b) Tính độ dài của \(\overrightarrow {GO} \)trong trường hợp ABC.A'B'C' là hình lăng trụ đứng, cạnh bên AA' = 3 và đáy là tam giác đều có cạnh bằng 2.
Đề bài
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm các tam giác ABC và A'B'C'. O là giao điểm của hai đường thẳng AB' và A'B.
a) Chứng minh rằng các đường thẳng GO và CG' song song với nhau.
b) Tính độ dài của \(\overrightarrow {GO} \)trong trường hợp ABC.A'B'C' là hình lăng trụ đứng, cạnh bên AA' = 3 và đáy là tam giác đều có cạnh bằng 2.
Phương pháp giải - Xem chi tiết
- Tìm k (k≠0) sao cho \(\overrightarrow {GO} = k\overrightarrow {CG'} \) thì hai đường thẳng GO // CG’ bằng quy tắc trọng tâm tam giác và quy tắc trung điểm của vectơ.
- Tính độ dài của \(\overrightarrow {CG'} \) rồi suy ra độ dài của \(\overrightarrow {GO} \).
Lời giải chi tiết
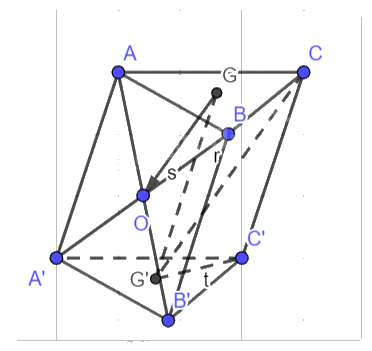
Hình bình hành AA’B’B có O là giao điểm của hai đường chéo nên O là trung điểm của AB’. Do đó: \(2\overrightarrow {GO} = \overrightarrow {GA} + \overrightarrow {GB'} = \overrightarrow {GA} + \overrightarrow {GG'} + \overrightarrow {G'B'} \).
Vì ABC.A’B’C’ là hình lăng trụ có G, G’ lần lượt là trọng tâm của hai đáy nên: \(\overrightarrow {G'B'} = \overrightarrow {GB} ,\overrightarrow {GG'} = \overrightarrow {CC'} ,\overrightarrow {G'C'} = \overrightarrow {GC} \).
Suy ra: \(2\overrightarrow {GO} = \overrightarrow {GA} + \overrightarrow {CC'} + \overrightarrow {GB} = \overrightarrow {GA} + \overrightarrow {CG'} + \overrightarrow {G'C'} + \overrightarrow {GB} = \overrightarrow {GA} + \overrightarrow {CG'} + \overrightarrow {GC} + \overrightarrow {GB} \).
Áp dụng quy tắc trọng tâm của vectơ vào tam giác ABC, ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
Suy ra: \(2\overrightarrow {GO} = \left( {\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GB} } \right) + \overrightarrow {CG'} = \overrightarrow 0 + \overrightarrow {CG'} = \overrightarrow {CG'} \).
Vì tồn tại \(k = \frac{1}{2} \ne 0\) nên GO và CG’ song song với nhau.
b)
Vì ABC.A’B’C’ là hình lăng trụ là lăng trụ đứng nên tam giác CC’G’ vuông tại C’, ta có: \(CG' = \sqrt {CC{'^2} + C'G{'^2}} \).
Mà G’ là trọng tâm của tam giác đều A’B’C’ nên: \(C'G' = \frac{2}{3}.\frac{{\sqrt 3 }}{2}.2 = \frac{{2\sqrt 3 }}{3}\).
Suy ra: \(CG' = \sqrt {{3^2} + {{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}} = \frac{{\sqrt {93} }}{3}\).
Từ câu a ta thấy \(\overrightarrow {GO} = \frac{1}{2}\overrightarrow {CG'} \) nên \(\left| {\overrightarrow {GO} } \right| = \frac{1}{2}\left| {\overrightarrow {CG'} } \right| = \frac{1}{2}.\frac{{\sqrt {93} }}{3} = \frac{{\sqrt {93} }}{6}\).
Bài tập 2.5 trang 65 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Cụ thể, bài tập thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, tìm cực trị và ứng dụng đạo hàm để giải các bài toán tối ưu hóa.
Bài tập 2.5 thường bao gồm các dạng bài sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 2.5 trang 65 SGK Toán 12 tập 1, chúng tôi xin trình bày lời giải chi tiết cho từng bài tập:
Đề bài: (Ví dụ về đề bài)
Lời giải: (Ví dụ về lời giải chi tiết, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Ví dụ về lời giải chi tiết, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận)
Để giải bài tập 2.5 trang 65 SGK Toán 12 tập 1 một cách hiệu quả, các em cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 12:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ giải quyết thành công bài tập 2.5 trang 65 SGK Toán 12 tập 1 và nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm. Chúc các em học tập tốt!