Chào mừng bạn đến với bài học về Lý thuyết Vecto trong không gian Toán 12 trên giaitoan.edu.vn. Đây là một phần kiến thức quan trọng trong chương trình Hình học không gian, giúp bạn giải quyết các bài toán phức tạp và hiểu sâu hơn về không gian ba chiều.
Chúng tôi sẽ cung cấp cho bạn một cách tiếp cận toàn diện, từ định nghĩa cơ bản đến các ứng dụng thực tế, đảm bảo bạn nắm vững kiến thức một cách dễ dàng và hiệu quả.
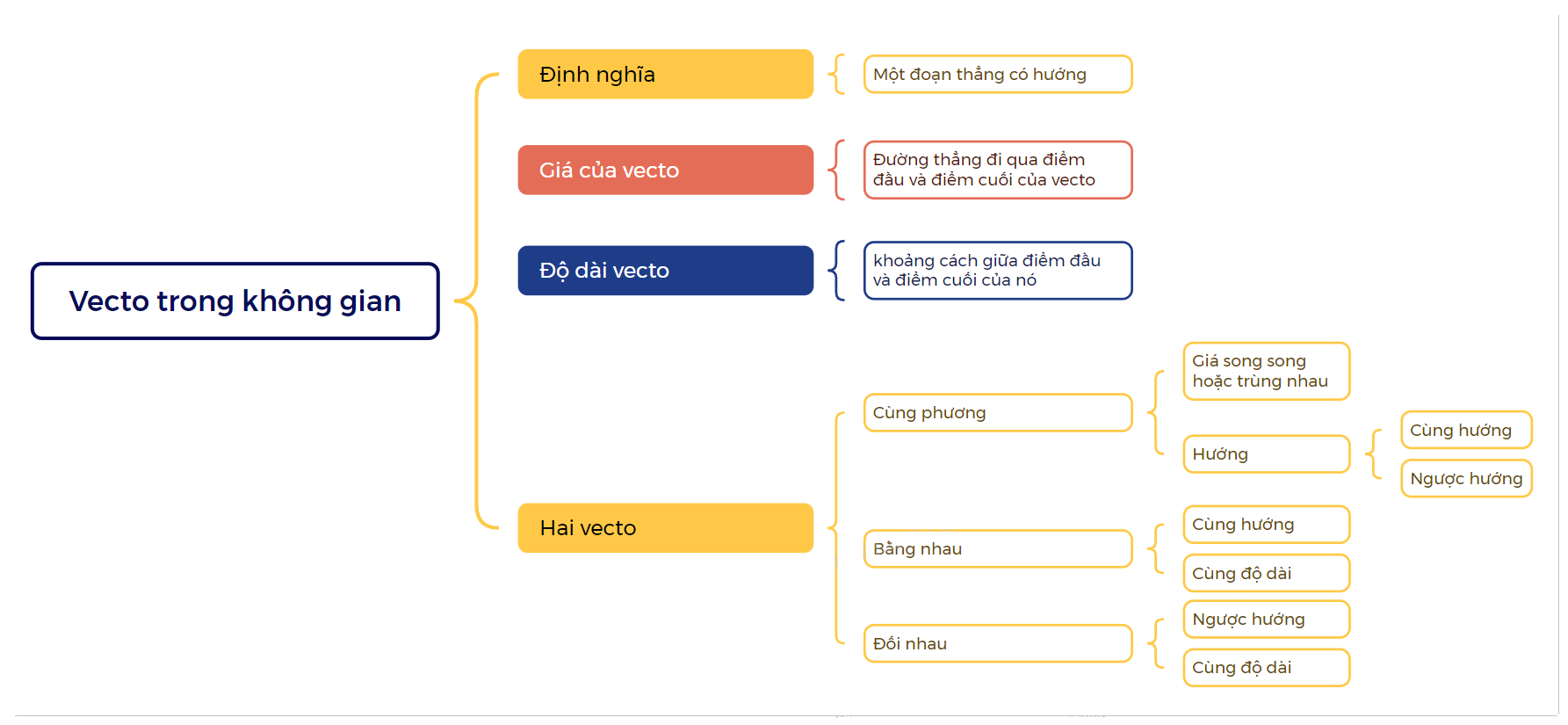
1. Vecto trong không gian
1. Vecto trong không gian
| Vecto trong không gian là một đoạn thẳng có hướng. |
Ví dụ: Cho tứ diện ABCD. Hãy chỉ ra các vecto có điểm đầu A và điểm cuối là một trong các đỉnh còn lại của tứ diện.
Lời giải:
Ngoài đỉnh A, tứ diện còn có 3 đỉnh B, C, D nên ta có 3 vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \).
2. Độ dài của vecto. Hai vecto cùng phương, cùng hướng, bằng nhau
- Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vecto \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\). - Giá của vecto là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó. - Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. - Nếu hai vecto cùng phương thì chúng có thể cùng hướng hoặc ngược hướng. - Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. - Nếu hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng nhau thì ta viết \(\overrightarrow a = \overrightarrow b \).. - Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. - Vecto đối của \(\overrightarrow a \) được kí hiệu là \( - \overrightarrow a \). |
Trong chương trình Toán 12, phần Hình học không gian đóng vai trò quan trọng, và Lý thuyết Vecto trong không gian là nền tảng để giải quyết các bài toán liên quan đến vị trí tương đối của đường thẳng và mặt phẳng, khoảng cách, góc, và nhiều vấn đề khác. Bài viết này sẽ cung cấp một cái nhìn chi tiết về lý thuyết này, bao gồm định nghĩa, các phép toán trên vector, và ứng dụng của chúng.
Một vecto trong không gian là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Ký hiệu: AB, a. Vecto được biểu diễn bằng tọa độ: a = (x; y; z), trong đó x, y, z là các số thực.
Cho hai vecto a = (x1; y1; z1) và b = (x2; y2; z2). Tổng của hai vecto là: a + b = (x1 + x2; y1 + y2; z1 + z2)
Cho hai vecto a = (x1; y1; z1) và b = (x2; y2; z2). Hiệu của hai vecto là: a - b = (x1 - x2; y1 - y2; z1 - z2)
Cho vecto a = (x; y; z) và số thực k. Tích của vecto a với số thực k là: ka = (kx; ky; kz)
Tích vô hướng của hai vecto a = (x1; y1; z1) và b = (x2; y2; z2) là một số thực, được tính bằng công thức: a.b = x1x2 + y1y2 + z1z2
Ứng dụng của tích vô hướng:
Tích có hướng của hai vecto a = (x1; y1; z1) và b = (x2; y2; z2) là một vecto c = [a; b], được tính bằng công thức:
c = (y1z2 - z1y2; z1x2 - x1z2; x1y2 - y1x2)
Ứng dụng của tích có hướng:
Bài 1: Cho a = (1; 2; 3) và b = (-2; 1; 0). Tính a + b, a - b, 2a và a.b.
Giải:
Lý thuyết Vecto trong không gian Toán 12 là một phần kiến thức quan trọng và có nhiều ứng dụng trong thực tế. Việc nắm vững các định nghĩa, phép toán và ứng dụng của vecto sẽ giúp bạn giải quyết các bài toán Hình học không gian một cách hiệu quả và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập.