Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất hàm số Toán 12

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12

Chào mừng bạn đến với bài học về lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trong chương trình Toán 12. Đây là một chủ đề quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia và các bài kiểm tra.

Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về cách xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số, các phương pháp giải bài tập liên quan, và những lưu ý quan trọng để đạt kết quả tốt nhất.

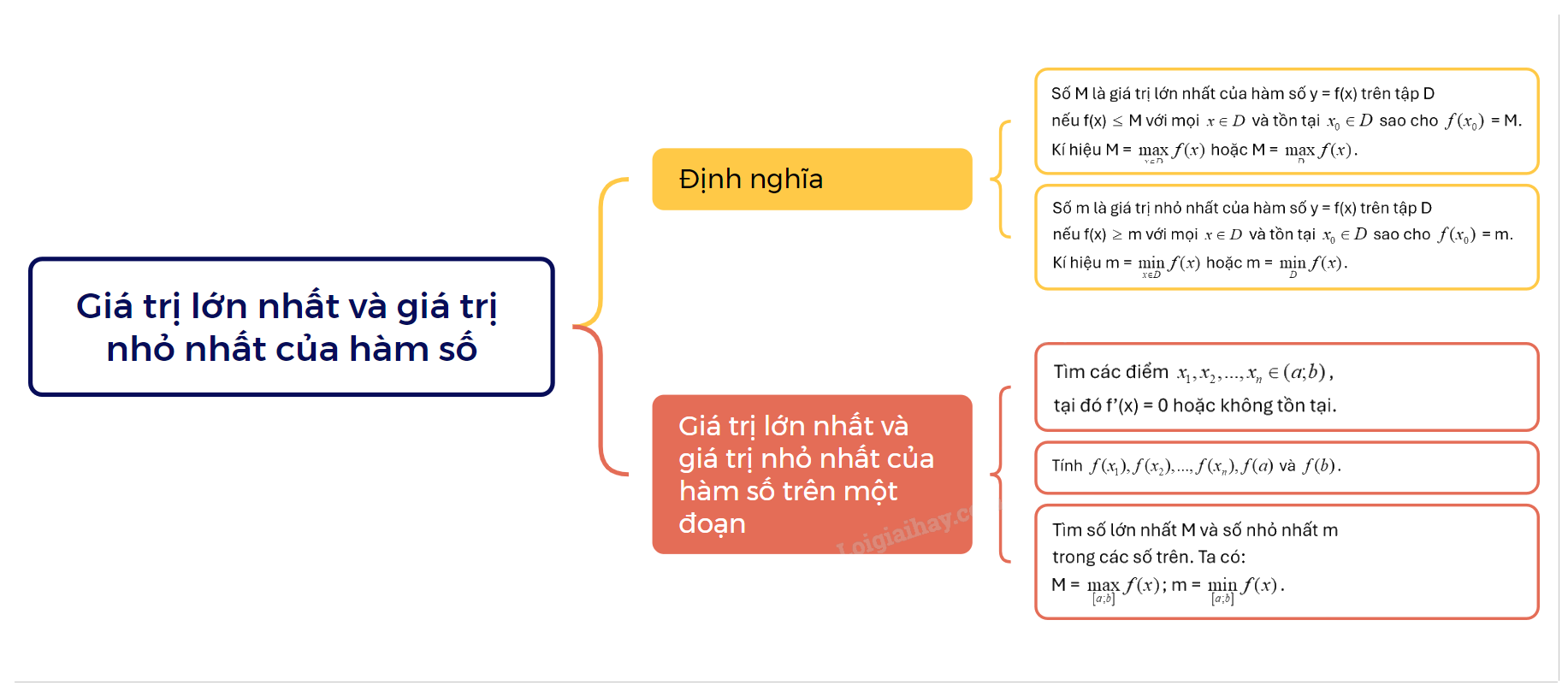
1. Định nghĩa

1. Định nghĩa

Cho hàm số y = f(x) xác định trên tập D.

+) Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) \( \le \) M với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = M. Kí hiệu M = \(\mathop {\max }\limits_{x \in D} f(x)\) hoặc M = \(\mathop {\max }\limits_D f(x)\).

+) Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) \( \ge \) m với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = m. Kí hiệu m = \(\mathop {\min }\limits_{x \in D} f(x)\) hoặc m = \(\mathop {\min }\limits_D f(x)\).

Ví dụ: Tìm GTLN, GTNN của hàm số \(y = f(x) = \sqrt {1 - {x^2}} \).

Tập xác định của hàm số là \(\left[ { - 1;1} \right]\).

Ta có:

\(f(x) = \sqrt {1 - {x^2}} \) \( \ge \) 0; dấu bằng xảy ra khi \(1 - {x^2} = 0\), tức x = -1 hoặc x = 1.

Do đó \(\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0\).

\(f(x) = \sqrt {1 - {x^2}} \) \( \le 1\); dấu bằng xảy ra khi \(1 - {x^2} = 1\), tức x = 0.

Do đó \(\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1\).

2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\):

Tìm các điểm \({x_1},{x_2},...,{x_n} \in (a;b)\), tại đó f’(x) = 0 hoặc không tồn tại.
Tính \(f({x_1}),f({x_2}),...,f({x_n}),f(a)\) và \(f(b)\).
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
M = \(\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)\); m = \(\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)\).

Ví dụ: Tìm GTLN và GTNN của hàm số \(y = {x^4} - 4{x^2} + 3\) trên đoạn \(\left[ {0;4} \right]\).

Ta có: \(y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0\) hoặc \(x = \sqrt 2 \) (vì \(x \in \left[ {0;4} \right]\)).

y(0) = 3; y(4) = 195; y(\(\sqrt 2 \)) = -1.

Do đó: \(\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195\); \(\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1\).

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá 1

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá đặc sắc thuộc chuyên mục đề thi toán 12 trên nền tảng đề thi toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12

Trong chương trình Toán 12, việc nắm vững lý thuyết về giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số là vô cùng quan trọng. Nó không chỉ giúp học sinh hiểu sâu hơn về tính chất của hàm số mà còn là nền tảng để giải quyết các bài toán thực tế và các bài toán trong kỳ thi THPT Quốc gia.

1. Khái niệm cơ bản

Giá trị lớn nhất của hàm số f(x) trên một khoảng hoặc tập xác định D là giá trị M sao cho f(x) ≤ M với mọi x thuộc D và tồn tại x₀ thuộc D sao cho f(x₀) = M. Tương tự, giá trị nhỏ nhất của hàm số f(x) trên D là giá trị m sao cho f(x) ≥ m với mọi x thuộc D và tồn tại x₀ thuộc D sao cho f(x₀) = m.

2. Các phương pháp tìm GTLN và GTNN

Có nhiều phương pháp để tìm GTLN và GTNN của hàm số, tùy thuộc vào dạng hàm số và khoảng xác định. Dưới đây là một số phương pháp phổ biến:

Phương pháp đại số: Sử dụng các bất đẳng thức, biến đổi tương đương để tìm GTLN và GTNN.
Phương pháp sử dụng đạo hàm: Tìm các điểm cực trị của hàm số, sau đó so sánh giá trị của hàm số tại các điểm cực trị và các điểm biên của khoảng xác định để tìm GTLN và GTNN.
Phương pháp hình học: Vẽ đồ thị hàm số và xác định GTLN và GTNN từ đồ thị.

3. Ứng dụng của việc tìm GTLN và GTNN

Việc tìm GTLN và GTNN của hàm số có nhiều ứng dụng trong thực tế, ví dụ như:

Bài toán tối ưu hóa: Tìm kích thước tối ưu của một vật thể để đạt được hiệu quả cao nhất.
Bài toán kinh tế: Tìm mức sản lượng tối ưu để đạt được lợi nhuận cao nhất.
Bài toán vật lý: Tìm vận tốc tối đa hoặc gia tốc tối đa của một vật thể.

4. Ví dụ minh họa

Ví dụ 1: Tìm GTLN và GTNN của hàm số f(x) = x² - 4x + 3 trên khoảng [-1; 3].

Giải:

Tính đạo hàm: f'(x) = 2x - 4
Tìm điểm cực trị: f'(x) = 0 => x = 2
Tính giá trị của hàm số tại các điểm cực trị và điểm biên:

f(-1) = (-1)² - 4(-1) + 3 = 8
f(2) = 2² - 4(2) + 3 = -1
f(3) = 3² - 4(3) + 3 = 0

Kết luận: GTLN của hàm số là 8 tại x = -1, GTNN của hàm số là -1 tại x = 2.

Ví dụ 2: Tìm GTLN của hàm số f(x) = -x² + 6x - 5 trên khoảng (0; 5).

Giải:

Hàm số f(x) là hàm bậc hai với hệ số a = -1 < 0, nên hàm số đạt GTLN tại đỉnh của parabol. Hoành độ đỉnh là x = -b/(2a) = -6/(2*(-1)) = 3. Giá trị GTLN là f(3) = -3² + 6*3 - 5 = 4.

5. Lưu ý khi giải bài toán GTLN và GTNN

Xác định đúng khoảng xác định của hàm số.
Sử dụng phương pháp phù hợp với từng dạng hàm số.
Kiểm tra kỹ các điều kiện của bài toán.
So sánh giá trị của hàm số tại các điểm cực trị và điểm biên để tìm GTLN và GTNN.

Hy vọng bài học này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!