Chào mừng các em học sinh đến với bài giải bài tập 3.15 trang 106 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Hai bảng dưới đây biểu diễn kết quả đo đường kính (tính theo mm) của một số ổ bi được sản xuất bởi các máy X và Y:
Đề bài
Hai bảng dưới đây biểu diễn kết quả đo đường kính (tính theo mm) của một số ổ bi được sản xuất bởi các máy X và Y:
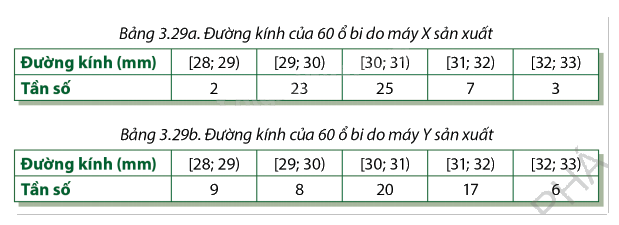
a) Ước tính giá trị trung bình và độ lệch chuẩn của đường kính các ổ bi được sản xuất bởi mỗi máy.
b) Biết rằng đường kính mong muốn cho các ổ bi là 30,4 mm. Hãy phân tích chất lượng sản phẩm do mỗi máy sản xuất.
Phương pháp giải - Xem chi tiết
a) Áp dụng các công thức sau:
- Công thức tính trung bình:
\(\bar x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\bar x} \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\bar x} \right)}^2}} \)
b) So sánh giá trị trung bình và độ lệch chuẩn với giá trị mong muốn (30,4 mm) để đánh giá sự chính xác và độ phân tán của sản phẩm.
Lời giải chi tiết
Bảng phân phối tần số cho máy X và Y:
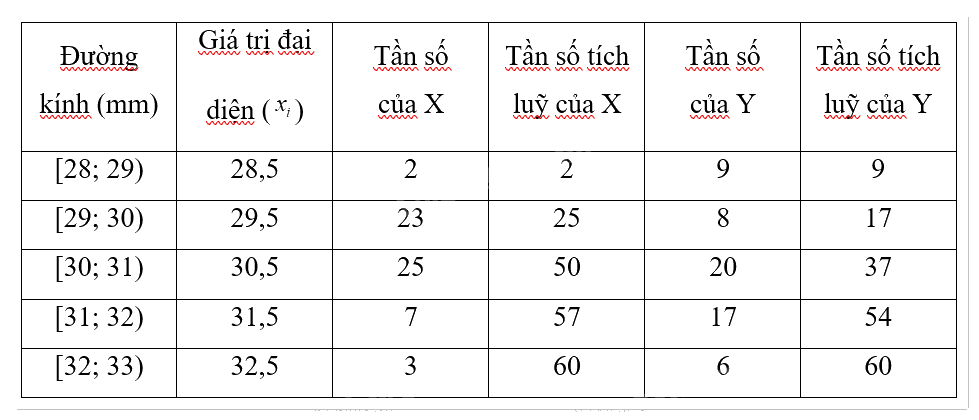
Dựa vào bảng phân phối ta thấy N = 60.
Giá trị trung bình của máy X:
\({\bar x_X} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{2 \times 28,5 + 23 \times 29,5 + 25 \times 30,5 + 7 \times 31,5 + 3 \times 32,5}}{{60}} = \frac{{1816}}{{60}} \approx 30,27\)
Độ lệch chuẩn của máy X:
\({S_X} = \sqrt {\overline {x_X^2} - {{\left( {{{\bar x}_X}} \right)}^2}} \)
\(\overline {x_X^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{2 \times 28,{5^2} + 23 \times 29,{5^2} + 25 \times 30,{5^2} + 7 \times 31,{5^2} + 3 \times 32,{5^2}}}{{60}} = \frac{{55011}}{{60}} = 916,85\)
\({S_X} = \sqrt {916,85 - 30,{{27}^2}} = \sqrt {0,78} \approx 0,88\)
Giá trị trung bình của máy Y:
\({\bar x_Y} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{9 \times 28,5 + 8 \times 29,5 + 20 \times 30,5 + 17 \times 31,5 + 6 \times 32,5}}{{60}} = \frac{{1833}}{{60}} = 30,55\)
Độ lệch chuẩn của phương pháp B:
\({S_Y} = \sqrt {\overline {x_Y^2} - {{\left( {{{\bar x}_Y}} \right)}^2}} \)
\(\overline {x_Y^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{9 \times 28,{5^2} + 8 \times 29,{5^2} + 20 \times 30,{5^2} + 17 \times 31,{5^2} + 6 \times 32,{5^2}}}{{60}} = \frac{{56083}}{{60}} \approx 934,72\)
\({S_Y} = \sqrt {934,72 - 30,{{55}^2}} = \sqrt {1,4175} \approx 1,19\)
b)
Phân tích chất lượng sản phẩm:
- Máy X: Như đã tính trước đó, giá trị trung bình là 30.27 mm và độ lệch chuẩn là 0.88 mm.
- Máy Y: Với giá trị trung bình mới là 30.55 mm và độ lệch chuẩn là 1.19 mm.
Kết luận:
- Máy X sản xuất sản phẩm có đường kính trung bình gần với giá trị mong muốn hơn (30,27 mm so với 30,4 mm), với độ lệch chuẩn nhỏ hơn, cho thấy sản phẩm đều hơn.
- Máy Y có giá trị trung bình lớn hơn 30,4 mm (30,55 mm), và độ lệch chuẩn cũng lớn hơn, cho thấy sản phẩm có sự biến thiên lớn hơn về kích thước, chất lượng không đồng đều bằng sản phẩm của máy X.
Do đó, sản phẩm của máy X vẫn được đánh giá là có chất lượng tốt hơn so với máy Y.
Bài tập 3.15 trang 106 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết một bài toán thực tế liên quan đến tối ưu hóa. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài tập 3.15 yêu cầu tìm giá trị lớn nhất của diện tích hình chữ nhật có chu vi bằng 20cm. Ta có thể giải bài tập này như sau:
Lưu ý quan trọng:
Trong quá trình giải bài tập, cần chú ý các điểm sau:
Các dạng bài tập tương tự:
Ngoài bài tập 3.15, các em có thể gặp các dạng bài tập tương tự như:
Tài liệu tham khảo:
Hy vọng với bài giải chi tiết này, các em sẽ hiểu rõ hơn về phương pháp giải bài tập 3.15 trang 106 SGK Toán 12 tập 1 và tự tin hơn trong quá trình học tập. Chúc các em học tốt!
| Công thức đạo hàm cơ bản | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x2)' = 2x |
| (sin x)' = cos x | (sin 2x)' = 2cos 2x |
| (cos x)' = -sin x | (cos 3x)' = -3sin 3x |