Chào mừng các em học sinh đến với bài giải bài tập 4.19 trang 31 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Tính diện tích hình phẳng được gạch chép trong Hình 4.26.
Đề bài
Tính diện tích hình phẳng được gạch chép trong Hình 4.26.
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hai số \(y = f(x)\), \(y = g(x)\) và các đường thẳng \(x = a\), \(x = b\):
\(S = \int_a^b {\left| {f(x) - g(x)} \right|} dx\).
Lời giải chi tiết
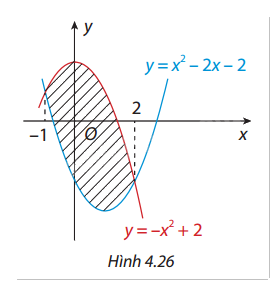
Nhìn vào Hình 4.26 ta nhận thấy hình phẳng được giới hạn hai đồ thị hàm số là \(y = {x^2} - 2x - 2\) và \(y = - {x^2} + 2\) và hai đường thẳng là \(x = - 1\), \(x = 2\).
Diện tích hình phẳng là:
\(S = \int_{ - 1}^2 {\left| {({x^2} - 2x - 2) - ( - {x^2} + 2)} \right|dx} = \int_{ - 1}^2 {\left| {2{x^2} - 2x - 4} \right|dx} \)
Biểu thức \(2{x^2} - 2x - 4\) âm trên \(( - 1,2)\), nên:
\(S = - \int_{ - 1}^2 {(2{x^2} - 2x - 4)dx} \)
\(\int {(2{x^2} - 2x - 4)} dx = \frac{2}{3}{x^3} - {x^2} - 4x\)
\(S = - \left[ {\left( {\frac{2}{3}({2^3}) - ({2^2}) - 4(2)} \right) - \left( {\frac{2}{3}{{( - 1)}^3} - {{( - 1)}^2} - 4( - 1)} \right)} \right] = - \left( { - \frac{{20}}{3} - \frac{7}{3}} \right) = 9\).
Bài tập 4.19 trang 31 SGK Toán 12 tập 2 yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số. Cụ thể, bài toán thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị của hàm số, và cuối cùng là vẽ đồ thị hàm số.
Để giải bài tập 4.19 trang 31 SGK Toán 12 tập 2 một cách hiệu quả, học sinh cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là: y = x3 - 3x2 + 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | ĐB | NB |
Ngoài bài tập 4.19, SGK Toán 12 tập 2 còn nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về đạo hàm. Một số dạng bài tập thường gặp bao gồm:
Mẹo giải:
Để học tốt môn Toán 12, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 4.19 trang 31 SGK Toán 12 tập 2. Chúc các em học tập tốt!