Chào mừng các em học sinh đến với bài giải bài tập 1.20 trang 34 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến kiến thức đã học.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin hơn trong quá trình học tập.
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: a) (y = {x^3} + 3{x^2} - 4) b) (y = {x^3} + 4{x^2} + 4x) c) (y = - 2{x^3} + 2) d) (y = - {x^3} - {x^2} - x + 1)
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = {x^3} + 3{x^2} - 4\)
b) \(y = {x^3} + 4{x^2} + 4x\)
c) \(y = - 2{x^3} + 2\)
d) \(y = - {x^3} - {x^2} - x + 1\)
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
Lời giải chi tiết
a)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} - 4} \right) = \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3{x^2} - 4} \right) = - \infty \)
Ta có: \({y^\prime } = 3{x^2} + 6x\)
\({y^\prime } = 0 \leftrightarrow 3{x^2} + 6x = 0 \leftrightarrow x = - 2{\rm{ hoac }}x = 0\)
Bảng biến thiên:
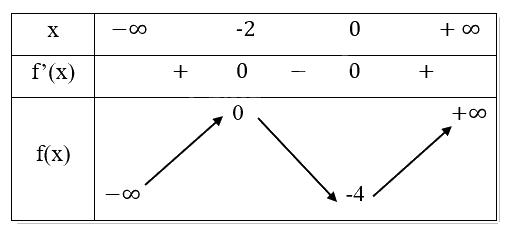
Chiều biến thiên: Hàm số đồng biến trên các khoảng (−∞,-2) và (0,∞), nghịch biến trên khoảng (-2,0).
Cực trị: Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} = - 4\)
Hàm số đạt cực đại tại \(x = - 2,{y_{CD}} = 0\)
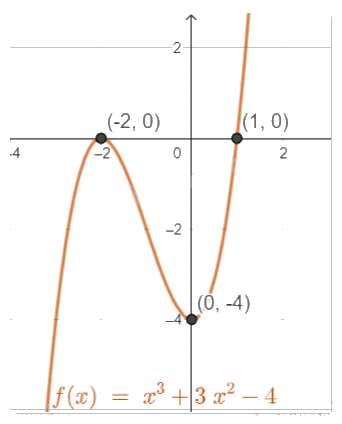
- Vẽ đồ thị:
Giao điểm với trục Oy là (0,-4).
Giao điểm với trục Ox là (-2,0), (1,0).
b)
- Tập xác định: D = R.
- Sự biến thiên:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 4{x^2} + 4x} \right) = \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 4{x^2} + 4x} \right) = - \infty \)
Ta có: \({y^\prime } = 3{x^2} + 8x + 4\)
\({y^\prime } = 0 \leftrightarrow 3{x^2} + 8x + 4 = 0 \leftrightarrow x = - 2{\rm{ }}\)hoặc \(x = \frac{{ - 2}}{3}\)
Bảng biến thiên:
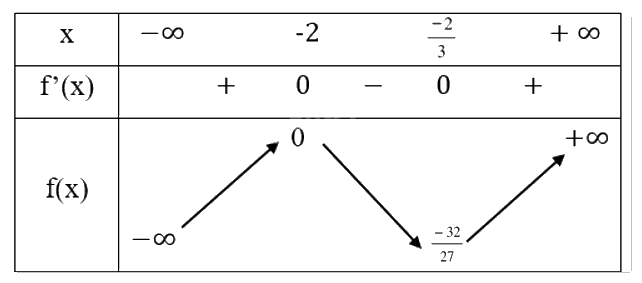
Chiều biến thiên: Hàm số đồng biến trên các khoảng \(( - \infty , - 2)\) và \(\left( {\frac{{ - 2}}{3},\infty } \right)\), nghịch biến trên khoảng \(\left( { - 2,\frac{{ - 2}}{3}} \right)\).
Cực trị: Hàm số đạt cực tiểu tại \(x = \frac{{ - 2}}{3},{y_{CT}} = - \frac{{32}}{{27}}\)
Hàm số đạt cực đại tại \(x = - 2,{y_{CD}} = 0\)
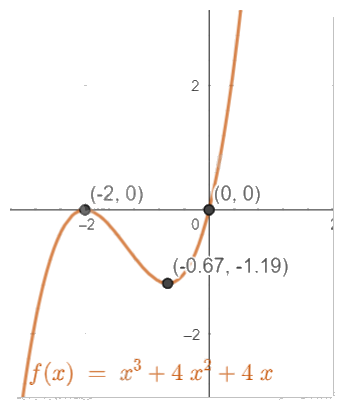
- Vẽ đồ thị:
Đi qua gốc tọa độ O(0,0).
Giao điểm với trục Ox là (-2,0).
c)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 2} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y{\rm{ }} = \mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 2} \right) = \infty \)
Ta có: \({y^\prime } = - 6{x^2} \le 0\forall x \in R\)
\({y^\prime } = 0 \leftrightarrow - 6x = 0 \leftrightarrow x = 0{\rm{ }}\)
Bảng biến thiên:
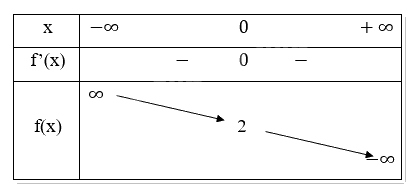
Chiều biến thiên: Hàm số nghịch biến trên R.
Cực trị: Hàm số không có cực trị
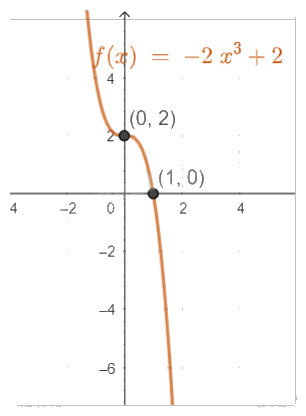
- Vẽ đồ thị:
Giao điểm với trục Oy là (0,2).
Giao điểm với trục Ox là (1,0).
d) \(\)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} - {x^2} - x + 1} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y{\rm{ }} = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} - {x^2} - x + 1} \right) = \infty \)
Ta có: \({y^\prime } = - 3{x^2} - 2x - 1 < 0\forall x \in R\)
Bảng biến thiên:
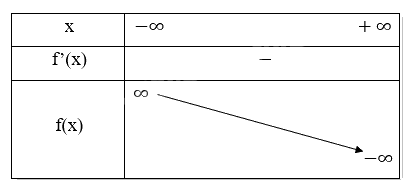
Chiều biến thiên: Hàm số nghịch biến trên R.
Cực trị: Hàm số không có cực trị
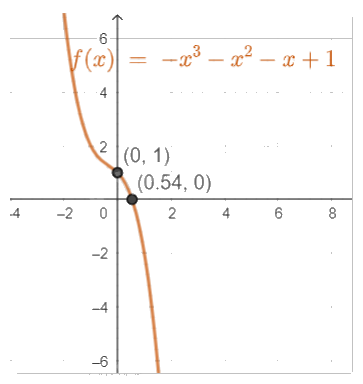
- Vẽ đồ thị
Giao với trục Oy tại điểm (0,1)
Giao với trục Ox tại điểm (0.5437,0)
Bài tập 1.20 trang 34 SGK Toán 12 tập 1 thường xoay quanh các chủ đề như đường thẳng trong không gian, mặt phẳng trong không gian, quan hệ song song, quan hệ vuông góc. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức cơ bản:
Để giải bài tập 1.20 trang 34 SGK Toán 12 tập 1, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lựa chọn phương pháp giải phù hợp. Thông thường, bài toán sẽ yêu cầu:
Giả sử bài tập 1.20 yêu cầu: Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Hãy viết phương trình đường thẳng AB.
Lời giải:
Ngoài bài tập 1.20, SGK Toán 12 tập 1 còn nhiều bài tập tương tự. Để giải tốt các bài tập này, học sinh cần:
Kiến thức về đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, đồ họa máy tính và vật lý.
Hy vọng với lời giải chi tiết và phương pháp tiếp cận bài tập 1.20 trang 34 SGK Toán 12 tập 1 này, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán.