Chào mừng các em học sinh đến với bài giải chi tiết mục 4 trang 50, 51 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài học này tập trung vào các kiến thức quan trọng của chương trình Toán 12, đặc biệt là các dạng bài tập thường gặp trong các kỳ thi. Hãy cùng chúng tôi khám phá và chinh phục những thử thách này nhé!
Trong không gian Oxyz, cho mặt phẳng \((\alpha ):Ax + By + Cz + D = 0\) có vectơ pháp tuyến \(\vec n = (A;B;C)\) và điểm \({M_0}({x_0};{y_0};{z_0})\). Gọi \({M_1}({x_1};{y_1};{z_1})\) là hình chiếu vuông góc của \({M_0}\) trên \((\alpha )\) (Hình 5.13). a) Tính \(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right|\) theo \(A,B,C,D,{x_0},{y_0},{z_0}\). b) Giải thích tại sao ta có \(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \ri
Trả lời câu hỏi Luyện tập 10 trang 51 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính khoảng cách:
a) Từ điểm \(A( - 3; - 2; - 5)\) đến mặt phẳng \((\alpha ):2x - 2y + z - 5 = 0\);
b) Giữa hai mặt phẳng \((\alpha ):y - 4 = 0\) và \((\beta ):y + 5 = 0\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách từ một điểm tới mặt phẳng:
\(d = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)
b) Khoảng cách giữa hai mặt phẳng song song được tính bằng công thức:
\(d = \left| {\frac{{{D_1} - {D_2}}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}} \right|\)
Lời giải chi tiết:
a) Khoảng cách từ điểm \(A( - 3; - 2; - 5)\) đến mặt phẳng \(\left( \alpha \right):2x - 2y + z - 5 = 0\) là:
\({d_A} = \frac{{\left| {2.( - 3) - 2.( - 2) + 1.( - 5) - 5} \right|}}{{\sqrt {{2^2} + {{(2)}^2} + {1^2}} }} = \frac{{\left| { - 12} \right|}}{{\sqrt 9 }} = \frac{{12}}{3} = 4\)
b) Có thể thấy hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau nên khoảng cách giữa hai mặt phẳng là:
\(d = \frac{{\left| { - 4 - 5} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} }} = \frac{{\left| { - 9} \right|}}{1} = 9\)
Trả lời câu hỏi Hoạt động 8 trang 50 SGK Toán 12 Cùng khám phá
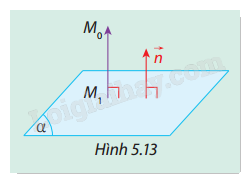
Trong không gian Oxyz, cho mặt phẳng \((\alpha ):Ax + By + Cz + D = 0\) có vectơ pháp tuyến \(\vec n = (A;B;C)\) và điểm \({M_0}({x_0};{y_0};{z_0})\). Gọi \({M_1}({x_1};{y_1};{z_1})\) là hình chiếu vuông góc của \({M_0}\) trên \((\alpha )\) (Hình 5.13).
a) Tính \(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right|\) theo \(A,B,C,D,{x_0},{y_0},{z_0}\).
b) Giải thích tại sao ta có \(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right| \cdot \left| {\vec n} \right|\). Từ đó, tính \(\left| {\overrightarrow {{M_1}{M_0}} } \right|\) theo \(A,B,C,D,{x_0},{y_0},{z_0}\).
Phương pháp giải:
- Sử dụng vectơ pháp tuyến của mặt phẳng để xác định phương của đoạn thẳng từ \({M_0}\) đến hình chiếu \({M_1}\).
- Tính tích vô hướng của vectơ \(\overrightarrow {{M_1}{M_0}} \) và vectơ pháp tuyến \(\vec n\).
- Giải thích mối liên hệ giữa tích vô hướng và độ lớn của các vectơ.
- Từ biểu thức của tích vô hướng và độ lớn của các vectơ, tính được độ dài đoạn thẳng \({M_1}{M_0}\) là khoảng cách từ \({M_0}\) đến mặt phẳng \((\alpha )\).
Lời giải chi tiết:
a)
Mặt phẳng \((\alpha )\) có phương trình tổng quát:
\(Ax + By + Cz + D = 0,\)
trong đó, \(\vec n = (A,B,C)\) là vectơ pháp tuyến của mặt phẳng \((\alpha )\).
\({M_0}({x_0},{y_0},{z_0})\) là điểm nằm ngoài mặt phẳng, và \({M_1}({x_1},{y_1},{z_1})\) là hình chiếu vuông góc của \({M_0}\) lên mặt phẳng \((\alpha )\). Do \({M_1}\) nằm trên mặt phẳng, ta có:
\(A{x_1} + B{y_1} + C{z_1} + D = 0.\)
Vectơ \(\overrightarrow {{M_0}{M_1}} \) nối từ \({M_0}\) đến \({M_1}\) có dạng:
\(\overrightarrow {{M_0}{M_1}} = ({x_1} - {x_0},{y_1} - {y_0},{z_1} - {z_0}).\)
Tích vô hướng của \(\overrightarrow {{M_0}{M_1}} \) và \(\vec n\) được tính là:
\(\overrightarrow {{M_0}{M_1}} \cdot \vec n = A({x_1} - {x_0}) + B({y_1} - {y_0}) + C({z_1} - {z_0}).\)
Khai triển:
\(A({x_1} - {x_0}) + B({y_1} - {y_0}) + C({z_1} - {z_0}) = A{x_1} + B{y_1} + C{z_1} - (A{x_0} + B{y_0} + C{z_0}).\)
Từ phương trình mặt phẳng, ta biết:
\(A{x_1} + B{y_1} + C{z_1} + D = 0\)
do đó:
\(A{x_1} + B{y_1} + C{z_1} = - D.\)
Thay vào phương trình tích vô hướng:
\(\overrightarrow {{M_0}{M_1}} \cdot \vec n = - D - (A{x_0} + B{y_0} + C{z_0}).\)
Vậy ta có:
\(\overrightarrow {{M_0}{M_1}} \cdot \vec n = - (A{x_0} + B{y_0} + C{z_0} + D).\)
Do đó:
\(\left| {\overrightarrow {{M_0}{M_1}} \cdot \vec n} \right| = |A{x_0} + B{y_0} + C{z_0} + D|.\)
b)
Theo định nghĩa của tích vô hướng, ta có:
\(\overrightarrow {{M_1}{M_0}} \cdot \vec n = \left| {\overrightarrow {{M_1}{M_0}} } \right| \cdot \left| {\vec n} \right| \cdot \cos \theta ,\)
với \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\). Do \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) song song với nhau, nên \(\theta = {0^\circ }\), và \(\cos {0^\circ } = 1\). Do đó:
\(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right| \cdot \left| {\vec n} \right|.\)
Suy ra:
\(\left| {{M_1}{M_0}} \right| = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)
Vậy khoảng cách từ điểm \({M_0}({x_0};{y_0};{z_0})\) đến mặt phẳng \((\alpha ):Ax + By + Cz + D = 0\) là:
\(\left| {{M_1}{M_0}} \right| = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)
Trả lời câu hỏi Vận dụng 2 trang 51 SGK Toán 12 Cùng khám phá
Sử dụng phương pháp tọa độ để giải bài toán sau:
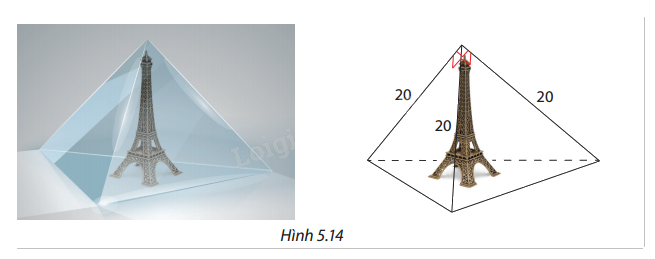
Bạn An muốn trưng bày một mô hình tháp Eiffel trong một cái hộp có dạng hình chóp tam giác đều với cạnh bên bằng 20 cm. Các mặt bên là các tam giác vuông và chân tháp nằm trên mặt đáy của cái hộp (Hình 5.14). Hỏi nếu mô hình tháp Eiffel này cao 11 cm thì có đặt được trong hộp không? Vì sao?
Phương pháp giải:
- Thiết lập hệ tọa độ Oxyz.
- Xác định tọa độ các đỉnh của tam giác đáy.
- Sử dụng định lý Pythagoras để tính chiều cao của hình chóp.
- So sánh chiều cao của mô hình với chiều cao của hình chóp.
- Kết luận mô hình có đặt vừa trong hộp hay không.
Lời giải chi tiết:
Gọi mặt đáy là tam giác ABC. Ta có các cạnh của tam giác ABC sẽ bằng:
\(AB = AC = BC = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,\,(cm)\)
Suy ra đường trung tuyến trong tam giác ABC là:
\(20\sqrt 2 .\frac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,\,(cm)\)
Đặt gốc toạ độ \(O(0;0;0)\) tại trung điểm của của BC, trục Oy trùng với BC, trục Oy nằm trên đường trung tuyến của điểm A. Từ đó suy ra các toạ độ của tam giác như sau:
\(A(10\sqrt 6 ;0;0),\,\,\,\,\,B(0; - 10;0),\,\,\,\,\,\,C(0;10;0)\)
Gọi toạ độ trọng tâm tam giác ABC là G, toạ độ của G là:
\(G\left( {\frac{{10\sqrt 6 }}{3};0;0} \right)\)
Gọi h là chiều cao của hình chóp, ta gọi đỉnh hình chóp là S. Vì hình chóp S.ABC là hình chóp tam giác đều nên toạ độ của S sẽ là: \(\left( {\frac{{10\sqrt 6 }}{3};0;h} \right)\).
Theo đề bài ta có độ dài các cạnh bên là 20cm, tương đương:
\(SA = 20 \Rightarrow \sqrt {{{\left( {10\sqrt 6 - \frac{{10\sqrt 6 }}{3}} \right)}^2} + {h^2}} = 20 = > {h^2} = {20^2} - {\left( {10\sqrt 6 - \frac{{10\sqrt 6 }}{3}} \right)^2}\)
\(h = \sqrt {\frac{{400}}{3}} = \frac{{20}}{{\sqrt 3 }} \approx 11,547\,\,\,(cm)\)
Vì chiều cao của hộp lớn hơn chiều cao của mô hình nên bạn An có thể đặt mô hình tháp Eiffel vào trong hộp.
Trả lời câu hỏi Hoạt động 8 trang 50 SGK Toán 12 Cùng khám phá
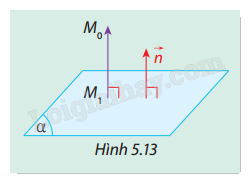
Trong không gian Oxyz, cho mặt phẳng \((\alpha ):Ax + By + Cz + D = 0\) có vectơ pháp tuyến \(\vec n = (A;B;C)\) và điểm \({M_0}({x_0};{y_0};{z_0})\). Gọi \({M_1}({x_1};{y_1};{z_1})\) là hình chiếu vuông góc của \({M_0}\) trên \((\alpha )\) (Hình 5.13).
a) Tính \(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right|\) theo \(A,B,C,D,{x_0},{y_0},{z_0}\).
b) Giải thích tại sao ta có \(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right| \cdot \left| {\vec n} \right|\). Từ đó, tính \(\left| {\overrightarrow {{M_1}{M_0}} } \right|\) theo \(A,B,C,D,{x_0},{y_0},{z_0}\).
Phương pháp giải:
- Sử dụng vectơ pháp tuyến của mặt phẳng để xác định phương của đoạn thẳng từ \({M_0}\) đến hình chiếu \({M_1}\).
- Tính tích vô hướng của vectơ \(\overrightarrow {{M_1}{M_0}} \) và vectơ pháp tuyến \(\vec n\).
- Giải thích mối liên hệ giữa tích vô hướng và độ lớn của các vectơ.
- Từ biểu thức của tích vô hướng và độ lớn của các vectơ, tính được độ dài đoạn thẳng \({M_1}{M_0}\) là khoảng cách từ \({M_0}\) đến mặt phẳng \((\alpha )\).
Lời giải chi tiết:
a)
Mặt phẳng \((\alpha )\) có phương trình tổng quát:
\(Ax + By + Cz + D = 0,\)
trong đó, \(\vec n = (A,B,C)\) là vectơ pháp tuyến của mặt phẳng \((\alpha )\).
\({M_0}({x_0},{y_0},{z_0})\) là điểm nằm ngoài mặt phẳng, và \({M_1}({x_1},{y_1},{z_1})\) là hình chiếu vuông góc của \({M_0}\) lên mặt phẳng \((\alpha )\). Do \({M_1}\) nằm trên mặt phẳng, ta có:
\(A{x_1} + B{y_1} + C{z_1} + D = 0.\)
Vectơ \(\overrightarrow {{M_0}{M_1}} \) nối từ \({M_0}\) đến \({M_1}\) có dạng:
\(\overrightarrow {{M_0}{M_1}} = ({x_1} - {x_0},{y_1} - {y_0},{z_1} - {z_0}).\)
Tích vô hướng của \(\overrightarrow {{M_0}{M_1}} \) và \(\vec n\) được tính là:
\(\overrightarrow {{M_0}{M_1}} \cdot \vec n = A({x_1} - {x_0}) + B({y_1} - {y_0}) + C({z_1} - {z_0}).\)
Khai triển:
\(A({x_1} - {x_0}) + B({y_1} - {y_0}) + C({z_1} - {z_0}) = A{x_1} + B{y_1} + C{z_1} - (A{x_0} + B{y_0} + C{z_0}).\)
Từ phương trình mặt phẳng, ta biết:
\(A{x_1} + B{y_1} + C{z_1} + D = 0\)
do đó:
\(A{x_1} + B{y_1} + C{z_1} = - D.\)
Thay vào phương trình tích vô hướng:
\(\overrightarrow {{M_0}{M_1}} \cdot \vec n = - D - (A{x_0} + B{y_0} + C{z_0}).\)
Vậy ta có:
\(\overrightarrow {{M_0}{M_1}} \cdot \vec n = - (A{x_0} + B{y_0} + C{z_0} + D).\)
Do đó:
\(\left| {\overrightarrow {{M_0}{M_1}} \cdot \vec n} \right| = |A{x_0} + B{y_0} + C{z_0} + D|.\)
b)
Theo định nghĩa của tích vô hướng, ta có:
\(\overrightarrow {{M_1}{M_0}} \cdot \vec n = \left| {\overrightarrow {{M_1}{M_0}} } \right| \cdot \left| {\vec n} \right| \cdot \cos \theta ,\)
với \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\). Do \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) song song với nhau, nên \(\theta = {0^\circ }\), và \(\cos {0^\circ } = 1\). Do đó:
\(\left| {\overrightarrow {{M_1}{M_0}} \cdot \vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right| \cdot \left| {\vec n} \right|.\)
Suy ra:
\(\left| {{M_1}{M_0}} \right| = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)
Vậy khoảng cách từ điểm \({M_0}({x_0};{y_0};{z_0})\) đến mặt phẳng \((\alpha ):Ax + By + Cz + D = 0\) là:
\(\left| {{M_1}{M_0}} \right| = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)
Trả lời câu hỏi Luyện tập 10 trang 51 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính khoảng cách:
a) Từ điểm \(A( - 3; - 2; - 5)\) đến mặt phẳng \((\alpha ):2x - 2y + z - 5 = 0\);
b) Giữa hai mặt phẳng \((\alpha ):y - 4 = 0\) và \((\beta ):y + 5 = 0\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách từ một điểm tới mặt phẳng:
\(d = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)
b) Khoảng cách giữa hai mặt phẳng song song được tính bằng công thức:
\(d = \left| {\frac{{{D_1} - {D_2}}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}} \right|\)
Lời giải chi tiết:
a) Khoảng cách từ điểm \(A( - 3; - 2; - 5)\) đến mặt phẳng \(\left( \alpha \right):2x - 2y + z - 5 = 0\) là:
\({d_A} = \frac{{\left| {2.( - 3) - 2.( - 2) + 1.( - 5) - 5} \right|}}{{\sqrt {{2^2} + {{(2)}^2} + {1^2}} }} = \frac{{\left| { - 12} \right|}}{{\sqrt 9 }} = \frac{{12}}{3} = 4\)
b) Có thể thấy hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau nên khoảng cách giữa hai mặt phẳng là:
\(d = \frac{{\left| { - 4 - 5} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} }} = \frac{{\left| { - 9} \right|}}{1} = 9\)
Trả lời câu hỏi Vận dụng 2 trang 51 SGK Toán 12 Cùng khám phá
Sử dụng phương pháp tọa độ để giải bài toán sau:
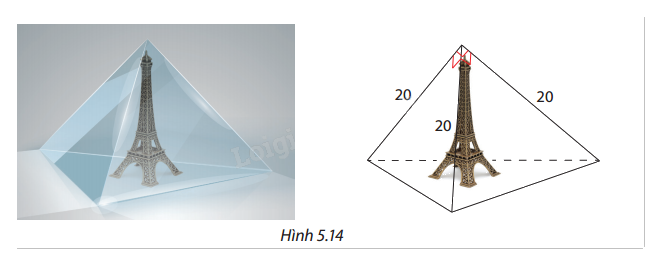
Bạn An muốn trưng bày một mô hình tháp Eiffel trong một cái hộp có dạng hình chóp tam giác đều với cạnh bên bằng 20 cm. Các mặt bên là các tam giác vuông và chân tháp nằm trên mặt đáy của cái hộp (Hình 5.14). Hỏi nếu mô hình tháp Eiffel này cao 11 cm thì có đặt được trong hộp không? Vì sao?
Phương pháp giải:
- Thiết lập hệ tọa độ Oxyz.
- Xác định tọa độ các đỉnh của tam giác đáy.
- Sử dụng định lý Pythagoras để tính chiều cao của hình chóp.
- So sánh chiều cao của mô hình với chiều cao của hình chóp.
- Kết luận mô hình có đặt vừa trong hộp hay không.
Lời giải chi tiết:
Gọi mặt đáy là tam giác ABC. Ta có các cạnh của tam giác ABC sẽ bằng:
\(AB = AC = BC = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,\,(cm)\)
Suy ra đường trung tuyến trong tam giác ABC là:
\(20\sqrt 2 .\frac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,\,(cm)\)
Đặt gốc toạ độ \(O(0;0;0)\) tại trung điểm của của BC, trục Oy trùng với BC, trục Oy nằm trên đường trung tuyến của điểm A. Từ đó suy ra các toạ độ của tam giác như sau:
\(A(10\sqrt 6 ;0;0),\,\,\,\,\,B(0; - 10;0),\,\,\,\,\,\,C(0;10;0)\)
Gọi toạ độ trọng tâm tam giác ABC là G, toạ độ của G là:
\(G\left( {\frac{{10\sqrt 6 }}{3};0;0} \right)\)
Gọi h là chiều cao của hình chóp, ta gọi đỉnh hình chóp là S. Vì hình chóp S.ABC là hình chóp tam giác đều nên toạ độ của S sẽ là: \(\left( {\frac{{10\sqrt 6 }}{3};0;h} \right)\).
Theo đề bài ta có độ dài các cạnh bên là 20cm, tương đương:
\(SA = 20 \Rightarrow \sqrt {{{\left( {10\sqrt 6 - \frac{{10\sqrt 6 }}{3}} \right)}^2} + {h^2}} = 20 = > {h^2} = {20^2} - {\left( {10\sqrt 6 - \frac{{10\sqrt 6 }}{3}} \right)^2}\)
\(h = \sqrt {\frac{{400}}{3}} = \frac{{20}}{{\sqrt 3 }} \approx 11,547\,\,\,(cm)\)
Vì chiều cao của hộp lớn hơn chiều cao của mô hình nên bạn An có thể đặt mô hình tháp Eiffel vào trong hộp.
Mục 4 của SGK Toán 12 tập 2 thường xoay quanh các chủ đề về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số, và các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Việc nắm vững các khái niệm và định lý liên quan là vô cùng quan trọng để giải quyết các bài tập trong mục này.
Các bài tập trong mục 4 trang 50, 51 thường được chia thành các dạng sau:
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 4 trang 50, 51, chúng tôi sẽ trình bày chi tiết lời giải của từng bài tập:
Lời giải:
y' = 3x2 - 4x + 5
Lời giải:
y' = 2x - 4
y' = 0 ⇔ x = 2
Khoảng đồng biến: (2, +∞)
Khoảng nghịch biến: (-∞, 2)
Lời giải:
y' = -2x + 6
y' = 0 ⇔ x = 3
Tính giá trị của hàm số tại các điểm x = 0, x = 3, x = 5:
y(0) = -5
y(3) = 4
y(5) = -10
Vậy, giá trị lớn nhất của hàm số trên đoạn [0, 5] là 4, đạt được tại x = 3. Giá trị nhỏ nhất của hàm số trên đoạn [0, 5] là -10, đạt được tại x = 5.
Để giải nhanh và hiệu quả các bài tập về đạo hàm và ứng dụng của đạo hàm, các em nên:
Ngoài SGK Toán 12 tập 2, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với bài giải chi tiết và những hướng dẫn hữu ích trên đây, các em sẽ tự tin hơn trong việc giải các bài tập mục 4 trang 50, 51 SGK Toán 12 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!