Chào mừng các em học sinh đến với bài giải bài tập 1.25 trang 35 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
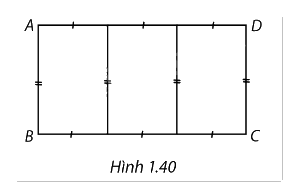
Người ta cần rào một mảnh đất hình chữ nhật ABCD có diện tích là 600 m². Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình 1.40). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60.000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài và chiều rộng của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm).
Đề bài
Người ta cần rào một mảnh đất hình chữ nhật ABCD có diện tích là 600 m². Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình 1.40). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60.000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài và chiều rộng của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
- Đặt chiều dài là 𝑥 và chiều rộng là 𝑦 của hình chữ nhật ABCD.
- Tính chi phí xây dựng hàng rào dựa trên chiều dài và chiều rộng.
- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.
- Sử dụng đạo hàm để tìm giá trị tối ưu.
Lời giải chi tiết
Gọi chiều dài là \(x\) \((0 < x \le 60)\) và chiều rộng là \(y\) \((0 < y \le x)\) của hình chữ nhật ABCD.
Diện tích của hình chữ nhật ABCD là: \(xy = 600\)
- Chi phí hàng rào ngoài là 2x+2y.
- Chi phí hàng rào bên trong là 2y.
-Tổng chi phí là: \(C = 60.000 \times (2x + 4y)\)
Viết hàm mục tiêu:
\(C = 60.000 \times \left( {2x + 4 \cdot \frac{{600}}{x}} \right) = 120.000 \times \left( {x + \frac{{1200}}{x}} \right)\)
Tìm giá trị cực trị: \(f(x) = x + \frac{{1200}}{x}\)
- Tính đạo hàm: \(f'(x) = 1 - \frac{{1200}}{{{x^2}}}\)
- Cho đạo hàm bằng 0: \(1 - \frac{{1200}}{{{x^2}}} = 0 \Rightarrow {x^2} = 1200 \Rightarrow x = \sqrt {1200} \approx 34,64(\;{\rm{m}})\)
Bảng biến thiên:
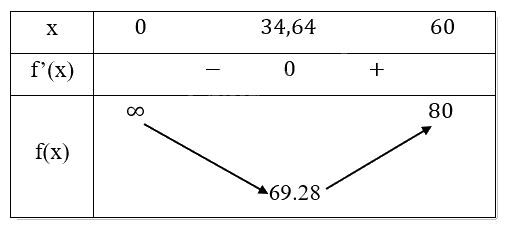
Nhận thấy tại vị trí x=34,64 thì giá trị của f(x) là nhỏ nhất
Tính \(y\): \(y = \frac{{600}}{x} \approx \frac{{600}}{{34,64}} \approx 17,32(\;{\rm{m}})\)
Tính chi phí:
\(L = 2x + 4y = 2.34,64 + 4.17,32 \approx 138,56m\)
\(C = 60000 \times 135,56 \approx 8313600\)
Kết luận: Để chi phí xây dựng hàng rào là thấp nhất thì
- Chiều dài của hình chữ nhật ABCD: \(x \approx 34,64\)m
- Chiều rộng của hình chữ nhật ABCD: \(y \approx 17,32\)m
- Tổng chi phí xây dựng hàng rào: 8313600 đồng.
Bài tập 1.25 trang 35 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số. Cụ thể, bài tập thường xoay quanh việc tìm đạo hàm, xét dấu đạo hàm, xác định các điểm cực trị và vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm, đồng thời rèn luyện kỹ năng giải toán một cách thành thạo.
Đề bài cụ thể của bài tập 1.25 sẽ khác nhau tùy theo từng phiên bản SGK. Tuy nhiên, cấu trúc chung của bài tập thường bao gồm:
Để giải bài tập 1.25 trang 35 SGK Toán 12 tập 1, học sinh có thể áp dụng các bước sau:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và vẽ đồ thị.
Giải:
| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| y' | + | - | + |
| Hàm số | Đồng biến | Nghịch biến | Đồng biến |
Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Điểm cực đại là (0; 2), điểm cực tiểu là (2; -2).
Vẽ đồ thị: Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm và khảo sát hàm số, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập khó.
Bài tập 1.25 trang 35 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ giải bài tập này một cách hiệu quả và đạt kết quả tốt.