Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 52, 53, 54 sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng: - Độ dài của vectơ. - Giá của vectơ. - Hai vectơ cùng phương, hai vectơ cùng hướng. - Hai vectơ bằng nhau. - Hai vectơ đối nhau. - Vectơ-không.
Trả lời câu hỏi Hoạt động 2 trang 52 SGK Toán 12 Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng:
- Độ dài của vectơ.
- Giá của vectơ.
- Hai vectơ cùng phương, hai vectơ cùng hướng.
- Hai vectơ bằng nhau.
- Hai vectơ đối nhau.
- Vectơ-không.
Phương pháp giải:
Các khái niệm liên quan đến vectơ trong không gian có trong Sách giáo khoa trang 52.
Lời giải chi tiết:
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vectơ \(\vec a\) được kí hiệu là \(|\vec a|\).
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
- Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).
- Vectơ-không có độ dài bằng 0 và cùng phương, cùng hướng với mọi vectơ.
Trả lời câu hỏi Hoạt động 2 trang 52 SGK Toán 12 Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng:
- Độ dài của vectơ.
- Giá của vectơ.
- Hai vectơ cùng phương, hai vectơ cùng hướng.
- Hai vectơ bằng nhau.
- Hai vectơ đối nhau.
- Vectơ-không.
Phương pháp giải:
Các khái niệm liên quan đến vectơ trong không gian có trong Sách giáo khoa trang 52.
Lời giải chi tiết:
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vectơ \(\vec a\) được kí hiệu là \(|\vec a|\).
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
- Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).
- Vectơ-không có độ dài bằng 0 và cùng phương, cùng hướng với mọi vectơ.
Trả lời câu hỏi Luyện tập 2 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Trong các vectơ khác \(\vec 0\), có điểm đầu và̀ điểm cuối là các đỉnh của hình hộp, hãy chỉ ra những vectơ:
- Cùng phương với vectơ \(\overrightarrow {AB} \);
- Bä̀ng vectơ \(\overrightarrow {AB} \);
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \).
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \) trong trường hợp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, có \(A{A^\prime } = \) a, \(AB = b,BC = c\) và \(\widehat {ABC} = {120^o}\).
Phương pháp giải:
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết:
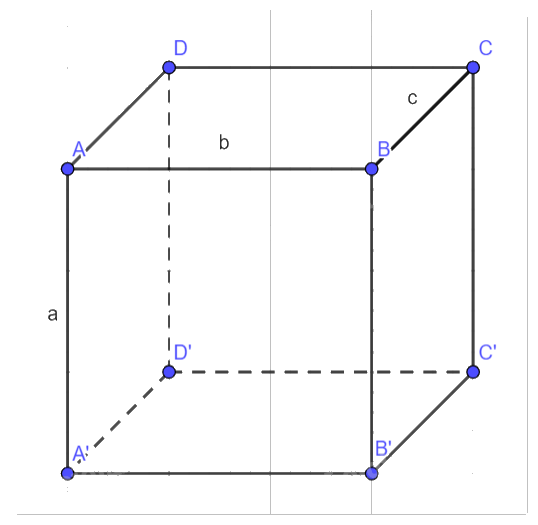
a) Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp:
- Cùng phương với vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {{A^\prime }{B^\prime }} \), \(\overrightarrow {DC} \), \(\overrightarrow {{D^\prime }{C^\prime }} \),\(\overrightarrow {{B^\prime }{A^\prime }} \), \(\overrightarrow {CD} \), \(\overrightarrow {{C^\prime }{D^\prime }} \),\(\overrightarrow {BA} \)
- Bằng vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {DC} = \overrightarrow {{D^\prime }{C^\prime }} \)
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \): \(\overrightarrow {{B^\prime }B} \),\(\overrightarrow {{C^\prime }C} \),\(\overrightarrow {{D^\prime }D} \),\(\overrightarrow {{A^\prime }A} \)
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \):
- Vì \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, suy ra tam giác \(AA'C'\) vuông tại \(A'\). Từ đó ta có:
\(\begin{array}{l}AC' = \sqrt {{{(AA')}^2} + {{(A'C')}^2}} = \sqrt {{a^2} + A{C^2}} = \sqrt {{a^2} + (A{B^2} + B{C^2} - 2.AB.BC.\cos (120^\circ )} \\AC' = \sqrt {{a^2} + {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right)} = \sqrt {{a^2} + {b^2} + {c^2} - bc} \end{array}\)
Vậy độ dài của vectơ \(\overrightarrow {A{C^\prime }} \)là: \(\sqrt {{a^2} + {b^2} + {c^2} - bc} \)
Trả lời câu hỏi Luyện tập 2 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Trong các vectơ khác \(\vec 0\), có điểm đầu và̀ điểm cuối là các đỉnh của hình hộp, hãy chỉ ra những vectơ:
- Cùng phương với vectơ \(\overrightarrow {AB} \);
- Bä̀ng vectơ \(\overrightarrow {AB} \);
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \).
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \) trong trường hợp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, có \(A{A^\prime } = \) a, \(AB = b,BC = c\) và \(\widehat {ABC} = {120^o}\).
Phương pháp giải:
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết:
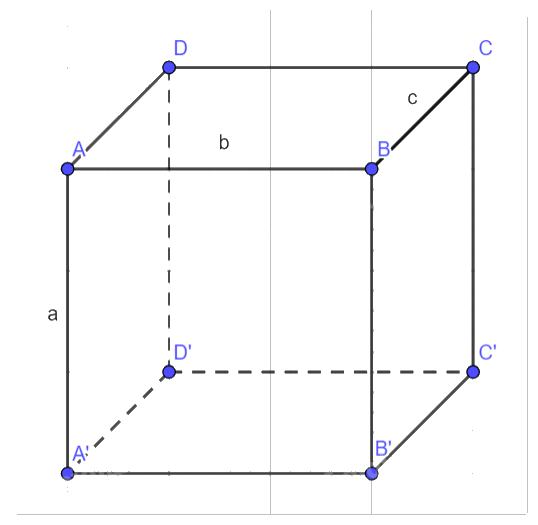
a) Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp:
- Cùng phương với vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {{A^\prime }{B^\prime }} \), \(\overrightarrow {DC} \), \(\overrightarrow {{D^\prime }{C^\prime }} \),\(\overrightarrow {{B^\prime }{A^\prime }} \), \(\overrightarrow {CD} \), \(\overrightarrow {{C^\prime }{D^\prime }} \),\(\overrightarrow {BA} \)
- Bằng vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {DC} = \overrightarrow {{D^\prime }{C^\prime }} \)
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \): \(\overrightarrow {{B^\prime }B} \),\(\overrightarrow {{C^\prime }C} \),\(\overrightarrow {{D^\prime }D} \),\(\overrightarrow {{A^\prime }A} \)
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \):
- Vì \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, suy ra tam giác \(AA'C'\) vuông tại \(A'\). Từ đó ta có:
\(\begin{array}{l}AC' = \sqrt {{{(AA')}^2} + {{(A'C')}^2}} = \sqrt {{a^2} + A{C^2}} = \sqrt {{a^2} + (A{B^2} + B{C^2} - 2.AB.BC.\cos (120^\circ )} \\AC' = \sqrt {{a^2} + {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right)} = \sqrt {{a^2} + {b^2} + {c^2} - bc} \end{array}\)
Vậy độ dài của vectơ \(\overrightarrow {A{C^\prime }} \)là: \(\sqrt {{a^2} + {b^2} + {c^2} - bc} \)
Mục 2 của SGK Toán 12 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của từng bài toán cũng rất quan trọng để lựa chọn phương pháp giải phù hợp.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến giới hạn). Để giải bài tập này, ta cần:
Ví dụ: (giải chi tiết bài tập 1 với các bước cụ thể)
Bài tập này có thể liên quan đến... (giả sử bài tập liên quan đến đạo hàm). Để giải quyết bài tập này, ta cần:
Ví dụ: (giải chi tiết bài tập 2 với các bước cụ thể)
Bài tập này thường là một bài toán tổng hợp, yêu cầu học sinh vận dụng kiến thức từ nhiều phần khác nhau của chương. Để giải bài tập này, ta cần:
Ví dụ: (giải chi tiết bài tập 3 với các bước cụ thể)
Để học toán hiệu quả, các em nên:
Khi giải bài tập Toán 12, các em cần chú ý:
Hy vọng rằng với những hướng dẫn chi tiết trên, các em sẽ tự tin giải quyết các bài tập trong mục 2 trang 52, 53, 54 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Chủ đề | Độ khó |
|---|---|---|
| Bài tập 1 | Giới hạn | Dễ |
| Bài tập 2 | Đạo hàm | Trung bình |
| Bài tập 3 | Tổng hợp | Khó |