Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 2, 3 và 4 của sách giáo khoa Toán 12 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
Tính đơn điệu của hàm số và dấu của đạo hàm
Trả lời câu hỏi Hoạt động 2 trang 4 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f(x) = {x^3} + 1\)
a) Bằng định nghĩa, hãy cho biết hàm \(f(x)\)có đồng biến trên \(R\) hay không
b) Hãy nhận xét về dấu của đạo hàm \(f'(x)\) trên \(R\)
Phương pháp giải:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\) và\({x_1} > {x_2}\)
Xét dấu của \(f({x_1}) - f({x_2})\)
b) Tính \(f'(x)\) qua đó xét dấu của \(f'(x)\)
Lời giải chi tiết:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\)và \({x_1} > {x_2}\)
Ta có: \(f({x_1}) - f({x_2})\)= \(({x_1} + 1) - ({x_2} + 1)\)= \({x_1} - {x_2}\)
Mà \({x_1} > {x_2}\) \( \Rightarrow {x_1} - {x_2} > 0\)
Nên \(f({x_1}) - f({x_2}) > 0\) \( \Rightarrow f({x_1}) > f({x_2})\)
Suy ra hàm số \(y = f(x) = {x^3} + 1\) đồng biến trên \(R\)
b) Ta có: \(f'(x) = 3{x^2}\)
Vì \(3{x^2} > 0\) với \(\forall x \in R\)
Nên \(f'(x) > 0\) với \(\forall x \in R\)
Trả lời câu hỏi Hoạt động 1 trang 2 SGK Toán 12 Cùng khám phá
Hình 1.2 là đồ thị (C) của hàm số \(y = f(x) = \frac{{ - 1}}{2}{x^2} + 3\)
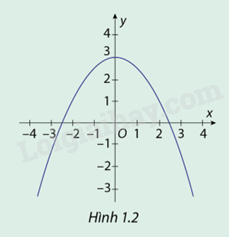
a) Quan sát đồ thị hàm số (C) và chỉ ra các khoảng đồng biến, nghịch biến của hàm số đã cho.
b) Xác định dấu của đạo hàm \(f'(x)\) khi \(x\)thuộc các khoảng đồng biến, nghịch biến ở câu.
c) Ghi lại và hoàn thành bảng biến thiên sau
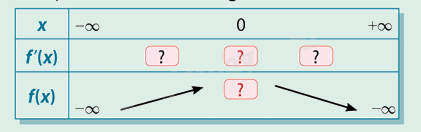
Phương pháp giải:
a) Sử dụng khái niệm hàm số đồng biến, hàm số nghịch biến trên khoảng (a;b)
Hàm số \(y = f(x)\)gọi là đồng biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} < {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
Hàm số \(y = f(x)\) gọi là nghịch biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} > {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
b) Chọn vài giá trị của x nằm trong khoảng đồng biến , nghịch biến ở câu a rồi thay vào \(f'(x)\)xem \(f'(x)\) có giá trị âm hay dương.
c) Áp dụng kết quả câu a và câu b rồi điền vào
Lời giải chi tiết:
a) Hàm số \(y = f(x)\) xác định trên R
Nhìn hình 1.2 ta thấy:
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) đồng biến trên khoảng \(( - \infty ;0)\)
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) nghịch biến trên khoảng \((0; + \infty )\)
b) Ta có \(f'(x) = - x\)
Ta thấy: Với \(x > 0\)thì \(f'(x) < 0\)
Với \(x < 0\) thì \(f'(x) > 0\)
c)
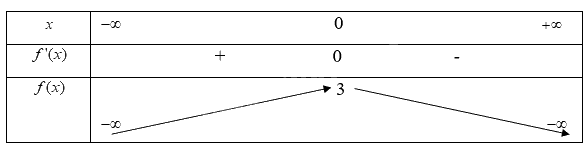
Trả lời câu hỏi Luyện tập 2 trang 5 SGK Toán 12 Kết nối tri thức
Xét tính đơn điệu của hàm số \(y = \sin x - x\)trên khoảng \(( - \pi ;\pi )\)
Phương pháp giải:
Bước 1: tính đạo hàm \(y'\)
Bước 2: xét dấu \(y'\) rồi lập bảng biến thiên
Bước 3: Từ bảng biến thiên nhận xét tính đơn điệu của hàm số
Lời giải chi tiết:
Hàm số đã cho xác định trên
Ta có: \(y' = \cos x - 1\)
Vì \(\cos x \le 1\)với \(\forall x \in R\)
Nên \(y' \le 0\)với \(\forall x \in R\)và \(y' = 0\)tại \(x = 0\)
Khi đó ta có bảng biến thiên:
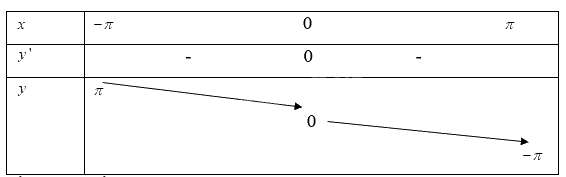
Vậy hàm số nghịch biến trên khoảng \(( - \pi ;\pi )\)
Trả lời câu hỏi Luyện tập 1 trang 4 SGK Toán 12 Kết nối tri thức
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Phương pháp giải:
Bước 1: Xét \(f'(x) = 0\)qua đó tìm x
Bước 2: Xét dấu \(f'(x)\)
Bước 3: lập bảng biến thiên
Lời giải chi tiết:
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
Hàm số trên xác định trên R\ {-3}
Ta có: \(f'(x) = \frac{{2(x + 3) - (2x - 1)}}{{{{(x + 3)}^2}}}\)
\(f'(x) = \frac{7}{{{{(x + 3)}^2}}}\)
Vì \(f'(x) > 0\)với \(\forall x \ne - 3\) từ đó ta có bảng biến thiên
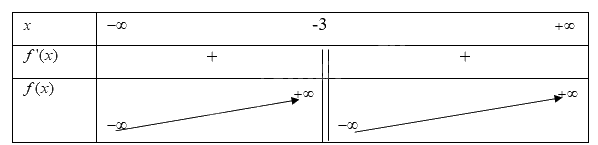
Từ bảng biến thiên ta có,
Hàm số \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\) đồng biến trên khoảng \(( - \infty ; - 3)\)và \(( - 3; + \infty )\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Hàm số trên xác định trên R
Ta có \(y = f'(x) = - \sin x\)
Xét \(f'(x) = - \sin x = 0\) \( \Rightarrow x = k\pi \)
Mà \(x \in (0;2\pi )\) \( \Rightarrow x = \pi \)
Khi đó ta có bảng biến thiên
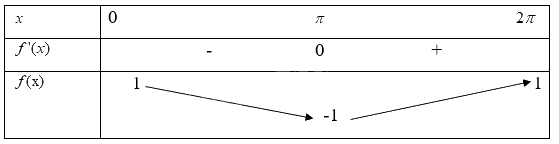
Từ bảng biến thiên ta có
Hàm số \(f(x) = \cos x\) đồng biến trên khoảng\((\pi ;2\pi )\)
Hàm số \(f(x) = \cos x\) nghịch biến trên khoảng\((0;\pi )\)
Trả lời câu hỏi Hoạt động 1 trang 2 SGK Toán 12 Cùng khám phá
Hình 1.2 là đồ thị (C) của hàm số \(y = f(x) = \frac{{ - 1}}{2}{x^2} + 3\)
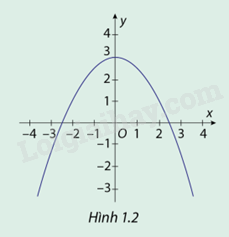
a) Quan sát đồ thị hàm số (C) và chỉ ra các khoảng đồng biến, nghịch biến của hàm số đã cho.
b) Xác định dấu của đạo hàm \(f'(x)\) khi \(x\)thuộc các khoảng đồng biến, nghịch biến ở câu.
c) Ghi lại và hoàn thành bảng biến thiên sau
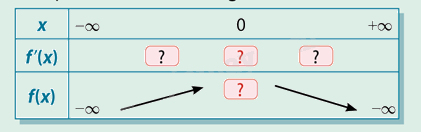
Phương pháp giải:
a) Sử dụng khái niệm hàm số đồng biến, hàm số nghịch biến trên khoảng (a;b)
Hàm số \(y = f(x)\)gọi là đồng biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} < {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
Hàm số \(y = f(x)\) gọi là nghịch biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} > {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
b) Chọn vài giá trị của x nằm trong khoảng đồng biến , nghịch biến ở câu a rồi thay vào \(f'(x)\)xem \(f'(x)\) có giá trị âm hay dương.
c) Áp dụng kết quả câu a và câu b rồi điền vào
Lời giải chi tiết:
a) Hàm số \(y = f(x)\) xác định trên R
Nhìn hình 1.2 ta thấy:
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) đồng biến trên khoảng \(( - \infty ;0)\)
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) nghịch biến trên khoảng \((0; + \infty )\)
b) Ta có \(f'(x) = - x\)
Ta thấy: Với \(x > 0\)thì \(f'(x) < 0\)
Với \(x < 0\) thì \(f'(x) > 0\)
c)
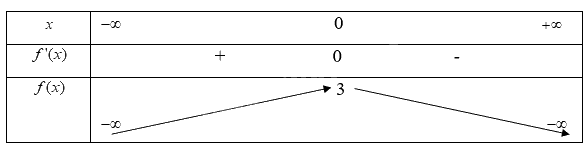
Trả lời câu hỏi Luyện tập 1 trang 4 SGK Toán 12 Kết nối tri thức
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Phương pháp giải:
Bước 1: Xét \(f'(x) = 0\)qua đó tìm x
Bước 2: Xét dấu \(f'(x)\)
Bước 3: lập bảng biến thiên
Lời giải chi tiết:
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
Hàm số trên xác định trên R\ {-3}
Ta có: \(f'(x) = \frac{{2(x + 3) - (2x - 1)}}{{{{(x + 3)}^2}}}\)
\(f'(x) = \frac{7}{{{{(x + 3)}^2}}}\)
Vì \(f'(x) > 0\)với \(\forall x \ne - 3\) từ đó ta có bảng biến thiên
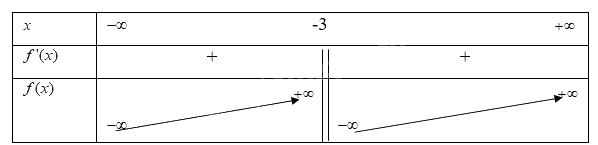
Từ bảng biến thiên ta có,
Hàm số \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\) đồng biến trên khoảng \(( - \infty ; - 3)\)và \(( - 3; + \infty )\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Hàm số trên xác định trên R
Ta có \(y = f'(x) = - \sin x\)
Xét \(f'(x) = - \sin x = 0\) \( \Rightarrow x = k\pi \)
Mà \(x \in (0;2\pi )\) \( \Rightarrow x = \pi \)
Khi đó ta có bảng biến thiên
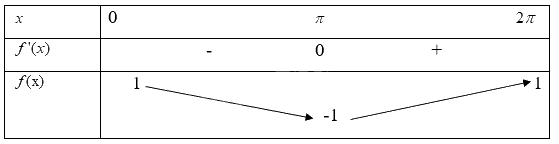
Từ bảng biến thiên ta có
Hàm số \(f(x) = \cos x\) đồng biến trên khoảng\((\pi ;2\pi )\)
Hàm số \(f(x) = \cos x\) nghịch biến trên khoảng\((0;\pi )\)
Trả lời câu hỏi Hoạt động 2 trang 4 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f(x) = {x^3} + 1\)
a) Bằng định nghĩa, hãy cho biết hàm \(f(x)\)có đồng biến trên \(R\) hay không
b) Hãy nhận xét về dấu của đạo hàm \(f'(x)\) trên \(R\)
Phương pháp giải:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\) và\({x_1} > {x_2}\)
Xét dấu của \(f({x_1}) - f({x_2})\)
b) Tính \(f'(x)\) qua đó xét dấu của \(f'(x)\)
Lời giải chi tiết:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\)và \({x_1} > {x_2}\)
Ta có: \(f({x_1}) - f({x_2})\)= \(({x_1} + 1) - ({x_2} + 1)\)= \({x_1} - {x_2}\)
Mà \({x_1} > {x_2}\) \( \Rightarrow {x_1} - {x_2} > 0\)
Nên \(f({x_1}) - f({x_2}) > 0\) \( \Rightarrow f({x_1}) > f({x_2})\)
Suy ra hàm số \(y = f(x) = {x^3} + 1\) đồng biến trên \(R\)
b) Ta có: \(f'(x) = 3{x^2}\)
Vì \(3{x^2} > 0\) với \(\forall x \in R\)
Nên \(f'(x) > 0\) với \(\forall x \in R\)
Trả lời câu hỏi Luyện tập 2 trang 5 SGK Toán 12 Kết nối tri thức
Xét tính đơn điệu của hàm số \(y = \sin x - x\)trên khoảng \(( - \pi ;\pi )\)
Phương pháp giải:
Bước 1: tính đạo hàm \(y'\)
Bước 2: xét dấu \(y'\) rồi lập bảng biến thiên
Bước 3: Từ bảng biến thiên nhận xét tính đơn điệu của hàm số
Lời giải chi tiết:
Hàm số đã cho xác định trên
Ta có: \(y' = \cos x - 1\)
Vì \(\cos x \le 1\)với \(\forall x \in R\)
Nên \(y' \le 0\)với \(\forall x \in R\)và \(y' = 0\)tại \(x = 0\)
Khi đó ta có bảng biến thiên:
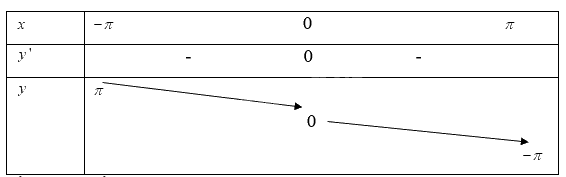
Vậy hàm số nghịch biến trên khoảng \(( - \pi ;\pi )\)
Mục 1 của SGK Toán 12 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị hàm số từ chương trình Toán 11, đồng thời giới thiệu một số khái niệm mới liên quan đến giới hạn và liên tục. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục 1, trang 2, 3 và 4 của SGK Toán 12 tập 1. Mỗi bài giải sẽ được trình bày một cách rõ ràng, dễ hiểu, bao gồm:
(Nội dung bài tập 1 và lời giải chi tiết)
Ví dụ, bài tập 1 có thể yêu cầu xét tính đơn điệu của hàm số. Lời giải sẽ bao gồm việc tính đạo hàm, xét dấu đạo hàm và kết luận về tính đơn điệu của hàm số.
(Nội dung bài tập 2 và lời giải chi tiết)
Bài tập 2 có thể liên quan đến việc tìm tập xác định của hàm số. Lời giải sẽ bao gồm việc xác định các điều kiện để hàm số có nghĩa và tìm tập xác định tương ứng.
(Nội dung bài tập 3 và lời giải chi tiết)
Bài tập 3 có thể yêu cầu vẽ đồ thị hàm số. Lời giải sẽ bao gồm việc xác định các điểm đặc biệt của đồ thị (điểm cực trị, điểm uốn, giao điểm với các trục tọa độ) và vẽ đồ thị dựa trên các thông tin đó.
(Nội dung bài tập 4 và lời giải chi tiết)
Bài tập 4 có thể liên quan đến giới hạn của hàm số. Lời giải sẽ bao gồm việc áp dụng các quy tắc tính giới hạn và tìm giới hạn của hàm số.
Trong mục 1, các em có thể gặp các dạng bài tập sau:
Để học tốt Toán 12 tập 1, các em nên:
Hy vọng rằng với những giải thích chi tiết và hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 2,3,4 SGK Toán 12 tập 1. Chúc các em học tập tốt và đạt kết quả cao!