Chào mừng các em học sinh đến với bài giải bài tập 2.9 trang 65 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Cho tứ diện ABCD. Hai điểm M và N theo thứ tự là trung điểm của BC và AD. Cho biết AB = 10, CD = 6, MN = 7. a) Chứng minh rằng (overrightarrow {NM} = frac{1}{2}left( {overrightarrow {AB} + overrightarrow {DC} } right)). b) Từ kết quả câu a, hãy tính (overrightarrow {AB} .overrightarrow {DC} ). c) Tính (left( {overrightarrow {AB} ,overrightarrow {DC} } right)).
Đề bài
Cho tứ diện ABCD. Hai điểm M và N theo thứ tự là trung điểm của BC và AD. Cho biết AB = 10, CD = 6, MN = 7.
a) Chứng minh rằng \(\overrightarrow {NM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).
b) Từ kết quả câu a, hãy tính \(\overrightarrow {AB} .\overrightarrow {DC} \).
c) Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right)\).
Phương pháp giải - Xem chi tiết
a) Để chứng minh \(\overrightarrow {NM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\), ta cần sử dụng tính chất trung điểm và phép cộng vectơ.
b) Sử dụng kết quả từ phần a) để tính tích vô hướng \(\overrightarrow {AB} \cdot \overrightarrow {DC} \). Áp dụng tính chất “Bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó”.
c) Sử dụng tích vô hướng để tìm góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \).
\(\cos \theta = \frac{{\overrightarrow {AB} \cdot \overrightarrow {DC} }}{{|\overrightarrow {AB} | \cdot |\overrightarrow {DC} |}}\)
Lời giải chi tiết
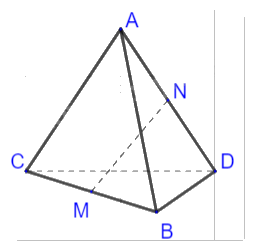
a) Chứng minh \(\overrightarrow {NM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\):
- Vì \(M\) là trung điểm của BC, nên \(\overrightarrow {BM} = \frac{1}{2}\overrightarrow {BC} \).
- Vì \(N\) là trung điểm của AD, nên \(\overrightarrow {AN} = \frac{1}{2}\overrightarrow {AD} \).
- Vectơ \(\overrightarrow {NM} \) có thể được viết là: \(\overrightarrow {NM} = \overrightarrow {NB} + \overrightarrow {BM} \).
Với: \(\overrightarrow {NB} = \overrightarrow {NA} + \overrightarrow {AB} = \frac{1}{2}\overrightarrow {DA} + \overrightarrow {AB} \)
Và: \(\overrightarrow {BM} = \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {BD} + \overrightarrow {DC} } \right)\).
Suy ra: \(\overrightarrow {NM} = \frac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {BD} } \right) + \overrightarrow {AB} + \frac{1}{2}\overrightarrow {DC} = \frac{1}{2}\overrightarrow {BA} + \overrightarrow {AB} + \frac{1}{2}\overrightarrow {DC} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\).
b) Từ kết quả câu a, tính \(\overrightarrow {AB} \cdot \overrightarrow {DC} \):
- Từ câu a, ta có:
\(\overrightarrow {NM} \cdot \overrightarrow {NM} = \frac{1}{4}(\overrightarrow {AB} + \overrightarrow {DC} ) \cdot (\overrightarrow {AB} + \overrightarrow {DC} )\).
Biểu thức này mở rộng thành:
\(\frac{1}{4}(\overrightarrow {AB} \cdot \overrightarrow {AB} + 2\overrightarrow {AB} \cdot \overrightarrow {DC} + \overrightarrow {DC} \cdot \overrightarrow {DC} )\).
Biết rằng \(\overrightarrow {NM} \cdot \overrightarrow {NM} = M{N^2} = 49\), \(AB = 10\), \(DC = 6\), ta suy ra:
\(49 = \frac{1}{4}(100 + 2\overrightarrow {AB} \cdot \overrightarrow {DC} + 36)\).
\(49 = \frac{1}{4}(136 + 2\overrightarrow {AB} \cdot \overrightarrow {DC} )\).
\(196 = 136 + 2\overrightarrow {AB} \cdot \overrightarrow {DC} \).
\(\overrightarrow {AB} \cdot \overrightarrow {DC} = 30\).
c) Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right)\):
- Góc giữa hai vectơ được tính bởi:
\(\cos \theta = \frac{{\overrightarrow {AB} \cdot \overrightarrow {DC} }}{{|\overrightarrow {AB} | \cdot |\overrightarrow {DC} |}}\).
\(\cos \theta = \frac{{30}}{{10 \cdot 6}} = \frac{1}{2}\).
Suy ra \(\theta = {60^\circ }\).
Bài tập 2.9 trang 65 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số. Cụ thể, bài tập thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị của hàm số, và vẽ đồ thị hàm số.
Các dạng bài tập 2.9 thường bao gồm:
Để giải bài tập 2.9 một cách hiệu quả, học sinh cần nắm vững các bước sau:
Giả sử bài tập yêu cầu khảo sát hàm số y = x3 - 3x2 + 2.
Giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | ĐB | NB |
Giaitoan.edu.vn cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để học Toán 12 hiệu quả và đạt kết quả cao!