Chào mừng các em học sinh đến với bài giải bài tập 3.7 trang 102 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Ngoài ra, chúng tôi còn có các bài giảng video, bài tập trắc nghiệm và các tài liệu học tập khác để hỗ trợ các em trong quá trình học tập.
Nhà máy đường kiểm tra khối lượng các gói đường do một máy đóng gói tự động thực hiện. Kết quả kiểm tra được biểu diễn trong bảng dưới đây:
Đề bài
Nhà máy đường kiểm tra khối lượng các gói đường do một máy đóng gói tự động thực hiện. Kết quả kiểm tra được biểu diễn trong bảng dưới đây:
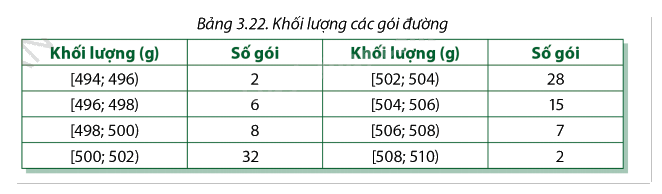
a) Tính trung bình và độ lệch chuẩn của khối lượng các gói đường.
b) Có thể nói là máy vận hành tốt hay không nếu như tiêu chuẩn mong muốn của nhà máy là khối lượng trung bình nằm trong khoảng 500 – 504 gam và độ lệch chuẩn nhỏ hơn 3 gam?
Phương pháp giải - Xem chi tiết
- Công thức tính trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)
Lời giải chi tiết
a) Tính trung điểm của từng lớp khối lượng.

Tính trung binh \(\overline x \).
\(\bar x = \frac{{2 \cdot 495 + 6 \cdot 497 + 8 \cdot 499 + 32 \cdot 501 + 28 \cdot 503 + 15 \cdot 505 + 7 \cdot 507 + 2 \cdot 509}}{{2 + 6 + 8 + 32 + 28 + 15 + 7 + 2}}\)
\(\bar x = \frac{{990 + 2982 + 3992 + 16032 + 14084 + 7575 + 3549 + 1018}}{{100}} = \frac{{50222}}{{100}} = 502,22\;{\rm{g}}\)
Tính \(\sum {{f_i}x_i^2} \)
\(\sum {{f_i}} x_i^2 = 2 \cdot {(495)^2} + 6 \cdot {(497)^2} + 8 \cdot {(499)^2} + 32 \cdot {(501)^2} + 28 \cdot {(503)^2} + 15 \cdot {(505)^2} + 7 \cdot {(507)^2} + 2 \cdot {(509)^2}\)
\(\sum {{f_i}} x_i^2 = 2 \cdot 245025 + 6 \cdot 247009 + 8 \cdot 249001 + 32 \cdot 251001 + 28 \cdot 253009 + 15 \cdot 255025 + 7 \cdot 257049 + 2 \cdot 259081\)
\(\sum {{f_i}} x_i^2 = 490050 + 1482054 + 1992008 + 8032032 + 7084252 + 3825375 + 1799343 + 518162 = 25223276\)
Độ lệch chuẩn của khối lượng các gói đường là:
\(S = \sqrt {\frac{{25223276}}{{100}} - {{\left( {502,22} \right)}^2}} \approx 2,798g\)
b) Khối lượng trung bình \(\overline x = 502,22\) nằm trong khoảng yêu cầu [500,504]. Độ lệch tiêu chuẩn \(S \approx 2,798\)g cũng bé hơn mức yêu cầu 3g nên có thể kết luận máy hoạt động đúng tiêu chuẩn mong muốn.
Bài tập 3.7 trang 102 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số, khảo sát sự biến thiên của hàm số và giải các bài toán thực tế liên quan đến tối ưu hóa.
Bài tập 3.7 thường có dạng như sau: Cho hàm số y = f(x). Hãy tìm các điểm cực trị của hàm số và khảo sát sự biến thiên của hàm số.
Xét hàm số y = x3 - 3x2 + 2. Ta thực hiện các bước sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Kiến thức về đạo hàm và ứng dụng của đạo hàm trong bài tập 3.7 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Bài tập 3.7 trang 102 SGK Toán 12 tập 1 là một bài toán quan trọng và có nhiều ứng dụng thực tế. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học sinh đạt kết quả tốt trong môn Toán và có thể áp dụng vào các lĩnh vực khác nhau trong cuộc sống.