Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 74, 75, 76 SGK Toán 12 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, chính xác, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, đạt kết quả tốt nhất trong môn Toán.
Trong không gian Oxyz, cho điểm (M(x;y;z)), mặt cầu S có tâm (I(a;b;c)) và bán kính (r).
Trả lời câu hỏi Luyện tập 3 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, viết phương trình mặt cầu \((S)\):
a) Có tâm \(I(2; - 1;0)\) và đi qua điểm \(M(4;1; - 2)\).
b) Có đường kính AB với \(A(0;1;3)\), \(B(4; - 5; - 1)\).
Phương pháp giải:
a)
- Tìm bán kính \(r\) của mặt cầu bằng cách tính khoảng cách IM.
- Sử dụng phương trình mặt cầu với tâm \(I(a;b;c)\) và bán kính \(r\):
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
b)
- Tìm tâm I của mặt cầu là trung điểm của đoạn AB.
- Tính bán kính \(r\) bằng nửa độ dài của AB.
- Dùng phương trình mặt cầu với tâm I và bán kính r.
Lời giải chi tiết:
a)
- Tâm \(I(2; - 1;0)\), điểm \(M(4;1; - 2)\).
- Tính bán kính:
\(r = IM = \sqrt {{{(4 - 2)}^2} + {{(1 + 1)}^2} + {{( - 2 - 0)}^2}} = \sqrt {{2^2} + {2^2} + {{( - 2)}^2}} = \sqrt {4 + 4 + 4} = \sqrt {12} = 2\sqrt 3 .\)
- Phương trình mặt cầu:
\({(x - 2)^2} + {(y + 1)^2} + {z^2} = {(2\sqrt 3 )^2} = 12.\)
Vậy phương trình mặt cầu \(S\) là:
\({(x - 2)^2} + {(y + 1)^2} + {z^2} = 12.\)
b)
- Trung điểm I của đoạn AB là:
\(I = \left( {\frac{{0 + 4}}{2};\frac{{1 - 5}}{2};\frac{{3 - 1}}{2}} \right) = (2; - 2;1).\)
- Tính bán kính \(r\) bằng nửa độ dài AB:
\(r = \frac{{AB}}{2} = \frac{{\sqrt {{{(4 - 0)}^2} + {{( - 5 - 1)}^2} + {{( - 1 - 3)}^2}} }}{2} = \frac{{\sqrt {{4^2} + {{( - 6)}^2} + {{( - 4)}^2}} }}{2} = \frac{{\sqrt {16 + 36 + 16} }}{2} = \frac{{\sqrt {68} }}{2} = \frac{{2\sqrt {17} }}{2} = \sqrt {17} .\)
- Phương trình mặt cầu:
\({(x - 2)^2} + {(y + 2)^2} + {(z - 1)^2} = {(\sqrt {17} )^2} = 17.\)
Vậy phương trình mặt cầu \(S\) là:
\({(x - 2)^2} + {(y + 2)^2} + {(z - 1)^2} = 17.\)
Trả lời câu hỏi Luyện tập 2 trang 74 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xác định tâm I và bán kính r của mặt cầu có phương trình:
a) \({(x + 3)^2} + {(y - 2)^2} + {(z + 3)^2} = 9\)
b) \({x^2} + {(y + 2)^2} + {z^2} = 1\)
Phương pháp giải:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm \(I(a;b;c)\) và bán kính r là:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
Lời giải chi tiết:
a) Ta có: \({(x + 3)^2} + {(y - 2)^2} + {(z + 3)^2} = 9 \Leftrightarrow {(x + 3)^2} + {(y - 2)^2} + {(z + 3)^2} = {3^2}\)
Vậy đây là phương trình mặt cầu có tâm \(I( - 3;2; - 3)\) và bán kính \(r = 3\).
b) Ta có:
\({x^2} + {(y + 2)^2} + {z^2} = 1 \Leftrightarrow {(x - 0)^2} + {(y + 2)^2} + {(z - 0)^2} = {1^2}\)
Vậy đây là phương trình mặt cầu có tâm \(I(0; - 2;0)\) và bán kính \(r = 1\).
Trả lời câu hỏi Hoạt động 3 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xét mặt cầu S có phương trình:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}\) (1). Khai triển (1), giả sử ta được:
\((1) \Leftrightarrow {x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0.\)
a) Tính A, B, C, D của (2) theo a, b, c, r của (1).
b) Xác định dấu của \({A^2} + {B^2} + {C^2} - D\).
c) Tìm tâm I và bán kính \(r\) của mặt cầu (S) theo A, B, C, D.
Phương pháp giải:
a) Khai triển phương trình mặt cầu và so sánh hệ số với phương trình đã cho.
b) Tính biểu thức \({A^2} + {B^2} + {C^2} - D\) dựa trên các giá trị của A, B, C, và D.
c) Tìm tọa độ tâm và bán kính mặt cầu S bằng cách đưa phương trình về dạng chuẩn.
Lời giải chi tiết:
a)
Khai triển phương trình mặt cầu:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
Ta có:
\({x^2} - 2ax + {a^2} + {y^2} - 2by + {b^2} + {z^2} - 2cz + {c^2} = {r^2}.\)
Rút gọn, ta được:
\({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + ({a^2} + {b^2} + {c^2} - {r^2}) = 0.\)
So sánh với phương trình đã cho:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0,\)
Suy ra:
\(A = - a,\quad B = - b,\quad C = - c,\quad D = {a^2} + {b^2} + {c^2} - {r^2}.\)
b)
Tính \({A^2} + {B^2} + {C^2} - D\):
\({A^2} + {B^2} + {C^2} - D = {( - a)^2} + {( - b)^2} + {( - c)^2} - ({a^2} + {b^2} + {c^2} - {r^2}).\)
\({A^2} + {B^2} + {C^2} - D = {a^2} + {b^2} + {c^2} - ({a^2} + {b^2} + {c^2}) + {r^2} = {r^2} > 0\)
c)
Từ \(A = - a\), \(B = - b\), \(C = - c\), suy ra:
\(a = - A,\quad b = - B,\quad c = - C.\)
Tọa độ tâm \(I\) của mặt cầu là \(I( - A, - B, - C)\). Bán kính \(r\) của mặt cầu là:
\(r = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)
Vậy, tâm và bán kính của mặt cầu \(S\) là:
\(I( - A, - B, - C),\quad r = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)
Trả lời câu hỏi Luyện tập 4 trang 76 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xác định tâm I và bán kính \(r\) của mặt cầu có phương trình:
a) \({x^2} + {y^2} + {z^2} + 4x - 2y + 1 = 0\).
b) \(3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y - 9z + 1 = 0\).
Phương pháp giải:
a) Với phương trình mặt cầu dạng tổng quát \({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0\):
- Tìm tọa độ tâm \(I(a,b,c)\) với
\(a = - A\), \(b = - B\), \(c = - C\).
- Tính bán kính \(r = \sqrt {{a^2} + {b^2} + {c^2} - D} \).
b) Nếu phương trình có hệ số khác 1 cho các x^2, y^2, z^2 thì chia cả hai vế cho hệ số đó để đưa về dạng chuẩn.
Lời giải chi tiết:
a) Phương trình mặt cầu:
\({x^2} + {y^2} + {z^2} + 4x - 2y + 1 = 0.\)
So sánh với phương trình mặt cầu tổng quát:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0,\)
ta có:
\(2A = 4 \Rightarrow A = 2,\quad 2B = - 2 \Rightarrow B = - 1,\quad 2C = 0 \Rightarrow C = 0,\quad D = 1.\)
Vậy:
\(a = - A = - 2,\quad b = - B = 1,\quad c = - C = 0.\)
Tâm \(I( - 2,1,0)\). Bán kính:
\(r = \sqrt {{a^2} + {b^2} + {c^2} - D} = \sqrt {{{( - 2)}^2} + {1^2} + {0^2} - 1} = \sqrt {4 + 1 - 1} = \sqrt 4 = 2.\)
Vậy phương trình mặt cầu có tâm \(I( - 2,1,0)\) và bán kính \(r = 2\).
b)
Phương trình mặt cầu:
\(3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y - 9z + 1 = 0.\)
Chia cả hai vế cho \(3\):
\({x^2} + {y^2} + {z^2} + 2x + 4y - 3z + \frac{1}{3} = 0.\)
So sánh với phương trình mặt cầu tổng quát:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0,\)
ta có:
\(2A = 2 \Rightarrow A = 1,\quad 2B = 4 \Rightarrow B = 2,\quad 2C = - 3 \Rightarrow C = - \frac{3}{2},\quad D = \frac{1}{3}.\)
Vậy:
\(a = - A = - 1,\quad b = - B = - 2,\quad c = - C = \frac{3}{2}.\)
Tâm \(I( - 1, - 2,\frac{3}{2})\). Bán kính:
\(r = \sqrt {{a^2} + {b^2} + {c^2} - D} = \sqrt {{{( - 1)}^2} + {{( - 2)}^2} + {{\left( {\frac{3}{2}} \right)}^2} - \frac{1}{3}} = \sqrt {1 + 4 + \frac{9}{4} - \frac{1}{3}} .\)
Tính tiếp:
\(r = \sqrt {\frac{{12 + 48 + 27 - 4}}{{12}}} = \sqrt {\frac{{83}}{{12}}} = \frac{{\sqrt {83} }}{2}.\)
Vậy phương trình mặt cầu có tâm \(I( - 1, - 2,\frac{3}{2})\) và bán kính \(r = \frac{{\sqrt {83} }}{2}\).
Trả lời câu hỏi Hoạt động 2 trang 74 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho điểm \(M(x;y;z)\), mặt cầu S có tâm \(I(a;b;c)\) và bán kính \(r\).
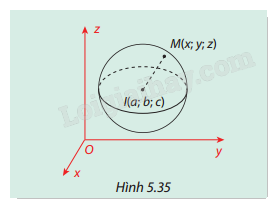
a) Tính độ dài đoạn thẳng IM theo a, b, c, x, y, z.
b) Thay ? bằng một biểu thức hoặc một giá trị thích hợp để có phương trình của mặt cầu.
\(M \in (S) \Leftrightarrow IM = ? \Leftrightarrow \sqrt ? = r \Leftrightarrow {(x - ?)^2} + {(y - ?)^2} + {(z - ?)^2} = {r^2}.\)
Phương pháp giải:
a) Sử dụng công thức khoảng cách giữa hai điểm trong không gian để tính độ dài IM theo tọa độ.
b) Sử dụng tính chất khoảng cách từ tâm tới một điểm bất kỳ thuộc mặt cầu đều bằng bán kính của mặt cầu đó.
Lời giải chi tiết:
a) Khoảng cách từ \(I(a;b;c)\) đến \(M(x;y;z)\) là:
\(IM = \sqrt {{{(x - a)}^2} + {{(y - b)}^2} + {{(z - c)}^2}} .\)
b) Biểu thức sau khi thay ? là:
\(M \in (S) \Leftrightarrow IM = r \Leftrightarrow \sqrt {{{(x - a)}^2} + {{(y - b)}^2} + {{(z - c)}^2}} = r \Leftrightarrow {(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
Trả lời câu hỏi Vận dụng 1 trang 76 SGK Toán 12 Cùng khám phá
Trong hệ trục Oxyz cho trước (đơn vị trên trục là mét), một trạm thu phát sóng 5G có bán kính vùng phủ sóng của trạm ở ngưỡng 600 m được đặt ở vị trí \(I(200;450;60)\)
a) Lập phương trình mặt cầu mô tả ranh giới bên ngoài và bên trong của vùng phủ sóng.
b) Nếu người dùng điện thoại đang ở vị trí \(A( - 100;50;10)\) thì có thể sử dụng dịch vụ của trạm này không? Vì sao?
Phương pháp giải:
a) Dùng phương trình mặt cầu với tâm I và bán kính \(r\) đã cho.
b) Tính khoảng cách IA và so sánh với bán kính \(r\).
Lời giải chi tiết:
a)
Phương trình mặt cầu với tâm \(I(200;450;60)\) và bán kính \(r = 600\):
\({(x - 200)^2} + {(y - 450)^2} + {(z - 60)^2} = {600^2} = 360000.\)
Vậy phương trình mặt cầu mô tả vùng phủ sóng là:
\({(x - 200)^2} + {(y - 450)^2} + {(z - 60)^2} = 360000.\)
b)
Tính khoảng cách IA:
\(IA = \sqrt {{{( - 100 - 200)}^2} + {{(50 - 450)}^2} + {{(10 - 60)}^2}} = \sqrt {{{( - 300)}^2} + {{( - 400)}^2} + {{( - 50)}^2}} .\)
\(IA = \sqrt {90000 + 160000 + 2500} = \sqrt {252500} \approx 502.5.\)
Vì \(IA \approx 502.5 < 600\), nên người dùng điện thoại ở vị trí \(A( - 100;50;10)\) nằm trong vùng phủ sóng của trạm và có thể sử dụng dịch vụ của trạm này.
Trả lời câu hỏi Vận dụng 2 trang 76 SGK Toán 12 Cùng khám phá
Giả sử người ta biểu diễn mô phỏng của tòa nhà Ericsson Globe ở phần Khởi động trong hệ trục tọa độ Oxyz bởi một mặt cầu có tâm I, đường kính 110 m và \(OA = 85\) m như hình vẽ (đơn vị trên trục là mét). Hãy viết phương trình của mặt cầu này.
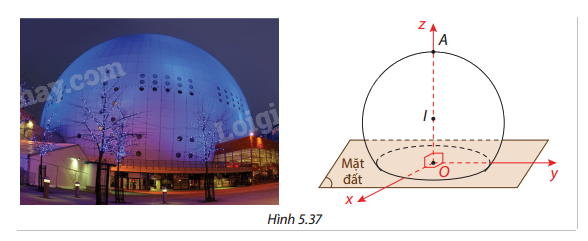
Phương pháp giải:
1. Xác định tọa độ của tâm mặt cầu I:
- Vì tâm mặt cầu nằm trên trục Oz, nên tọa độ của I sẽ có dạng \((0,0,{z_0})\).
- Sử dụng thông tin khoảng cách từ O đến I để tìm \({z_0}\).
2. Viết phương trình của mặt cầu:
- Phương trình tổng quát của mặt cầu có tâm \(I(a,b,c)\) và bán kính \(R\) là:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\)
- Thay tọa độ tâm và bán kính vào phương trình trên để hoàn thành lời giải.
Lời giải chi tiết:
1. Xác định tọa độ tâm \(I\):
Do \(OA = 85\) m và bán kính của mặt cầu \(R = \frac{{110}}{2} = 55\) m, nên khoảng cách từ \(O\) đến \(I\) là:
\(OI = OA - R = 85 - 55 = 30 {\rm{m}}\).
Vậy tọa độ của \(I\) là \((0,0,30)\).
2. Viết phương trình của mặt cầu:
Phương trình mặt cầu với tâm \(I(0,0,30)\) và bán kính \(R = 55\) là:
\({(x - 0)^2} + {(y - 0)^2} + {(z - 30)^2} = {55^2}\)
\( \Leftrightarrow{x^2} + {y^2} + {(z - 30)^2} = 3025\).
Trả lời câu hỏi Hoạt động 2 trang 74 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho điểm \(M(x;y;z)\), mặt cầu S có tâm \(I(a;b;c)\) và bán kính \(r\).
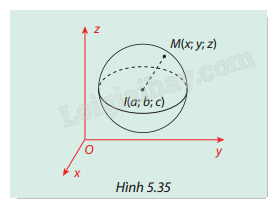
a) Tính độ dài đoạn thẳng IM theo a, b, c, x, y, z.
b) Thay ? bằng một biểu thức hoặc một giá trị thích hợp để có phương trình của mặt cầu.
\(M \in (S) \Leftrightarrow IM = ? \Leftrightarrow \sqrt ? = r \Leftrightarrow {(x - ?)^2} + {(y - ?)^2} + {(z - ?)^2} = {r^2}.\)
Phương pháp giải:
a) Sử dụng công thức khoảng cách giữa hai điểm trong không gian để tính độ dài IM theo tọa độ.
b) Sử dụng tính chất khoảng cách từ tâm tới một điểm bất kỳ thuộc mặt cầu đều bằng bán kính của mặt cầu đó.
Lời giải chi tiết:
a) Khoảng cách từ \(I(a;b;c)\) đến \(M(x;y;z)\) là:
\(IM = \sqrt {{{(x - a)}^2} + {{(y - b)}^2} + {{(z - c)}^2}} .\)
b) Biểu thức sau khi thay ? là:
\(M \in (S) \Leftrightarrow IM = r \Leftrightarrow \sqrt {{{(x - a)}^2} + {{(y - b)}^2} + {{(z - c)}^2}} = r \Leftrightarrow {(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
Trả lời câu hỏi Luyện tập 2 trang 74 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xác định tâm I và bán kính r của mặt cầu có phương trình:
a) \({(x + 3)^2} + {(y - 2)^2} + {(z + 3)^2} = 9\)
b) \({x^2} + {(y + 2)^2} + {z^2} = 1\)
Phương pháp giải:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm \(I(a;b;c)\) và bán kính r là:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
Lời giải chi tiết:
a) Ta có: \({(x + 3)^2} + {(y - 2)^2} + {(z + 3)^2} = 9 \Leftrightarrow {(x + 3)^2} + {(y - 2)^2} + {(z + 3)^2} = {3^2}\)
Vậy đây là phương trình mặt cầu có tâm \(I( - 3;2; - 3)\) và bán kính \(r = 3\).
b) Ta có:
\({x^2} + {(y + 2)^2} + {z^2} = 1 \Leftrightarrow {(x - 0)^2} + {(y + 2)^2} + {(z - 0)^2} = {1^2}\)
Vậy đây là phương trình mặt cầu có tâm \(I(0; - 2;0)\) và bán kính \(r = 1\).
Trả lời câu hỏi Luyện tập 3 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, viết phương trình mặt cầu \((S)\):
a) Có tâm \(I(2; - 1;0)\) và đi qua điểm \(M(4;1; - 2)\).
b) Có đường kính AB với \(A(0;1;3)\), \(B(4; - 5; - 1)\).
Phương pháp giải:
a)
- Tìm bán kính \(r\) của mặt cầu bằng cách tính khoảng cách IM.
- Sử dụng phương trình mặt cầu với tâm \(I(a;b;c)\) và bán kính \(r\):
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
b)
- Tìm tâm I của mặt cầu là trung điểm của đoạn AB.
- Tính bán kính \(r\) bằng nửa độ dài của AB.
- Dùng phương trình mặt cầu với tâm I và bán kính r.
Lời giải chi tiết:
a)
- Tâm \(I(2; - 1;0)\), điểm \(M(4;1; - 2)\).
- Tính bán kính:
\(r = IM = \sqrt {{{(4 - 2)}^2} + {{(1 + 1)}^2} + {{( - 2 - 0)}^2}} = \sqrt {{2^2} + {2^2} + {{( - 2)}^2}} = \sqrt {4 + 4 + 4} = \sqrt {12} = 2\sqrt 3 .\)
- Phương trình mặt cầu:
\({(x - 2)^2} + {(y + 1)^2} + {z^2} = {(2\sqrt 3 )^2} = 12.\)
Vậy phương trình mặt cầu \(S\) là:
\({(x - 2)^2} + {(y + 1)^2} + {z^2} = 12.\)
b)
- Trung điểm I của đoạn AB là:
\(I = \left( {\frac{{0 + 4}}{2};\frac{{1 - 5}}{2};\frac{{3 - 1}}{2}} \right) = (2; - 2;1).\)
- Tính bán kính \(r\) bằng nửa độ dài AB:
\(r = \frac{{AB}}{2} = \frac{{\sqrt {{{(4 - 0)}^2} + {{( - 5 - 1)}^2} + {{( - 1 - 3)}^2}} }}{2} = \frac{{\sqrt {{4^2} + {{( - 6)}^2} + {{( - 4)}^2}} }}{2} = \frac{{\sqrt {16 + 36 + 16} }}{2} = \frac{{\sqrt {68} }}{2} = \frac{{2\sqrt {17} }}{2} = \sqrt {17} .\)
- Phương trình mặt cầu:
\({(x - 2)^2} + {(y + 2)^2} + {(z - 1)^2} = {(\sqrt {17} )^2} = 17.\)
Vậy phương trình mặt cầu \(S\) là:
\({(x - 2)^2} + {(y + 2)^2} + {(z - 1)^2} = 17.\)
Trả lời câu hỏi Hoạt động 3 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xét mặt cầu S có phương trình:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}\) (1). Khai triển (1), giả sử ta được:
\((1) \Leftrightarrow {x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0.\)
a) Tính A, B, C, D của (2) theo a, b, c, r của (1).
b) Xác định dấu của \({A^2} + {B^2} + {C^2} - D\).
c) Tìm tâm I và bán kính \(r\) của mặt cầu (S) theo A, B, C, D.
Phương pháp giải:
a) Khai triển phương trình mặt cầu và so sánh hệ số với phương trình đã cho.
b) Tính biểu thức \({A^2} + {B^2} + {C^2} - D\) dựa trên các giá trị của A, B, C, và D.
c) Tìm tọa độ tâm và bán kính mặt cầu S bằng cách đưa phương trình về dạng chuẩn.
Lời giải chi tiết:
a)
Khai triển phương trình mặt cầu:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}.\)
Ta có:
\({x^2} - 2ax + {a^2} + {y^2} - 2by + {b^2} + {z^2} - 2cz + {c^2} = {r^2}.\)
Rút gọn, ta được:
\({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + ({a^2} + {b^2} + {c^2} - {r^2}) = 0.\)
So sánh với phương trình đã cho:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0,\)
Suy ra:
\(A = - a,\quad B = - b,\quad C = - c,\quad D = {a^2} + {b^2} + {c^2} - {r^2}.\)
b)
Tính \({A^2} + {B^2} + {C^2} - D\):
\({A^2} + {B^2} + {C^2} - D = {( - a)^2} + {( - b)^2} + {( - c)^2} - ({a^2} + {b^2} + {c^2} - {r^2}).\)
\({A^2} + {B^2} + {C^2} - D = {a^2} + {b^2} + {c^2} - ({a^2} + {b^2} + {c^2}) + {r^2} = {r^2} > 0\)
c)
Từ \(A = - a\), \(B = - b\), \(C = - c\), suy ra:
\(a = - A,\quad b = - B,\quad c = - C.\)
Tọa độ tâm \(I\) của mặt cầu là \(I( - A, - B, - C)\). Bán kính \(r\) của mặt cầu là:
\(r = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)
Vậy, tâm và bán kính của mặt cầu \(S\) là:
\(I( - A, - B, - C),\quad r = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)
Trả lời câu hỏi Luyện tập 4 trang 76 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, xác định tâm I và bán kính \(r\) của mặt cầu có phương trình:
a) \({x^2} + {y^2} + {z^2} + 4x - 2y + 1 = 0\).
b) \(3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y - 9z + 1 = 0\).
Phương pháp giải:
a) Với phương trình mặt cầu dạng tổng quát \({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0\):
- Tìm tọa độ tâm \(I(a,b,c)\) với
\(a = - A\), \(b = - B\), \(c = - C\).
- Tính bán kính \(r = \sqrt {{a^2} + {b^2} + {c^2} - D} \).
b) Nếu phương trình có hệ số khác 1 cho các x^2, y^2, z^2 thì chia cả hai vế cho hệ số đó để đưa về dạng chuẩn.
Lời giải chi tiết:
a) Phương trình mặt cầu:
\({x^2} + {y^2} + {z^2} + 4x - 2y + 1 = 0.\)
So sánh với phương trình mặt cầu tổng quát:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0,\)
ta có:
\(2A = 4 \Rightarrow A = 2,\quad 2B = - 2 \Rightarrow B = - 1,\quad 2C = 0 \Rightarrow C = 0,\quad D = 1.\)
Vậy:
\(a = - A = - 2,\quad b = - B = 1,\quad c = - C = 0.\)
Tâm \(I( - 2,1,0)\). Bán kính:
\(r = \sqrt {{a^2} + {b^2} + {c^2} - D} = \sqrt {{{( - 2)}^2} + {1^2} + {0^2} - 1} = \sqrt {4 + 1 - 1} = \sqrt 4 = 2.\)
Vậy phương trình mặt cầu có tâm \(I( - 2,1,0)\) và bán kính \(r = 2\).
b)
Phương trình mặt cầu:
\(3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y - 9z + 1 = 0.\)
Chia cả hai vế cho \(3\):
\({x^2} + {y^2} + {z^2} + 2x + 4y - 3z + \frac{1}{3} = 0.\)
So sánh với phương trình mặt cầu tổng quát:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0,\)
ta có:
\(2A = 2 \Rightarrow A = 1,\quad 2B = 4 \Rightarrow B = 2,\quad 2C = - 3 \Rightarrow C = - \frac{3}{2},\quad D = \frac{1}{3}.\)
Vậy:
\(a = - A = - 1,\quad b = - B = - 2,\quad c = - C = \frac{3}{2}.\)
Tâm \(I( - 1, - 2,\frac{3}{2})\). Bán kính:
\(r = \sqrt {{a^2} + {b^2} + {c^2} - D} = \sqrt {{{( - 1)}^2} + {{( - 2)}^2} + {{\left( {\frac{3}{2}} \right)}^2} - \frac{1}{3}} = \sqrt {1 + 4 + \frac{9}{4} - \frac{1}{3}} .\)
Tính tiếp:
\(r = \sqrt {\frac{{12 + 48 + 27 - 4}}{{12}}} = \sqrt {\frac{{83}}{{12}}} = \frac{{\sqrt {83} }}{2}.\)
Vậy phương trình mặt cầu có tâm \(I( - 1, - 2,\frac{3}{2})\) và bán kính \(r = \frac{{\sqrt {83} }}{2}\).
Trả lời câu hỏi Vận dụng 1 trang 76 SGK Toán 12 Cùng khám phá
Trong hệ trục Oxyz cho trước (đơn vị trên trục là mét), một trạm thu phát sóng 5G có bán kính vùng phủ sóng của trạm ở ngưỡng 600 m được đặt ở vị trí \(I(200;450;60)\)
a) Lập phương trình mặt cầu mô tả ranh giới bên ngoài và bên trong của vùng phủ sóng.
b) Nếu người dùng điện thoại đang ở vị trí \(A( - 100;50;10)\) thì có thể sử dụng dịch vụ của trạm này không? Vì sao?
Phương pháp giải:
a) Dùng phương trình mặt cầu với tâm I và bán kính \(r\) đã cho.
b) Tính khoảng cách IA và so sánh với bán kính \(r\).
Lời giải chi tiết:
a)
Phương trình mặt cầu với tâm \(I(200;450;60)\) và bán kính \(r = 600\):
\({(x - 200)^2} + {(y - 450)^2} + {(z - 60)^2} = {600^2} = 360000.\)
Vậy phương trình mặt cầu mô tả vùng phủ sóng là:
\({(x - 200)^2} + {(y - 450)^2} + {(z - 60)^2} = 360000.\)
b)
Tính khoảng cách IA:
\(IA = \sqrt {{{( - 100 - 200)}^2} + {{(50 - 450)}^2} + {{(10 - 60)}^2}} = \sqrt {{{( - 300)}^2} + {{( - 400)}^2} + {{( - 50)}^2}} .\)
\(IA = \sqrt {90000 + 160000 + 2500} = \sqrt {252500} \approx 502.5.\)
Vì \(IA \approx 502.5 < 600\), nên người dùng điện thoại ở vị trí \(A( - 100;50;10)\) nằm trong vùng phủ sóng của trạm và có thể sử dụng dịch vụ của trạm này.
Trả lời câu hỏi Vận dụng 2 trang 76 SGK Toán 12 Cùng khám phá
Giả sử người ta biểu diễn mô phỏng của tòa nhà Ericsson Globe ở phần Khởi động trong hệ trục tọa độ Oxyz bởi một mặt cầu có tâm I, đường kính 110 m và \(OA = 85\) m như hình vẽ (đơn vị trên trục là mét). Hãy viết phương trình của mặt cầu này.
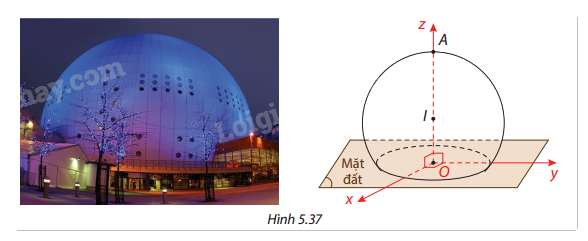
Phương pháp giải:
1. Xác định tọa độ của tâm mặt cầu I:
- Vì tâm mặt cầu nằm trên trục Oz, nên tọa độ của I sẽ có dạng \((0,0,{z_0})\).
- Sử dụng thông tin khoảng cách từ O đến I để tìm \({z_0}\).
2. Viết phương trình của mặt cầu:
- Phương trình tổng quát của mặt cầu có tâm \(I(a,b,c)\) và bán kính \(R\) là:
\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\)
- Thay tọa độ tâm và bán kính vào phương trình trên để hoàn thành lời giải.
Lời giải chi tiết:
1. Xác định tọa độ tâm \(I\):
Do \(OA = 85\) m và bán kính của mặt cầu \(R = \frac{{110}}{2} = 55\) m, nên khoảng cách từ \(O\) đến \(I\) là:
\(OI = OA - R = 85 - 55 = 30 {\rm{m}}\).
Vậy tọa độ của \(I\) là \((0,0,30)\).
2. Viết phương trình của mặt cầu:
Phương trình mặt cầu với tâm \(I(0,0,30)\) và bán kính \(R = 55\) là:
\({(x - 0)^2} + {(y - 0)^2} + {(z - 30)^2} = {55^2}\)
\( \Leftrightarrow{x^2} + {y^2} + {(z - 30)^2} = 3025\).
Mục 2 của SGK Toán 12 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp hướng dẫn chi tiết, từng bước giải các bài tập trang 74, 75, 76, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài.
Để cung cấp nội dung chính xác, cần biết mục 2 thuộc chương nào. Tuy nhiên, dưới đây là một số chủ đề thường gặp:
Bài 1: (Ví dụ, giả sử bài tập yêu cầu tính đạo hàm của hàm số y = sin(2x)).
Lời giải:
y' = cos(2x) * 2 = 2cos(2x)
Bài 2: (Ví dụ, giả sử bài tập yêu cầu tìm cực trị của hàm số y = x^3 - 3x + 2).
Lời giải:
Bài 3: (Ví dụ, giả sử bài tập yêu cầu tìm giá trị lớn nhất của hàm số y = -x^2 + 4x - 1 trên đoạn [0; 3]).
Lời giải:
Tìm điểm cực trị: y' = -2x + 4 = 0 => x = 2. x = 2 thuộc đoạn [0; 3].
Tính giá trị hàm số tại các điểm đầu mút và điểm cực trị: y(0) = -1, y(2) = 3, y(3) = -1.
Vậy giá trị lớn nhất của hàm số trên đoạn [0; 3] là 3.
Bài 4: (Ví dụ, giả sử bài tập yêu cầu viết phương trình đường thẳng đi qua điểm A(1; 2) và vuông góc với đường thẳng d: x + y - 3 = 0).
Lời giải:
Đường thẳng d có vectơ pháp tuyến n = (1; 1). Đường thẳng cần tìm có vectơ chỉ phương là n = (1; 1).
Phương trình đường thẳng cần tìm là: (x - 1) + (y - 2) = 0 => x + y - 3 = 0.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập mục 2 trang 74, 75, 76 SGK Toán 12 tập 2 một cách hiệu quả. Chúc các em học tập tốt!