Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 44 SGK Toán 12 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài giải này được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với chương trình học.
Cho hàm số \(y = f(x) = {x^3} - 3{x^2} + 3\) a) Sử dụng phần mềm GeoGebra vẽ đồ thị (C) của hàm số đã cho. b) Tìm nghiệm gần đúng (làm tròn đến hàng phần trăm) của phương trình \(f(x) = 0\) c) Dựa vào đồ thị đã vẽ ở câu a, biện luận theo tham số m số nghiệm của phương trình \({x^3} - 3{x^2} + 3 = m\).
Đề bài
Trả lời câu hỏi Luyện tập 2 trang 44 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = {x^3} - 3{x^2} + 3\)
a) Sử dụng phần mềm GeoGebra vẽ đồ thị (C) của hàm số đã cho.
b) Tìm nghiệm gần đúng (làm tròn đến hàng phần trăm) của phương trình \(f(x) = 0\)
c) Dựa vào đồ thị đã vẽ ở câu a, biện luận theo tham số m số nghiệm của phương trình \({x^3} - 3{x^2} + 3 = m\).
Phương pháp giải - Xem chi tiết
a) Mở GeoGebra và nhập hàm số f(x).
b) Sử dụng câu lệnh Nghiem( Đa thức ) để tìm các nghiệm gần đúng.
c)
- Tạo thanh trượt m và vẽ hàm số y = m
- Quan sát và biện luận
Lời giải chi tiết
a)
- Mở GeoGebra và nhập hàm số \(f(x) = {x^3} - 3{x^2} + 3\)
- Đồ thị của hàm số sẽ trông như sau:
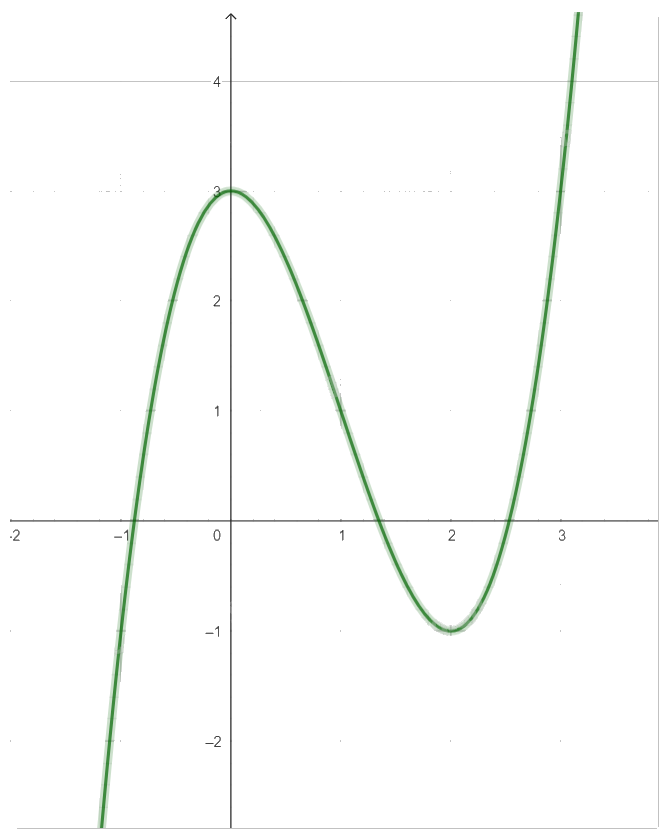
b) Sử dụng câu lệnh Nghiem(Đa thức) để tìm các điểm mà đồ thị cắt trục x sẽ ra được kết quả như sau:

Từ đó, ta thấy phương trình \(f(x) = 0\) có các nghiệm là: \({x_1} \approx - 0.88,{x_2} \approx 1.35,{x_3} \approx 2.53\)
c)
- Tạo thanh trượt m với m nằm trong khoảng (-5,5)
- Vẽ đồ thị hàm số y = m
- Số giao điểm của hai đồ thị sẽ là nghiệm của phương trình \({x^3} - 3{x^2} + 3 = m\)(*)
- Kéo thanh trượt m ta sẽ thấy sự thay đổi của các nghiệm
Với \(m > 3\), phương trình (*) có 1 nghiệm.
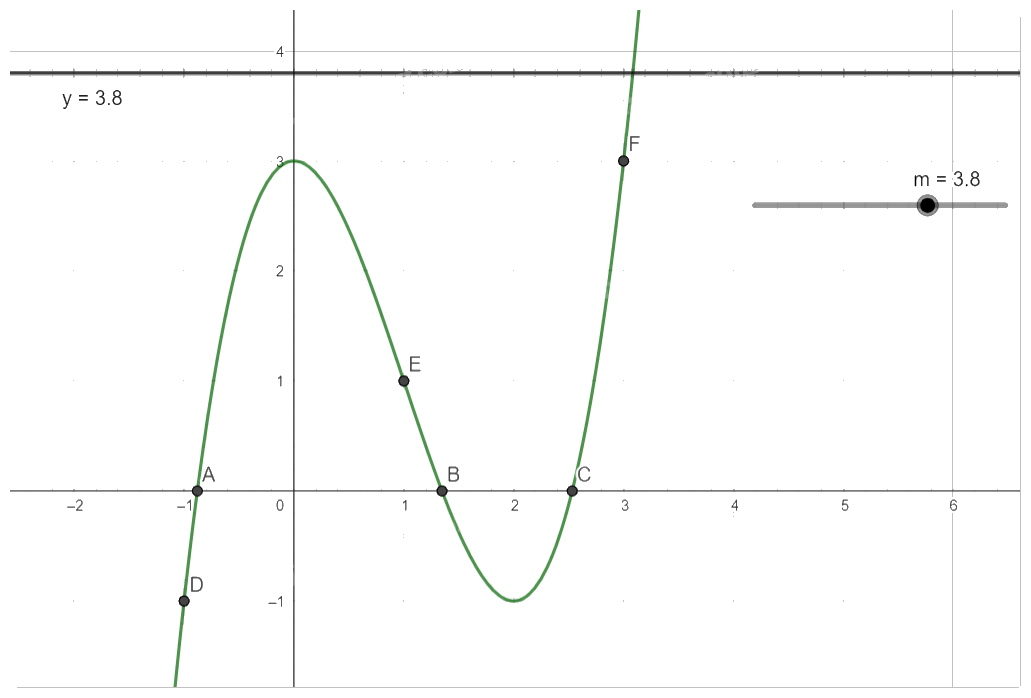
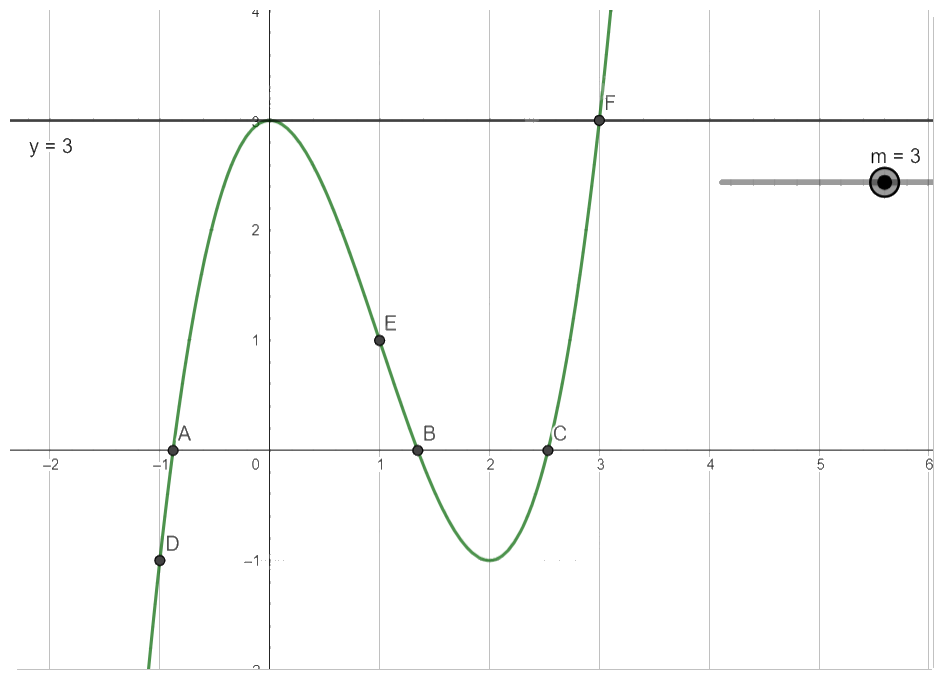
Với \(m = 3\), phương trình (*) có 2 nghiệm.
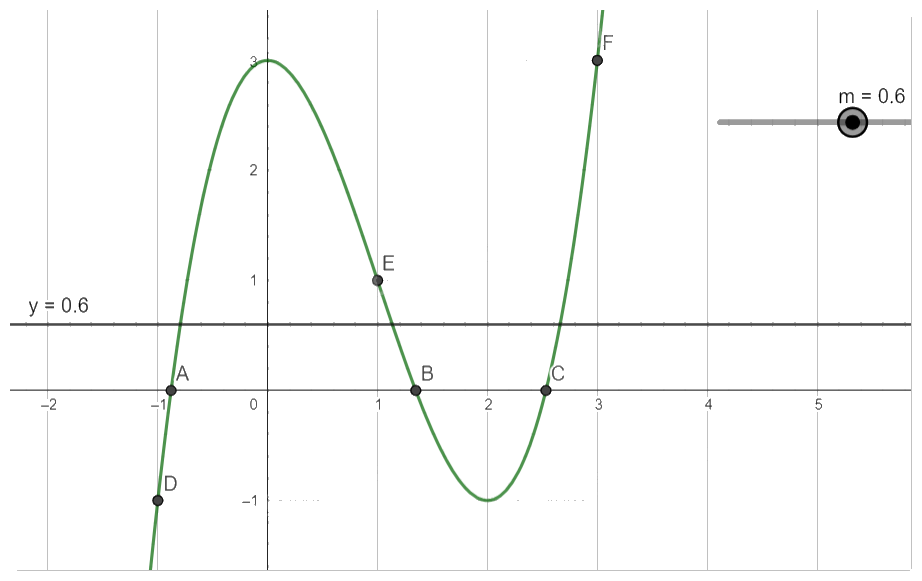
Với \( - 1 < m < 3\), phương trình (*) có 3 nghiệm phân biệt.
Với \(m = - 1\), phương trình (*) có 2 nghiệm.
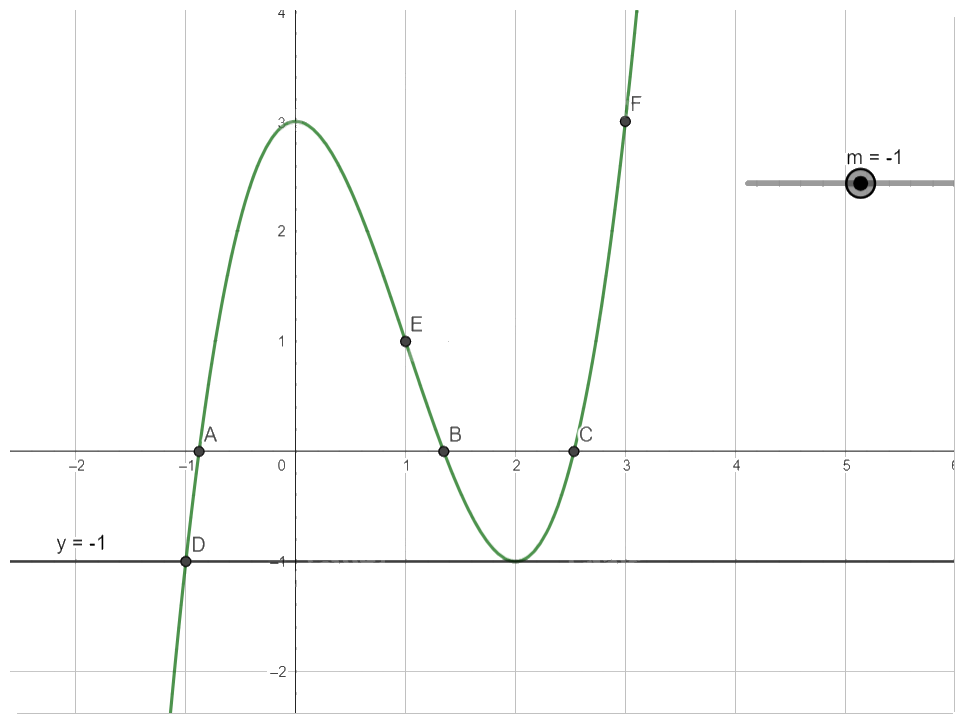
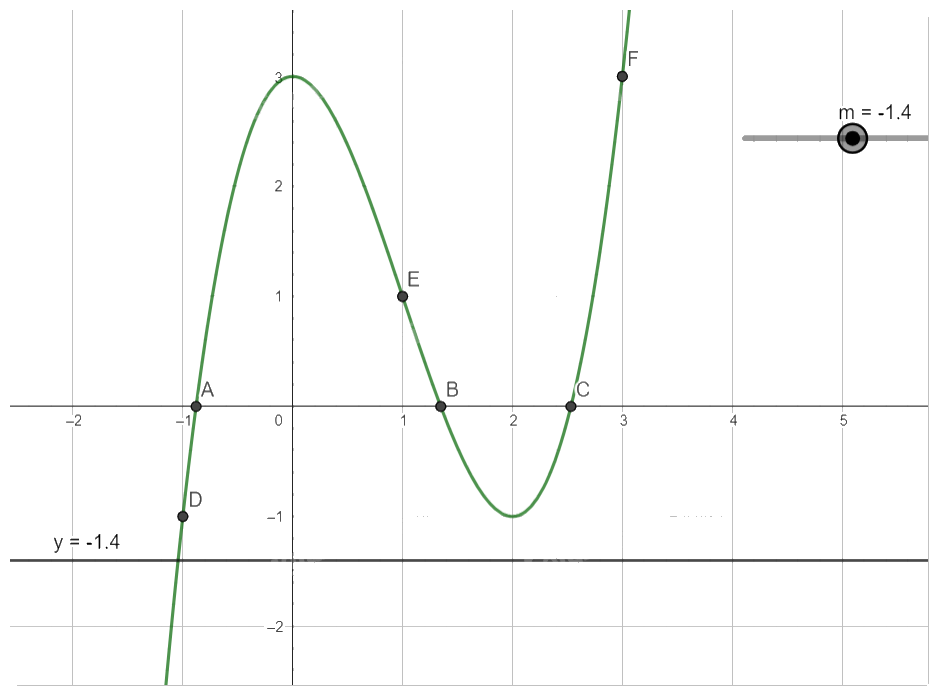
Với \(m < - 1\), phương trình (*) có 1 nghiệm.
Mục 2 trang 44 SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học Toán 12 và chuẩn bị cho kỳ thi THPT Quốc gia.
Để giải quyết các bài tập trong mục này, học sinh cần hiểu rõ các khái niệm và quy tắc sau:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 44 SGK Toán 12 tập 1:
Giải:
f'(x) = 3x2 + 4x - 5
Giải:
f'(x) = 2cos(2x)
Giải:
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
Xét dấu f'(x) trên các khoảng (-∞, 0), (0, 2), (2, +∞), ta thấy:
Vậy hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2.
Để học tốt môn Toán 12 và đạt kết quả cao trong kỳ thi THPT Quốc gia, học sinh nên:
Việc giải bài tập Mục 2 trang 44 SGK Toán 12 tập 1 đòi hỏi sự nắm vững kiến thức về đạo hàm và các quy tắc tính đạo hàm. Hy vọng với hướng dẫn chi tiết và các mẹo học tập trên, các em học sinh sẽ tự tin giải quyết các bài tập và đạt kết quả tốt trong môn Toán 12.