Chào mừng các em học sinh đến với bài giải bài tập 3.4 trang 95 SGK Toán 12 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả. Hãy cùng khám phá và chinh phục bài toán này nhé!
Một ngân hàng thống kê ở bảng dưới số tiền mà khách hàng rút từ một máy ATM (máy rút tiền tự động) trong một buổi sáng.
Đề bài
Một ngân hàng thống kê ở bảng dưới số tiền mà khách hàng rút từ một máy ATM (máy rút tiền tự động) trong một buổi sáng.
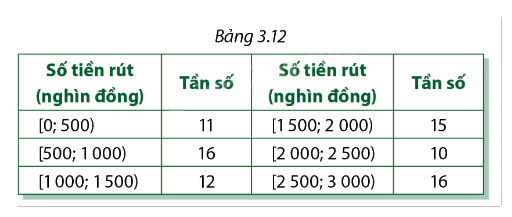
Tìm khoảng tứ phân vị của số tiền rút (làm tròn kết quả đến hàng đơn vị). Nêu ý nghĩa của các kết quả tìm được.
Phương pháp giải - Xem chi tiết
- Tính tổng số lần rút tiền.
- Tìm các tứ phân vị \({Q_1},{Q_3}\)
- Tìm khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\)
Lời giải chi tiết
- Tổng số lần rút tiền: N = 11 + 16 + 12 + 15 + 10 +16 = 80
- Tứ phân vị:
\(\frac{N}{4} = 20\) rơi vào nhóm [500; 1000)
\({Q_1} = 500 + \frac{{20 - 11}}{{16}}.500 = 781\)
\(\frac{{3N}}{4} = 60\) rơi vào nhóm [2000; 2500)
\({Q_3} = 2000 + \frac{{60 - 54}}{{10}}.500 \approx 2300\)
- Khoảng tứ phân vị:
\({\Delta _Q} = {Q_3} - {Q_1} = 2300 - 781 \approx 1519\)nghìn đồng
- Khoảng tứ phân vị cho thấy mức độ phân tán của số tiền rút. Kết quả của khoảng tứ phần vị chỉ ra rằng số tiền rút ra tương đối đồng đều.
Bài tập 3.4 trang 95 SGK Toán 12 tập 1 thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tìm cực trị của hàm số, khảo sát hàm số, hoặc giải các bài toán tối ưu hóa. Để giải quyết bài tập này một cách hiệu quả, các em cần nắm vững các bước sau:
Ví dụ minh họa:
Giả sử bài tập 3.4 yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
Các dạng bài tập thường gặp:
Lưu ý khi giải bài tập:
Mở rộng kiến thức:
Ngoài việc giải bài tập 3.4 trang 95 SGK Toán 12 tập 1, các em có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong các lĩnh vực khác nhau, chẳng hạn như vật lý, kinh tế, hoặc khoa học máy tính. Việc mở rộng kiến thức sẽ giúp các em hiểu sâu hơn về môn Toán và có thể áp dụng kiến thức vào thực tế.
Tổng kết:
Bài tập 3.4 trang 95 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt nhất. Chúc các em học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
| y = tanx | y' = 1/cos2x |